并查集详解
并查集详解
- 什么是并查集?
- 并查集的基本操作
-
- 初始化
- 查找根结点
- 查询两个结点是否同根
- 合并
- 并查集的优化
-
- 优化1:避免退化(按秩合并)
- 优化2:路径压缩
- 复杂度分析
- 最终代码实现
- 例题
什么是并查集?
并查集集是一种维护集合的数据结构,它的名字中 “并”、“查”、“集” 分别取自 Union(合并)、Find(查找)、Set(集合)这 3 个单词。
也就是说,并查集支持下面两个操作:
- 合并:合并两个集合。
- 查找:判断两个元素是否在一个集合。
那么并查集是用什么实现的呢?
其实就是用一个数组:
int father[n];
其中 father[i] 表示元素 i 的父亲结点,而父亲结点本身也是这个集合内的元素。
例如 father[1] = 2 就表示元素 1 的父亲结点是元素 2 ,以这种父系关系来表示元素所属的集合。
另外,如果 father[i] = i ,则说明元素 i 是该集合的根结点,但对同一个集合来说只存在一个根结点,且将其作为所属集合的标识。
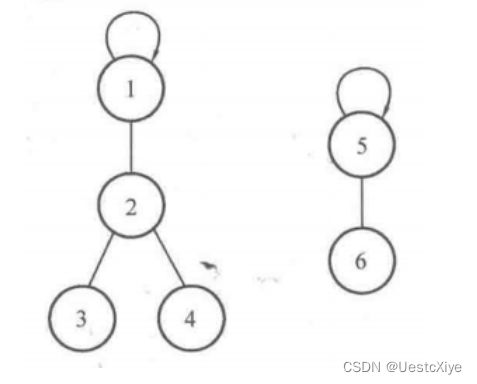
举个例子,下面给出了上图的 father 数组情况。
father[1] = 1; // 1 的父亲结点是自己,也就是说 1 号是根结点
father[2] = 1; // 2 的父亲结点是 1
father[3] = 2; // 3 的父亲结点是 2
father[4] = 2; // 4 的父亲结点是 2
father[5] = 5; // 5 的父亲结点是自己,也就是说 5 号是根结点
father[6] = 5; // 6 的父亲结点是 5
我们发现有这样的规律:
father[i] = 1 说明元素 1 的父亲结点是自己,即元素 1 是集合的根结点。
father[2] = 1 说明元素 2 的父亲结点是元素 1 ,
father[3] = 2 和 father[4] = 2 说明元素 3 和 元素 4 的父亲结点都是元素 2 ,
这样元素 1、2、3、4 就在同一个集合当中。
fathe[5] = 5 和 father[6] = 5 则说明 5 和 6 是以 5 为根结点的集合。
这样就得到了两个不同的集合。
并查集的基本操作
总体来说,并查集的使用需要先初始化 father 数组,然后再根据需要进行查找或合并的操作。
初始化
一开始,每个元素都是独立的一个集合,因此需要令所有 father[i] 等于 i :
void init()
{
// iota函数可以把数组初始化为 0 到 n-1
iota(father.begin(), father.end(), 0);
}
查找根结点
由于规定同一个集合中只存在一个根结点,因此查找操作就是对给定的结点寻找其根结点的过程。
实现的方式可以是迭代或是递归,但是其思路都是一样的,即反复寻找父亲结点,直到找到根结点(即 father[i] = i 的结点)。
迭代:
int find(int x)
{
while (x != father[x])
{
// 路径压缩,使得下次查找更快
father[x] = father[father[x]];
x = father[x];
}
return x;
}
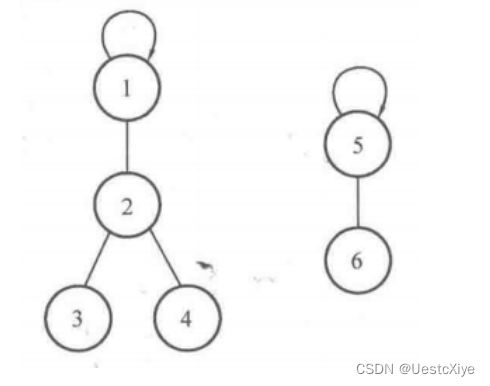
以上图为例,要查找元素 4 的根结点是谁,应按照上面的递推方法,流程如下:
-
x = 4 , father[4] = 2,因此 4 != father[4],于是继续查;
-
x = 2, father[2] = 1,因此 2 != father[2],于是继续查;
-
x = 1, father[1] = 1,因此 1 = father[1] ,找到根结点,返回 1 。
当然,这个过程也可以用递归来实现:
int find(int x)
{
if (x == father[x])
return x; // 如果找到根结点,则返回根结点编号x
else
return find(father[x]); // 否则,递归判断 x 的父亲结点是否是根结点
}
递归(one line code):
int find(int x)
{
return father[i] == i ? father[i] : find(father[i]);
}
查询两个结点是否同根
当我们要查询两个元素是否属于同一个组时,我们需要沿着各个节点往上向树的根进行查询,如果最终发现两个元素的根相同,那么他们就属于同一个组。反之,则不属于同一个组。
代码如下所示:
bool isConnected(int p, int q)
{
return find(p) == find(q);
}
合并
合并是指把两个集合合并成一个集合,题目中一般给出两个元素,要求把这两个元素所在的集合合并。
具体实现上一般是先判断两个元素是否属于同一个集合,只有当两个元素属于不同集合时才合并,而合并的过程一般是把其中一个集合的根结点的父亲指向另一个集合的根结点。
于是思路就比较清晰了,主要分为以下两步:
-
对于给定的两个元素 a、b,判断它们是否属于同一集合。可以调用上面的查找函数,对这两个元素 a、b 分别查找根结点,然后再判断其根结点是否相同。
-
合并两个集合:在 步骤1 中已经获得了两个元素的根结点 faA 与 faB ,因此只需要把其中一个的父亲结点指向另一个结点。例如可以令 father[faA] = faB,当然反过来令 father[faB] = faA 也是可以的,两者没有区别。
还是以下图为例:
把元素 4 和元素 6 合并,过程如下:
-
判断元素 4 和元素 6 是否属于同一个集合:元素 4 所在集合的根结点是 1 ,元素 6 所在集合的根结点是 5 ,因此它们不属于同一个集合。
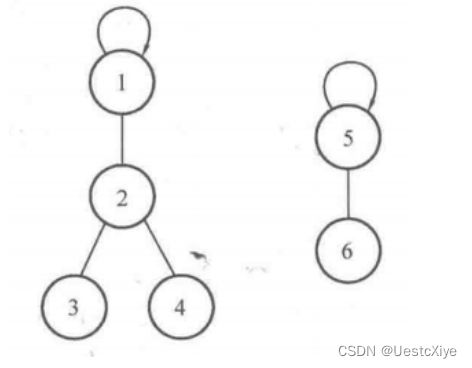
-
合并两个集合:令 father[5] = 1 ,即把元素 5 的父亲设为元素 1 。
于是有了合并后的集合,如图所示:
现在可以写出合并的代码了:
void connect(int a, int b)
{
int faA = find(a); // 查找 a 的根结点,记为 faA
int faB = find(b); // 查找 b 的根结点,记为 faB
if (faA != faB)
{
// 如果不属于同一个集合
father[faA] = faB; // 合并它们
}
}
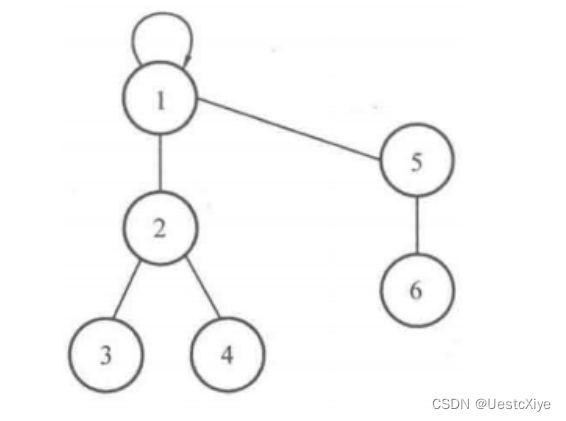
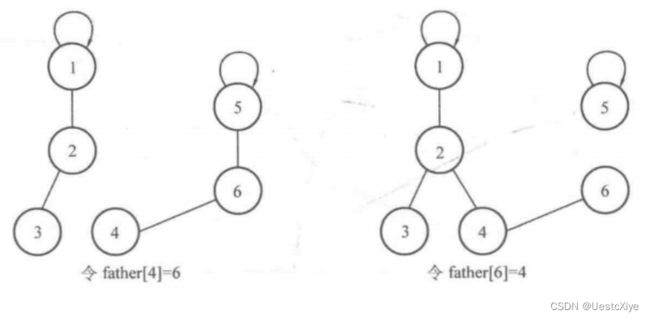
这里需要注意的是,很多初学者会直接把其中一个元素的父亲设为另一个元素,即直接令 father[a]=b 来进行合并,这并不能实现将集合合并的效果。
例如,将上面例子中的 father[4] 设为 6 ,或是把 father[6] 设为 4 ,就不能实现集合合并的效果,如图所示。
因此,初学者使用上面给出的 connect 函数来进行合并操作。
最后说明并查集的一个性质。在合并的过程中,只对两个不同的集合进行合并,如果两个元素在相同的集合中,那么就不会对它们进行操作。这就保证了在同一个集合中一定不会产生环,即并查集产生的每一个集合都是一棵树。
并查集的优化
优化1:避免退化(按秩合并)
因为并查集的结构是树状结构,所以需注意退化问题。避免退化发生的方法如下:
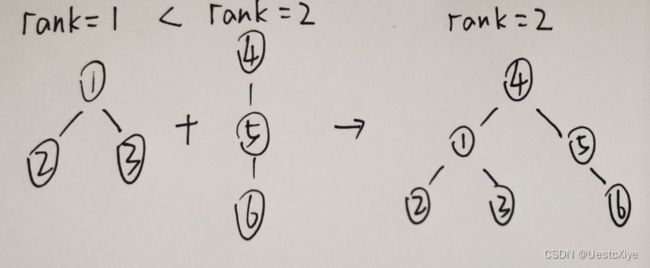
首先,我们合并时,可记录这棵树的高度(记为 size)。
接下来当我们需合并两棵树时,我们先对两棵树的高度进行判断,如不同,则让高度小的树的根指向高度大的根。如下图:
优化代码如下所示:
void init()
{
// iota函数可以把数组初始化为 0 到 n-1
iota(father.begin(), father.end(), 0);
for (int i = 0; i < size.size(); i++)
size[i] = 1;
}
void connect(int p, int q)
{
int i = find(p), j = find(q);
if (i != j)
{
// 按秩合并:每次合并都把深度较小的集合合并在深度较大的集合下面
if (size[i] < size[j])
{
father[i] = j;
size[j] += size[i];
}
else
{
father[j] = i;
size[i] += size[j];
}
}
}
优化2:路径压缩
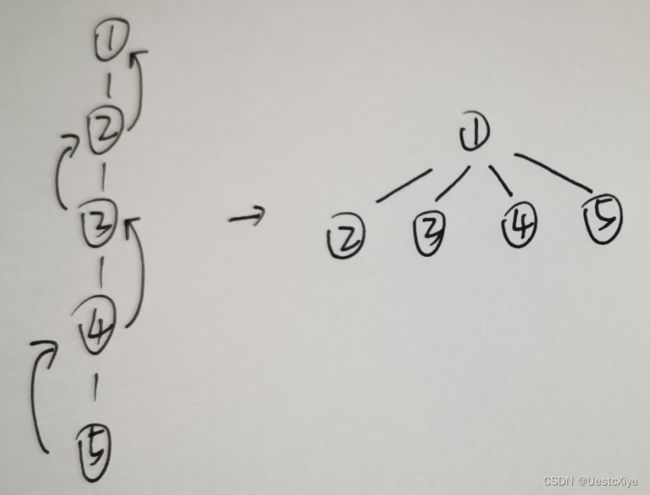
由于查询时我们需沿着元素所在的树从下往上查询,最终找到这棵树的根,表明这个元素与其根对应元素属于同一组。
因为在此查询过程中我们会经过许多节点,而如果我们能将这个元素直接指向根节点,那么就能节省许多查询的时间。
同时,在查询过程中,每次经过的节点,我们都可以同时将他们一起直接指向根节点。这样做的话,我们再查询这些节点时,就能很快知道他们的根是谁了。
迭代:
int find(int x)
{
while (x != father[x])
{
// 路径压缩,使得下次查找更快
father[x] = father[father[x]];
x = father[x];
}
return x;
}
递归:
int find(int x)
{
if (x == father[x])
return x; // 如果找到根结点,则返回根结点编号x
else
{
// 使元素直接指向树的根
father[x] = find(father[x]);
return find(father[x]); // 否则,递归判断 x 的父亲结点是否是根结点
}
}
递归(one line code):
int find(int x)
{
// 使元素直接指向树的根
return father[x] == x ? father[x] : father[x] = find(father[x]);
}
复杂度分析
经过两个优化后,并查集的效率变得非常高。
对n个元素的并查集进行一次操作的均摊复杂度是O(α(n)) (α(n)是阿克曼函数的反函数,α(n) 可以认为是一个很小的常数),比优化前的O(log(n))还要快。
最终代码实现
class UnionFind
{
vector<int> father, size;
public:
UnionFind(int n) : father(n), size(n) {}
void init()
{
// iota函数可以把数组初始化为 0 到 n-1
iota(father.begin(), father.end(), 0);
for (int i = 0; i < size.size(); i++)
size[i] = 1;
}
int find(int x)
{
while (x != father[x])
{
// 路径压缩,使得下次查找更快
father[x] = father[father[x]];
x = father[x];
}
return x;
}
void connect(int p, int q)
{
int i = find(p), j = find(q);
if (i != j)
{
// 按秩合并:每次合并都把深度较小的集合合并在深度较大的集合下面
if (size[i] < size[j])
{
father[i] = j;
size[j] += size[i];
}
else
{
father[j] = i;
size[i] += size[j];
}
}
}
bool isConnected(int p, int q)
{
return find(p) == find(q);
}
};
init 函数可以省略:
class UnionFind
{
vector<int> father, size;
public:
UnionFind(int n) : father(n), size(n, 1)
{
// iota函数可以把数组初始化为 0 到 n-1
iota(father.begin(), father.end(), 0);
}
int find(int x)
{
while (x != father[x])
{
// 路径压缩,使得下次查找更快
father[x] = father[father[x]];
x = father[x];
}
return x;
}
void connect(int p, int q)
{
int i = find(p), j = find(q);
if (i != j)
{
// 按秩合并:每次合并都把深度较小的集合合并在深度较大的集合下面
if (size[i] < size[j])
{
father[i] = j;
size[j] += size[i];
}
else
{
father[j] = i;
size[i] += size[j];
}
}
}
bool isConnected(int p, int q)
{
return find(p) == find(q);
}
};
例题
Leetcode684. 冗余连接