LeetCode第224场周赛
LeetCode第224场周赛
题目:1725. 可以形成最大正方形的矩形数目
给你一个数组 rectangles ,其中 rectangles[i] = [li, wi] 表示第 i 个矩形的长度为 li 、宽度为 wi 。
如果存在 k 同时满足 k <= li 和 k <= wi ,就可以将第 i 个矩形切成边长为 k 的正方形。例如,矩形 [4,6] 可以切成边长最大为 4 的正方形。
设 maxLen 为可以从矩形数组 rectangles 切分得到的 最大正方形 的边长。
返回可以切出边长为 maxLen 的正方形的矩形 数目 。
示例 1:
输入:rectangles = [[5,8],[3,9],[5,12],[16,5]]
输出:3
解释:能从每个矩形中切出的最大正方形边长分别是 [5,3,5,5] 。
最大正方形的边长为 5 ,可以由 3 个矩形切分得到。
示例 2:
输入:rectangles = [[2,3],[3,7],[4,3],[3,7]]
输出:3
提示:
1 <= rectangles.length <= 1000
rectangles[i].length == 2
1 <= li, wi <= 109
li != wi
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/number-of-rectangles-that-can-form-the-largest-square
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
代码:
一个矩形能被切成的最大正方形的边长取决于它的小边,所以两次遍历,第一次找出可以切成的最大正方形的边长,第二次遍历统计最大正方形的个数。
class Solution {
public int countGoodRectangles(int[][] rectangles) {
int n = rectangles.length;
int[] a = new int[n];
for(int i = 0; i < n; i++) a[i] = Math.min(rectangles[i][0], rectangles[i][1]);
Arrays.sort(a);
int ans = 0;
for(int i = n - 1; i > -1 && a[i] == a[n - 1]; i--) ans++;
return ans;
}
}
题目:1726. 同积元组
给你一个由 不同 正整数组成的数组 nums ,请你返回满足 a * b = c * d 的元组 (a, b, c, d) 的数量。其中 a、b、c 和 d 都是 nums 中的元素,且 a != b != c != d 。
示例 1:
输入:nums = [2,3,4,6]
输出:8
解释:存在 8 个满足题意的元组:
(2,6,3,4) , (2,6,4,3) , (6,2,3,4) , (6,2,4,3)
(3,4,2,6) , (4,3,2,6) , (3,4,6,2) , (4,3,6,2)
示例 2:
输入:nums = [1,2,4,5,10]
输出:16
解释:存在 16 个满足题意的元组:
(1,10,2,5) , (1,10,5,2) , (10,1,2,5) , (10,1,5,2)
(2,5,1,10) , (2,5,10,1) , (5,2,1,10) , (5,2,10,1)
(2,10,4,5) , (2,10,5,4) , (10,2,4,5) , (10,2,4,5)
(4,5,2,10) , (4,5,10,2) , (5,4,2,10) , (5,4,10,2)
示例 3:
输入:nums = [2,3,4,6,8,12]
输出:40
示例 4:
输入:nums = [2,3,5,7]
输出:0
提示:
1 <= nums.length <= 1000
1 <= nums[i] <= 104
nums 中的所有元素 互不相同
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/tuple-with-same-product
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
代码:
现予处理两个数组合的所有可能性用哈希表存每个乘积的个数。然后再将所有数配对。
class Solution {
public int tupleSameProduct(int[] nums) {
HashMap<Integer, Integer> map = new HashMap<>();
int n = nums.length;
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
if(i == j) continue;
map.put(nums[i] * nums[j], map.getOrDefault(nums[i] * nums[j], 0) + 1);
}
}
int ans = 0;
for(int i = 0; i < n; i++) {
for(int j = i + 1; j < n; j++) {
int a = map.get(nums[i] * nums[j]) - 2;
ans += Math.max(a, 0) * 2;
}
}
return ans;
}
}
题目:1727. 重新排列后的最大子矩阵
给你一个二进制矩阵 matrix ,它的大小为 m x n ,你可以将 matrix 中的 列 按任意顺序重新排列。
请你返回最优方案下将 matrix 重新排列后,全是 1 的子矩阵面积。
示例 1:
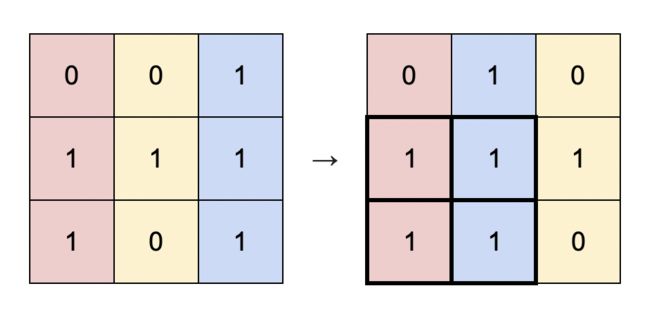
输入:matrix = [[0,0,1],[1,1,1],[1,0,1]]
输出:4
解释:你可以按照上图方式重新排列矩阵的每一列。
最大的全 1 子矩阵是上图中加粗的部分,面积为 4 。
示例 2:
输入:matrix = [[1,0,1,0,1]]
输出:3
解释:你可以按照上图方式重新排列矩阵的每一列。
最大的全 1 子矩阵是上图中加粗的部分,面积为 3 。
示例 3:
输入:matrix = [[1,1,0],[1,0,1]]
输出:2
解释:由于你只能整列整列重新排布,所以没有比面积为 2 更大的全 1 子矩形。
示例 4:
输入:matrix = [[0,0],[0,0]]
输出:0
解释:由于矩阵中没有 1 ,没有任何全 1 的子矩阵,所以面积为 0 。
提示:
m == matrix.length
n == matrix[i].length
1 <= m * n <= 105
matrix[i][j] 要么是 0 ,要么是 1 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/largest-submatrix-with-rearrangements
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
代码:
这道题与LeetCode第85题最大矩阵很像。
最大矩阵是用单调栈做的,这道题题目中给出可以任意交换两列,所以我们可以直接按升序排序后处理,然后遍历,以当前列的数为高,因为它后面的数都比它大所以他的宽是 m - i (m :列数 i :当前列),然后统一收集一下最大面积。
class Solution {
public int largestSubmatrix(int[][] matrix) {
int n = matrix.length, m = matrix[0].length;
for (int i = 1; i < n; i++) {
for (int j = 0; j < m; j++) {
if (matrix[i][j] != 0) {
matrix[i][j] += matrix[i - 1][j];
}
}
}
int ans = 0;
int[] a = new int[m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
a[j] = matrix[i][j];
}
Arrays.sort(a);
for (int j = 0; j < m; j++)
ans = Math.max(ans, a[j] * (m - j));
}
return ans;
}
}