机器学习之决策树
1. 引入
顾名思义, 决策树是由一个个“决策”所组成的树, 放“决策依据”的是非叶结点, 放“决策结果”的是叶结点. 决策树是一种简单高效并且具有强解释性的模型, 它也是我们人类在面临决策问题时一种很自然的处理机制.
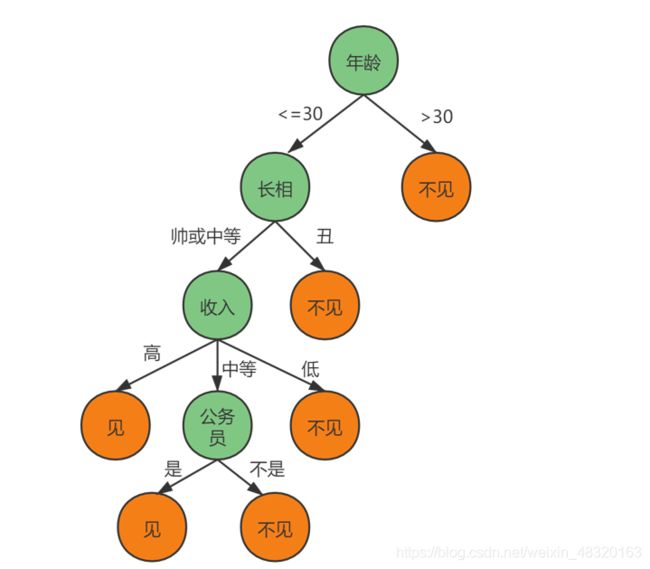
比如, 一位母亲要给她的女儿介绍男朋友, 可能就有这样一段对话:
女儿: 多大年纪了?
母亲: 26.
女儿: 长得如何?
母亲: 挺帅一小伙.
女儿: 收入高不?
母亲: 不算很高, 中等水平.
女儿: 是公务员不?
母亲: 是, 在税务局上班.
女儿: 那好, 我去看看.
整段对话看来, 其实就是一个决策问题的处理过程. 决策结果也很简单, “见”或者“不见”. 女儿经过一系列的问询, 最终作出的结果是“见”. 这在计算机中,我们可以把它看作是许多个"if-then"操作. 若满足条件(condition), 就执行操作.
决策树可以看作是一个装着“if-then"规则的集合, 由决策树的根节点到叶结点的每一条路径, 构建一条规则: 路径上内部结点的特征对应着规则的条件, 叶结点对应规则的结论. 决策树的“if-then”规则集合有一个重要性质: 互斥并且完备. 也就是说, 每个实例都被一条规则(路径)所覆盖, 并且只被这一条规则覆盖.
决策树学习的本质, 是从训练数据集中归纳出一组“if-then”的分类规则. 与训练集不相矛盾的决策树, 可能有很多个, 也可能一个也没有, 所以我们需要选择一个与训练数据集矛盾较小的决策树; 另一方面, 我们可以把决策树看成一个条件概率模型, 我们的目标是将实例分配到条件概率更大的那一类中去.
其基本流程遵循简单且直观的“分而治之”(divide-and-conquer)策略, 如下所示:
输入: 训练集\(\mathbf{D} = \{(x_1, y_1), (x_2, y_2),\dots,(x_n, y_n)\};\)
属性集\(\mathbf{A} = \{a_1, a_2,\dots,a_m\}.\)
过程: 函数 \(\rm TreeGenerate(\mathbf{D}, \mathbf{A})\)
1: 生成结点 \(\rm node\).
2: \(\rm if\) \(\mathbf{D}\)中样本全属于同一类别\(\mathbf{C}\) \(\rm then\)
3: 将\(\rm node\)标记为\(\mathbf{C}\)类叶结点; \(\rm return\)4: \(\rm end\) \( \rm if\)
5: \(\rm if\) \(\mathbf{A} = \emptyset \) \(\rm or\) \(\mathbf{D}\)中样本在\(\mathbf{A}\)上取值相同 \(\rm then\)
6: 将\(\rm node\)标记为叶结点, 其类别标记为\(\mathbf{D}\)中样本数最多的类; \(\rm return\)
7: \(\rm end\) \( \rm if\)
8: 从\(\mathbf{A}\)中选择最优划分属性\(a_*\);
9: \(\rm for\) \(a_*\)的每一个值\(a_*^{v}\) \(\rm do\)
10: 为\(\rm node\) 生成一个分支; 令\(\mathbf{D}_v\)表示在\(\mathbf{D}\)中在\(a_*\)上取值为\(a_*^{v}\)的样本子集;
11: \(\rm if\) \(\mathbf{D}_v\)为空 \(\rm then \)
12: 将分支结点标记为叶结点, 其类别标记为\(\mathbf{D}\)中样本最多的类; \(\rm return\)
13: \(\rm else\)
14: 以\(\rm TreeGenerate(\mathbf{D}_v, \mathbf{A} \backslash \{a_*\})\)为分支结点
15: \(\rm end\) \( \rm if\)
16: \(\rm end\) \( \rm for\)
输出: 以\(\rm node\)为根节点的一颗决策树
2. ID3算法
信息熵(information entropy): 信息量大小的度量, 即表示随机变量不确定性的度量, 是度量样本集合纯度最常用的一种指标. 假定当前样本集合\(\mathbf{D}\)中第\(i\)类样本所占比例为\(p_i\)(\(i=1, 2,\dots, m)\), 则\(\mathbf{D}\)的信息熵定义为:
$$Ent(\mathbf{D})= - \sum_{i=1}^m p_i \log_2 p_i$$
\(Ent(\mathbf{D})\)的值越小, 则\(\mathbf{D}\)的纯度越高.
假定离散属性\(a\)有\(V\)个可能的取值\(\{a^1, a^2,\dots, a^V\}\), 若使用\(a\)来对样本集\(\mathbf{D}\)进行划分, 则会产生\(V\)个分支结点, 其中第\(v\)个分支结点包含了\(\mathbf{D}\)中所有在属性\(a\)上取值为\(a^v\)的样本, 记为\(\mathbf{D}^v\). 我们可根据上面的式子计算出\(\mathbf{D}^v\)的信息熵, 再考虑到不同的分支结点所包含的样本数不同, 给分支结点赋予权重\(|\mathbf{D}^v| / |\mathbf{D}\) , 即样本数越多的分支结点的影响越大, 于是看计算出用属性\(a\)对样本集\(\mathbf{D}\)进行划分所获得的“信息增益”(information gain):
$$Gain(\mathbf{D}, a) = Ent(\mathbf{D}) - \sum_{v=1}^V \frac {|\mathbf{D}^v|}{|\mathbf{D}|} Ent(\mathbf{D}^v)$$
ID3算法就是选择的\( \arg \max Gain(\mathbf{D}, a)\)来进行属性的划分.
下面举一个例子:
| Day | Outlook | Temperature | Humidity | Wind | Play |
|---|---|---|---|---|---|
| 1 | Sunny | Hot | High | Weak | No |
| 2 | Sunny | Hot | High | Strong | No |
| 3 | Overcast | Hot | High | Weak | Yes |
| 4 | Rain | Mild | High | Weak | Yes |
| 5 | Rain | Cool | Normal | Weak | Yes |
| 6 | Rain | Cool | Normal | Strong | No |
| 7 | Overcast | Cool | Normal | Strong | Yes |
| 8 | Sunny | Mild | High | Weak | No |
| 9 | Sunny | Cool | Normal | Weak | Yes |
| 10 | Rain | Mild | Normal | Weak | Yes |
| 11 | Sunny | Mild | Normal | Strong | Yes |
| 12 | Overcast | Mild | High | Strong | Yes |
| 13 | Overcast | Hot | Normal | Weak | Yes |
| 14 | Rain | Mild | High | Strong | No |
4个条件属性: Outlook, Temperature, Humidity, Wind.
1个决策属性: Play(y or n).
那么我们首先可计算出根结点的信息熵:
\(Ent(\mathbf{D})=-\sum_{i=1}^2 p_i \log_2 p_i = -(\frac {5}{14}\log_2\frac {5}{14}+\frac {9}{14}\log_2\frac {9}{14})=0.9401\)
然后, 我们要计算出当前属性集合{Outlook, Temperature, Humidity, Wind}中每个属性的信息增益.以“Outlook”为例, 它有3个可能的取值: {Sunny, Overcast, Rain}. 若使用该属性对\(\mathbf{D}\)进行划分, 则可得到3个子集: \(\mathbf{D}^1\) (Outlook = Sunny), \(\mathbf{D}^2\) (Outlook = Overcast), \(\mathbf{D}^3\) (Outlook = Rain). 所占比例:Sunny \(=\frac{5}{14}=0.357\), Overcast \(=\frac{4}{14}=0.286\), Rain \(=\frac{5}{14} = 0.357\).
分别计算出它们的信息熵:
\(Ent(\mathbf{D}^1)= -(\frac {2}{5}\log_2\frac {2}{5}+\frac {3}{5}\log_2\frac {3}{5})=0.971\)
\(Ent(\mathbf{D}^2)= 0\)
\(Ent(\mathbf{D}^3)= -(\frac {3}{5}\log_2\frac {3}{5}+\frac {2}{5}\log_2\frac {2}{5})=0.971\)
于是我们可以算出属性“Outlook”的信息增益:
\(Gain(\mathbf{D},Outlook) = Ent(\mathbf{D}) - \sum_{v=1}^3\frac {|\mathbf{D}^v|}{|\mathbf{D}|} Ent(\mathbf{D}^v) \)
\(=0.9401- (0.357*0.971 + 0.286*0 +0.357*0.971 )\)
\(= 0.247\)
同理, 我们可以计算出其他属性的信息增益:
\(Gain(\mathbf{D},Temperature) = 0.029\) ; \(Gain(\mathbf{D},Humidity) = 0.152\);
\(Gain(\mathbf{D},Wind) = 0.048.\)
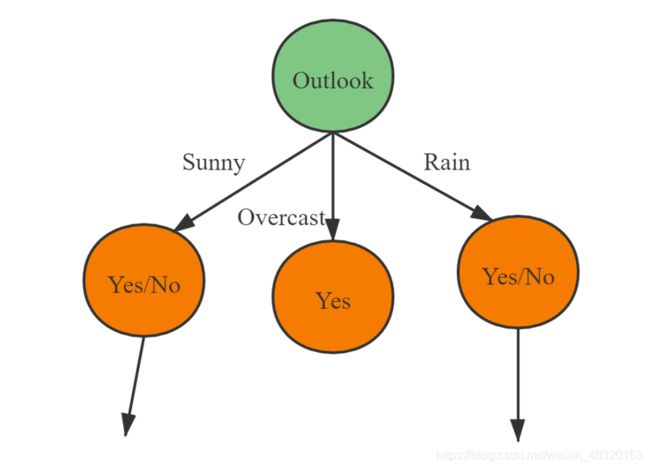
显然,“Outlook”的信息增益最大, 于是它被选为划分属性. 如下图:
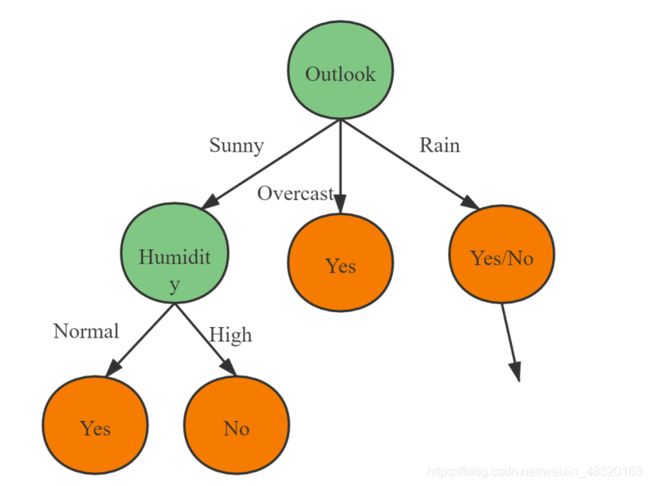
很显然还可以继续划分.以图中第一个分支结点(Outlook = Sunny)为例, 可用属性集合为{Temperature, Humidity, Wind}.
基于\(\mathbf{D}^1\)计算出各属性的信息增益:
\(Gain(\mathbf{D}^1, Temperature) = 0.571\) ; \(Gain(\mathbf{D}^1, Humidity) = 0.971\);
\(Gain(\mathbf{D}^1, Wind) = 0.020\);
所以我们选择“Humidity”作为划分属性.
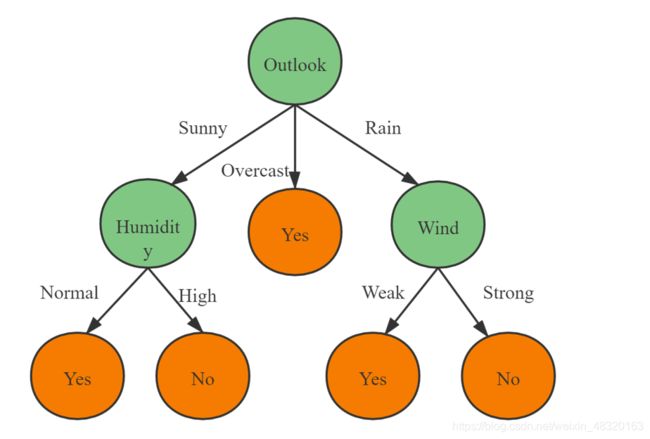
类似的, 对剩下的分支节点进行上述操作, 得到最终的决策树.
《机器学习》周志华