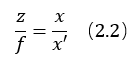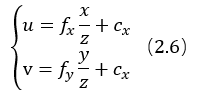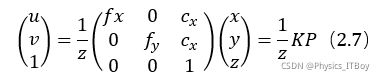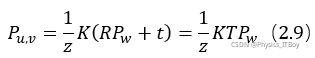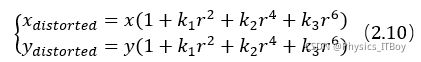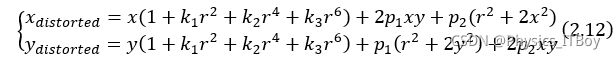【计算机视觉-从入门到精通系列】 第二章 相机模型
2.1 针孔模型
计算机视觉是一门研究如何让计算机“看”世界的学科。人要看到世界需要眼睛,计算机要看到世界同样也需要“眼睛”,计算机的“眼睛”主要就是相机。实际应用中,相机的种类纷繁复杂,包括手机和平板电脑的相机,传统的胶片相机、普通的数码相机、专业的量测相机等,还包括双目相机、RGBD相机、激光雷达等新型相机。为了精准描述相机成像过程,需要建立起对应的数学模型,这就是相机模型。相机模型是用来描述相机将三维世界中的坐标点映射到二维图像平面的过程,其中最常用也是最简单的是针孔模型,如(图2-1)所示。其中O![]() 为相机的光心,称为摄站中心,P是三维空间点,P'是成像点,f是相机焦距。针孔模型对应的物理过程是小孔成像。
为相机的光心,称为摄站中心,P是三维空间点,P'是成像点,f是相机焦距。针孔模型对应的物理过程是小孔成像。
需要说明的是,相机镜头实际使用的是凸透镜 (图2-2),但由于小孔成像和凸透镜成像具有相同的成像几何关系,因此针孔模型对凸透镜成像同样适用。
在介绍针孔模型之前,需要先简单介绍一下计算机视觉里常用的几个坐标系,它们分别是像素坐标系、相机坐标系和世界坐标系。像素坐标系是平面坐标系,原点一般为影像的左上角,也可以是左下角或影像中心,X、Y轴分为影像行、列方向。相机坐标系一般以摄站中心O为原点,X、Y![]() 轴与分别影像X、Y轴方向一致,以光轴为Z轴。世界坐标系是相机拍摄的三维场景的参考坐标系,相机位置和姿态(拍摄角度)以此作为参考。
轴与分别影像X、Y轴方向一致,以光轴为Z轴。世界坐标系是相机拍摄的三维场景的参考坐标系,相机位置和姿态(拍摄角度)以此作为参考。
针孔模型中,∆PAO与∆P'BO为相似三角形,可以得到式(2.1),式中的负号用来表示成的像是倒立的。
为了方便,可等价地将像平面放到物方同侧图(2-3),此时像点为P''。其中,∆P'BO与∆P''B'O也为相似三角形,且各边长相等,此时成像不再是倒立,式(2.1)中的负号可以去掉,得式(2.2)。
推广到三维场景可得式(2.3),其中 y是物体在相机坐标系Y轴上的坐标, y'是像素坐标系y轴上的坐标。
像素坐标系和成像平面(相机坐标系),相差一个缩放和平移。假设像点在成像平面的坐标在X轴上缩放了α倍,在Y轴上缩放了β倍,且坐标系原点平移了![]() ,则成像点P'的像素坐标
,则成像点P'的像素坐标![]() 与世界坐标的关系为(2.4)式。
与世界坐标的关系为(2.4)式。
将式(2.3)代入式(2.4)得式(2.5)
将![]() 合并成
合并成![]() ,
,![]() 合并成
合并成![]() ,得式(1.6),
,得式(1.6),![]() 、
、![]() 、
、![]() 、
、![]() 的单位是像素。
的单位是像素。
用矩阵形式来表示(2.6)式,
![]() 、
、![]() 、
、![]() 、
、![]() 组成的矩阵称为相机的内参数(Camera Intinsics)矩阵K。相机的内参与相机自身硬件相关,在相机出厂之后是固定的,有的厂家直接提供内参数,但更多的情况是需要自己确定相机内参,这就是所谓的相机标定。具体的标定方法相对比较成熟,这里不做介绍。从式(2.7)可以看出, P点坐标
组成的矩阵称为相机的内参数(Camera Intinsics)矩阵K。相机的内参与相机自身硬件相关,在相机出厂之后是固定的,有的厂家直接提供内参数,但更多的情况是需要自己确定相机内参,这就是所谓的相机标定。具体的标定方法相对比较成熟,这里不做介绍。从式(2.7)可以看出, P点坐标![]() 乘上任何非零常数,它对应的像素坐标系始终不会发生变化,这就数学上说明了单目相机无法确定物方点深度。我们假设z=1时,P点坐标为
乘上任何非零常数,它对应的像素坐标系始终不会发生变化,这就数学上说明了单目相机无法确定物方点深度。我们假设z=1时,P点坐标为![]() ,可理解为将原来的P
,可理解为将原来的P![]() 点沿着PO线移动至
点沿着PO线移动至![]() ,此时对应像素坐标也不会变化,该坐标称为归一化坐标。z=1的平面称为归一化平面。归一化坐标与归一化平面使用上会更加简洁方便。
,此时对应像素坐标也不会变化,该坐标称为归一化坐标。z=1的平面称为归一化平面。归一化坐标与归一化平面使用上会更加简洁方便。
与相机内参数相对的概念就是相机外参数。为了将每一次拍摄时的相机位姿统一在世界坐标系中,需要对各个相机坐标系进行旋转平移操作,对应的旋转矩阵R和平移向量t称为相机外参数(Camera Extinsics)。相机的外参数与相机自身硬件无关,只取决于拍摄时的位置和姿态。假设相机坐标系下P点在世界坐标系的坐标为![]() ,像素坐标系的坐标为
,像素坐标系的坐标为![]() 则
则
将式(2.7)代入式(2.8)得式(2.9)
式(2.9)隐含了将![]() 坐标由非齐次坐标到齐次坐标的转换,并用T矩阵代替R,t的旋转平移操作。
坐标由非齐次坐标到齐次坐标的转换,并用T矩阵代替R,t的旋转平移操作。
2.2 畸变模型
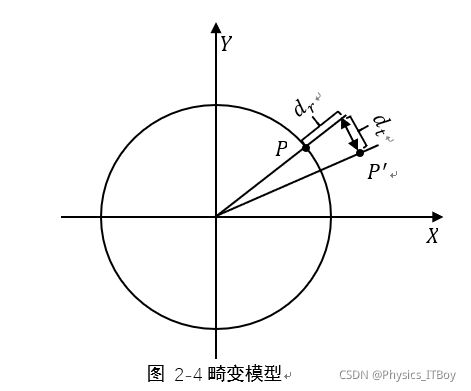
针孔模型是一个理想模型,它与实际情况存在差异,最显著的差异就是相机畸变。造成相机畸变主要有三个原因:一是透镜自身形状对光线传播的影像;二是透镜光学中心和几何中心不一致;三是镜头设计缺陷与加工安装误差。根据畸变对不同方向影响可以分为径向畸变和切向畸变(图2-4)。其中P点为理想的像点,P'为实际的像点。dr为径向畸变,dt为切向畸变。
根据造成畸变的原因来分类,可以更具体地分为径向畸变、离心畸变、薄棱镜畸变。大多相机薄棱镜畸变可以忽略,这里也不进行详细介绍。我们将重点介绍更为常用的径向畸变、离心畸变。径向畸变又可以细分为桶形畸变和枕形畸变。
为了能够数值描述径向畸变,需要两个前提,一是径向畸变是中心对称的;二是径向畸变是连续变化的。这就要求出厂的相机硬件是中心对称且表面光滑的,对于大多数的厂商而言这个并不难做到。前面提到,单目相机无法感知深度。因此,在相机坐标系中,相机畸变只影响x,y值。为了方便,在畸变模型中,我们将统一采用归一化坐标。对于相机坐标系内的P点,它的坐标是![]() ,因为存在相机畸变,通过相机看到它的坐标为
,因为存在相机畸变,通过相机看到它的坐标为![]() 。记r为P与坐标系原点的距离,因为径向畸变为中心对称,因而径向畸变与r相关。又因为径向畸变连续变化,因此可以使用一个多项式来拟合在不同的r处畸变前后的P位置的关系。可以用式(2.10)来描述。二项式系数多少可以根据具体的精度需要来决定,一般
。记r为P与坐标系原点的距离,因为径向畸变为中心对称,因而径向畸变与r相关。又因为径向畸变连续变化,因此可以使用一个多项式来拟合在不同的r处畸变前后的P位置的关系。可以用式(2.10)来描述。二项式系数多少可以根据具体的精度需要来决定,一般![]() 、
、![]() 就已经够用。
就已经够用。
离心畸变的几何分析与公式推导相对比较复杂,这里我们直接给出最后公式(2.11),有兴趣可以参考相关论文。
同时考虑径向畸变与离心畸变,于是有式(2.12)
最后根据相机内参可以得到在考虑畸变时相机坐标系与像素坐标系之间的关系,如式(2.13)
实际应用中对于相机畸变一般使用k1、k2、k3、 p1、p2这几个参数。
总结:针孔模型描述了相机的成像过程,但针孔模型是理想模型,它与实际的相机成像存在差异,为了消除这个差异需要使用畸变模型。在计算机视觉领域中,针孔模型和畸变模型适用于绝大多数的光学相机。