【2251. 花期内花的数目】
来源:力扣(LeetCode)
描述:
给你一个下标从 0 开始的二维整数数组 flowers ,其中 flowers[i] = [starti, endi] 表示第 i 朵花的 花期 从 starti 到 endi (都 包含)。同时给你一个下标从 0 开始大小为 n 的整数数组 people ,people[i] 是第 i 个人来看花的时间。
请你返回一个大小为 n 的整数数组 answer ,其中 answer[i] 是第 i 个人到达时在花期内花的 数目 。
示例 1:
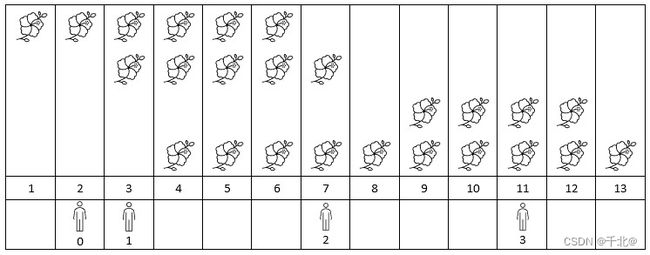
输入:flowers = [[1,6],[3,7],[9,12],[4,13]], people = [2,3,7,11]
输出:[1,2,2,2]
解释:上图展示了每朵花的花期时间,和每个人的到达时间。
对每个人,我们返回他们到达时在花期内花的数目。
示例 2:
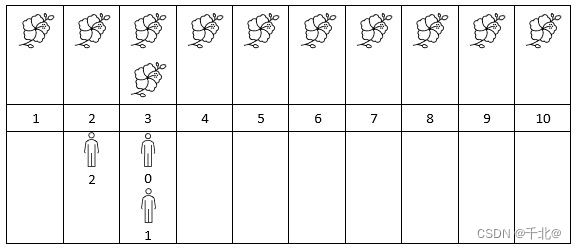
输入:flowers = [[1,10],[3,3]], people = [3,3,2]
输出:[2,2,1]
解释:上图展示了每朵花的花期时间,和每个人的到达时间。
对每个人,我们返回他们到达时在花期内花的数目。
提示:
- 1 <= flowers.length <= 5 * 104
- flowers[i].length == 2
- 1 <= starti <= endi <= 109
- 1 <= people.length <= 5 * 104
- 1 <= people[i] <= 109
方法一:差分数组 + 离线查询
思路与算法
本题可以转换为经典的「差分」思想,由于每朵花开的周期是固定的,第 iii 朵花开的周期为 [starti, endi],即区间 [starti, endi] 内每个时间点都有一朵花正处于开放状态,此时假设第 j 个人到达的时间点为 people[j],则此时我们只需要求出 people[j] 时正处于开花状态的花朵数目即可。根据差分的性质,对差分数组求前缀和即可得到当前元素的值,此时我们只需要对区间 [0,people[j]] 之间求前缀和,即可得到时间点为 people[j] 开花的数目。
具体地,由于本题中花开时间的取值范围为 0 ≤ starti ≤ endi ≤ 1090 ,这就决定了我们无法直接使用数组来计算前缀和,但可以将时间点进行离散化,利用有序集合来记录端点的变化量即可,在时间点 starti 上开花的数量增加了 1,在时间点 endi + 1 开花的数量减少了 1。遍历整个 flowers 数组,利用有序集合 cnt 统计每次花开放区间端点的变化量。此时根据差分的性质,只需对所有小于等于 people[j] 的端点变化量求和即可计算出 people[j] 时间点处于开花状态的花朵数目。由于 cnt 本身为有序集合,对其直接遍历即为有序,从小到大累加所有的变化量即可依次得到从早到晚开花的数目。 为了避免每次重复计算,可将 people 从小到大排序,这样可在遍历 people 的同时遍历 cnt。此时可以利用双指针,一个指向数组 people,另一个指针指向有序集合 cnt 即可。
代码:
class Solution {
public:
vector<int> fullBloomFlowers(vector<vector<int>>& flowers, vector<int>& persons) {
map<int, int> cnt;
for (auto &flower : flowers) {
cnt[flower[0]]++;
cnt[flower[1] + 1]--;
}
int m = persons.size();
vector<int> ves(m);
iota(ves.begin(), ves.end(), 0);
sort(ves.begin(), ves.end(), [&](int a, int b) {
return persons[a] < persons[b];
});
vector<int> ans(m);
int curr = 0;
auto it = cnt.begin();
for (int x : ves) {
while (it != cnt.end() && it->first <= persons[x]) {
curr += it->second;
it++;
}
ans[x] = curr;
}
return ans;
}
};
时间 264ms 击败 73.61%使用 C++ 的用户
内存 82.95MB 击败 45.84%使用 C++ 的用户
复杂度分析
- 时间复杂度:O(nlogn+mlogm),其中 n 表示数组 flowers 的长度,m 表示数组 people 的长度。由于 cnt 为有序集合,因此每次插入的时间为 O(logn),一共需要插入 n 个元素,因此构建有序集合的时间为 O(nlogn),people 排序花费的时间为 O(mlogm),因此总的时间为 O(nlogn+mlogm)。
- 空间复杂度: O(n+m),其中 n 表示数组 flowers 的长度,m 表示数组 people 的长度。存储 n 个元素的有序集合需要使用的空间为 O(n),由于本题目使用了离线查询,即需要保存 people 的原始索引,使用的空间为 O(m),因此总的空间为 O(n+m)。
方法二:二分查找
思路与算法
第 i 到达的时间为 people[i],假设在 people[i] 时间点之前花开的数目为 x,在 people[i] 时间之前花谢的数目为 y,则在 people[i] 时间点还处于开花状态的数目等于 x − y。我们只需要找到 start ≤ people[i] 的花朵数目,减去 end < people[i] 的花朵数目即为 people[i] 时间点可以看到花开的数目。 根据以上分析,我们可以单独统计起始时间 start 与结束 end,利用二分查找即可快速查找结果。
- 首先需要将所有的起始时间start、结束时间 end 按照从早到晚进行排序;
- 设第 i 个人到达的时间 people[i],利用二分查找找到 starti ≤ people[i] 的花朵数目为 x,利用二分查找找到 endi < people[i] 的花朵数目为 y,则第 i 个人可以看到的花朵数目为 x − y;
- 依次遍历并统计每个人的查询结果即可;
代码:
class Solution {
public:
vector<int> fullBloomFlowers(vector<vector<int>> &flowers, vector<int> &persons) {
int n = flowers.size();
vector<int> starts(n), ends(n);
for (int i = 0; i < n; ++i) {
starts[i] = flowers[i][0];
ends[i] = flowers[i][1];
}
sort(starts.begin(), starts.end());
sort(ends.begin(), ends.end());
int m = persons.size();
vector<int> ans(m);
for (int i = 0; i < m; ++i) {
int x = upper_bound(starts.begin(), starts.end(), persons[i]) - starts.begin();
int y = lower_bound(ends.begin(), ends.end(), persons[i]) - ends.begin();
ans[i] = x - y;
}
return ans;
}
};
时间 248ms 击败 87.50%使用 C++ 的用户
内存 75.33MB 击败 77.08%使用 C++ 的用户
复杂度分析
- 时间复杂度: O((n+m)×logn)O((n + m) ,其中 n 表示数组 flowers 的长度,m 表示数组 people 的长度。对 start, end 进行排序需要的时间为 O(nlogn),对每个到达的人进行二分查找时需要的时间为 O(logn),一共需要查询 m 次,查询时花费时间为 mlogn,总的时间复杂度为 (n+m) × logn(n + m)。
- 空间复杂度: O(n),其中 n 表示数组 flowers 的长度。需要单独保存每朵花开的时间点 start 与结束的时间点 end,需要的空间为 O(n),排序需要的空间为 O(logn),总的空间复杂度为 O(n+logn) = O(n)。
author:力扣官方题解