GAT学习

GAT

由于
信息处理能力的局限，人类会选择性地关注完整信息中的某一部分，同时忽略其他信息。这种机制大大提高了人类对信息的处理效率。
注意力机制的核心在于对给定信息进行权重分配，权重高的信息意味着需要系统进行重点加工。
图注意力网络（Graph Attention Networks）：自动学习图中节点对节点之间的影响度

注意力机制的定义

上式中：
Source是需要系统处理的信息源
Query代表某种条件或者先验信息
Attention Value是给定Query信息的条件下，通过注意力机制从Source中提取得到的信息。
similarity（Query，Keyi）表示Query向量和Key向量的相关度，最直接的方法是可以取两向量的内积。内积越大，相似度越高

图注意力层

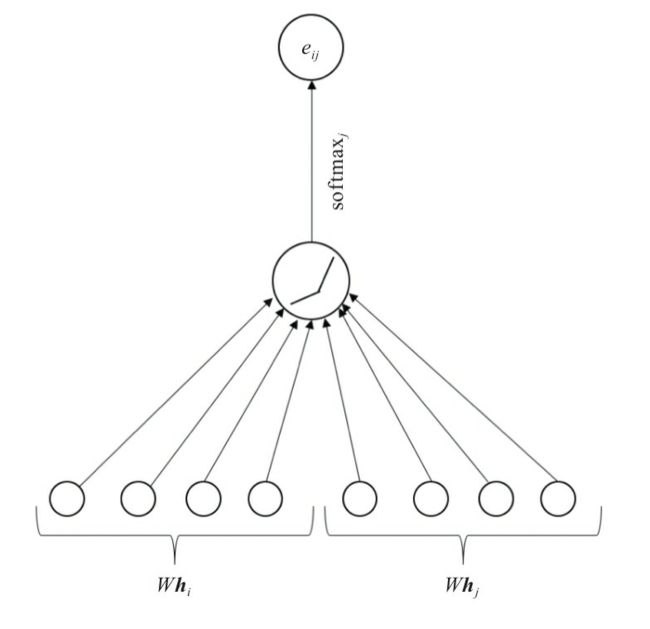
上图中，h_i：h_i∈R^d(l)任意节点v_i在第l层所对应的特征向量。
经过一个以注意力机制为核心的聚合操作之后，输出的是每个节点的新的特征向量h_i’, h_i’∈R^d(l+1)。我们将这个聚合操作称为图注意力层。

假设中心节点为v_i, 我们设邻居节点V_j到v_i的权重系数e_ij 为：

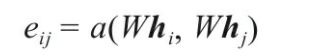
W∈R^d(l+1)xd(l) 是该层节点特征变换的权重系数。
α(·) 是计算两个节点相关度的函数。原则上可以计算图中任意一个节点到节点v_i的权重系数，为简化计算将其限制在一节邻居内（在GAT中，将自己也视为自己的邻居）。这里的α可以用向量的内积，只要保证最后输出一个实数就可以。
这里采用如下方程：

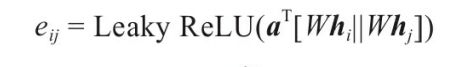
α是一个权重参数，α∈R^2d(l+1).这个R表示是实数，2d表示长度，l+1是层数。
W∈R^d(l+1)xd(l) 是该层节点特征变换的权重系数。
h_i h_j表示节点的特征向量。
α_ij表示i-j之间的attention系数。 表示i-j之间的关联程度，重要性之类的。GAT使用自注意力机制来计算节点的邻居节点对节点 i 的贡献，并以加权的方式将邻居节点的特征融合到节点 i 的特征中。
$hi$ 表示i节点的特征。
W是一个系数
[Wh_i||Wh_j] 表示将两个特征拼接在一起
$a$^T 表示一个可学习的系数。
$h$_j表示j节点（为 i 的邻居）的特征
$h$_i表示节点i的特征
$h$_i’ 表示i节点聚合了所有邻居之后的特征。
e_ij: 邻居节点v_j到v_i的权重系数
wh_i 是节点i的特征表示h_i经过权重矩阵weight_w的线性变换后得到的结果, 可以理解为“节点i的权重特征”或“节点i的特征映射”

多头注意力机制

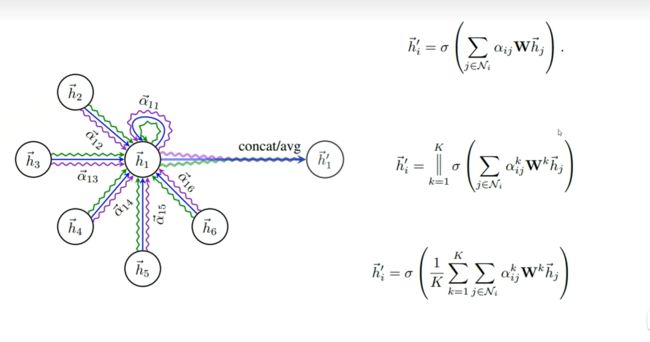
$h$_i’ 表示i节点聚合了所有邻居之后的特征。
第二行的表示选取了多个参数，（α_ij、W）得到节点的多个特征向量。||表示将这些特征向量拼接到一起。
第三行是将多个特征向量求和取平均。

---

GATConv层中forward函数步骤解析：

1. 计算wh。wh:带权特征向量

这里的wh是所有节点的带权特征向量，wh_i和wh_j都包含在其中。
x是所有节点的初始特征向量，与weight_w这样一个权重相乘后得到带权特征向量。

wh = torch.mm(x, self.weight_w)     # 公式中的[Whi||whj], 包含所有结点的特征表示，每一行对应一个节点的特征 wh:[2708,16], x:[2708,1433], weight_w:[1433, 16]

2. 计算注意力分数e

e是一个考虑了所有点，但是没有考虑邻居关系的注意力分数矩阵。e_ij表示邻居节点v_j到v_i的权重系数，也叫注意力分数。就是v_j对于v_i来说的的注意力系数是多少。这里考虑了任意两个节点的注意力系数，但是GAT中只需要考虑一阶邻居的注意力系数（自己也算自己的邻居）

e = torch.mm(wh, self.weight_a[: self.out_channels]) + torch.matmul(wh, self.weight_a[self.out_channels:]).T # 公式中的eij, 表示注意力分数

3. 激活注意力分数e

e = self.leakyrelu(e)

4. 由边的索引获取邻接矩阵

if self.adj == None:
    self.adj = to_dense_adj(edge_index).squeeze()   # 将稀疏邻接矩阵转换为密集邻接矩阵

     # 添加自环，考虑自身加权
    if self.add_self_loops:
         self.adj += torch.eye(x.shape[0]).to(device)

5. 获得注意力分数矩阵。 attention[i][j]表示i j之间的注意力分数

这里的注意力分数矩阵attention是从注意力分数e演变过来的。前面说e考虑了任意两点之间的权重系数，但是我们只要一阶邻居的，所以这里是做了这么个操作。

attention = torch.where(self.adj > 0, e, -1e9 * torch.ones_like(e))

torch.where详解：

torch.where(condition, a, b)
如果condition满足，返回a，如果不满足，返回b

6. 归一化注意力分数

因为要保证所有邻居的权重系数和为1，所以要进行归一化。

attention = F.softmax(attention, dim=1)  # attention:[2708, 2708]

7. 加权融合特征向量

前面的一系列操作就是为了得到注意力系数矩阵attention，然后要将原来的特征项向量h_i通过注意力系数进行加权：

output = torch.mm(attention, wh)        # output: [2707,2708]*[2708,16]=[2708,16]

8.添加偏置

if self.bias != None:
    return output + self.bias.squeeze().unsqueeze(0) # self.bias是[16, 1],要变成[16]或者[1, 16]才能自动broadcast相加。可以不用unsqueeze()
else:
    return output

完整代码

import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
from scipy.sparse import coo_matrix
from torch_geometric.datasets import Planetoid
from torch_geometric.utils import to_dense_adj

# 1.加载Cora数据集
dataset = Planetoid(root='./data/Cora', name='Cora')    # 从PYG中加载数据集，保存到本地根目录的/data/Cora下


# 2.定义GATConv层
class GATConv(nn.Module):
    def __init__(self, in_channels, out_channels, heads=1, add_self_loops=True, bias=True):   # GATConv1: in_channels:1433, out_channel:16
        super(GATConv, self).__init__()     # 子类的初始化，但是在调用子类的初始化时会调用父类的初始化，所以相当于调用nn.Moudle的初始化
        self.in_channels = in_channels  # 输入图节点的特征数
        self.out_channels = out_channels  # 输出图节点的特征数
        self.adj = None
        self.add_self_loops = add_self_loops

        # 定义参数 θ
        self.weight_w = nn.Parameter(torch.FloatTensor(in_channels, out_channels))  #公式中的W  [1433， 16] nn.Parameter()将张量封装为可训练参数。
        self.weight_a = nn.Parameter(torch.FloatTensor(out_channels * 2, 1))        #公式中的a^T  weight_a:[32,1] 由于要和[Whi||whj]拼接在一起，所以size要*2
        # weight_a: 将节点的特征映射成注意力分数

        if bias:
            self.bias = nn.Parameter(torch.FloatTensor(out_channels, 1))
        else:
            self.register_parameter('bias', None)                                   # 注册上一个参数

        self.leakyrelu = nn.LeakyReLU()
        self.init_parameters()

    # 初始化可学习参数
    def init_parameters(self):
        nn.init.xavier_uniform_(self.weight_w)          # 使用xavier初始化方式初始化参数
        nn.init.xavier_uniform_(self.weight_a)

        if self.bias != None:
            nn.init.zeros_(self.bias)

    def forward(self, x, edge_index):
        # 1.计算wh，进行节点空间映射 wh:带权特征向量
        wh = torch.mm(x, self.weight_w)     # 公式中的[Whi||whj], 包含所有结点的特征表示，每一行对应一个节点的特征 wh:[2708,16], x:[2708,1433], weight_w:[1433, 16]

        # 2.计算注意力分数e    e:[2708, 2708],用到了广播机制 由[2708, 1] + [1, 2708]搞起来的.
        # 第一项得到一个点对其他点的注意力分数，第二项一转置得到所有点对其他点的注意力分数，然后通过广播机制相加，得到所有点对所有点的注意力分数。
        # 但是这里只是初始化的，并未考虑节点的邻居关系。
        e = torch.mm(wh, self.weight_a[: self.out_channels]) + torch.matmul(wh, self.weight_a[self.out_channels:]).T # 公式中的eij, 表示注意力分数

        # 3.激活
        e = self.leakyrelu(e)

        # 4.由边的索引获取邻接矩阵
        if self.adj == None:
            self.adj = to_dense_adj(edge_index).squeeze()   # 将稀疏邻接矩阵转换为密集邻接矩阵

            # 添加自环，考虑自身加权
            if self.add_self_loops:
                self.adj += torch.eye(x.shape[0]).to(device)

        # 5.获得注意力分数矩阵。 attention[i][j]表示i j之间的注意力分数
        attention = torch.where(self.adj > 0, e, -1e9 * torch.ones_like(e))

        # 6.归一化注意力分数
        attention = F.softmax(attention, dim=1)  # attention:[2708, 2708]

        # 7.加权融合特征向量
        output = torch.mm(attention, wh)        # output: [2707,2708]*[2708,16]=[2708,16]

        # 8.添加偏置
        if self.bias != None:
            return output + self.bias.squeeze().unsqueeze(0) # self.bias是[16, 1],要变成[16]或者[1, 16]才能自动broadcast相加
        else:
            return output


# 3.定义GAT网络
class GAT(nn.Module):
    def __init__(self, num_node_features, num_classes): # num_node_features:1433  num_classes:7
        super(GAT, self).__init__()
        self.conv1 = GATConv(in_channels=num_node_features,
                             out_channels=32,
                             heads=2)   #heads表示多头
        self.conv2 = GATConv(in_channels=32,
                             out_channels=16,
                             heads=2)
        self.conv3 = GATConv(in_channels=16,
                             out_channels=num_classes,
                             heads=1)

    def forward(self, data):
        x, edge_index = data.x, data.edge_index

        x = self.conv1(x, edge_index)       # 将节点特征x和边的索引edge_index作为输入通道和输出通道
        x = F.relu(x)
        x = F.dropout(x, training=self.training)    # training用于区分是否是训练模式
        x = self.conv2(x, edge_index)
        x = F.relu(x)
        return F.log_softmax(x, dim=1)      # 计算节点的类别概率分布


device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')  # 设备
epochs = 200  # 学习轮数 训练轮数
lr = 0.0003  # 学习率
num_node_features = dataset.num_node_features  # 每个节点的特征数
num_classes = dataset.num_classes  # 每个节点的类别数
data = dataset[0].to(device)  # Cora的一张图

# 4.定义模型
model = GAT(num_node_features, num_classes).to(device)      # 将模型放到指定设备上运算
optimizer = torch.optim.Adam(model.parameters(), lr=lr)  # 优化器
loss_function = nn.NLLLoss()  # 损失函数

# 训练模式
model.train()

for epoch in range(epochs):

    pred = model(data)

    loss = loss_function(pred[data.train_mask], data.y[data.train_mask])  # 损失

    correct_count_train = torch.eq(pred[data.train_mask].argmax(axis=1), data.y[data.train_mask]).sum().item()  # epoch正确分类数目
    # correct_count_train = pred.argmax(axis=1)[data.train_mask].eq(data.y[data.train_mask]).sum().item()  # epoch正确分类数目
    acc_train = correct_count_train / data.train_mask.sum().item()  # epoch训练精度
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    if epoch % 20 == 0:
        print("【EPOCH: 】%s" % str(epoch + 1))
        print('训练损失为：{:.4f}'.format(loss.item()), '训练精度为：{:.4f}'.format(acc_train))

print('【Finished Training！】')

# 模型验证
model.eval()
pred = model(data)

# 训练集（使用了掩码）
# 再在测试集上看看效果
correct_count_train = pred.argmax(axis=1)[data.train_mask].eq(data.y[data.train_mask]).sum().item()
acc_train = correct_count_train / data.train_mask.sum().item()
loss_train = loss_function(pred[data.train_mask], data.y[data.train_mask]).item()

# 测试集
correct_count_test = pred.argmax(axis=1)[data.test_mask].eq(data.y[data.test_mask]).sum().item()
acc_test = correct_count_test / data.test_mask.sum().item()
loss_test = loss_function(pred[data.test_mask], data.y[data.test_mask]).item()

print('Train Accuracy: {:.4f}'.format(acc_train), 'Train Loss: {:.4f}'.format(loss_train))
print('Test  Accuracy: {:.4f}'.format(acc_test), 'Test  Loss: {:.4f}'.format(loss_test))

后记

今天，花了一天的时间学这个。对我来说，我觉得进步很大，终于不是一头雾水了，终于拨开云雾见青天了。
生活，重要是过的开心，最好的方法就是享受当下。