怒刷LeetCode的第18天(Java版)
目录
第一题
题目来源
题目内容
解决方法
方法一:置换
方法二:哈希集合
方法三:递归
第二题
题目来源
题目内容
解决方法
方法一:双指针法
方法二:动态规划
方法三:栈
方法四:两边扫描
方法五:单调栈
第三题
题目来源
题目内容
解决方法
方法一:两层循环
方法二:模拟手工乘法
方法三:BigInteger类
第一题
题目来源
41. 缺失的第一个正数 - 力扣(LeetCode)
题目内容
解决方法
方法一:置换
要找到未排序整数数组中缺失的最小正整数,可以使用一种"置换"的思路来解决。
- 首先,我们对数组进行遍历,将所有非正整数和大于数组长度的数置为一个特定的值,比如n+1。这是因为我们关心的是在1到n之间的正整数。
- 接下来,再次遍历数组,对于每个正整数x,我们将位置x-1上的数字标记为负数。标记的方式是取绝对值并且改变符号。这样做的目的是通过标记来记录该位置上的正整数是否存在。
- 最后,我们再次遍历数组,如果某个位置上的数字仍为正数,说明该位置上的正整数缺失。我们返回该位置的索引+1作为结果。
- 如果数组中所有位置上的数字都被标记成了负数,说明1到n这个范围内的所有正整数都存在,那么缺失的最小正整数就是n+1。
class Solution {
public int firstMissingPositive(int[] nums) {
int n = nums.length;
// 将所有非正整数置为n+1
for (int i = 0; i < n; i++) {
if (nums[i] <= 0) {
nums[i] = n + 1;
}
}
// 对于每个正整数x,将位置x-1上的数字置为负数
for (int i = 0; i < n; i++) {
int num = Math.abs(nums[i]);
if (num <= n) {
nums[num - 1] = -Math.abs(nums[num - 1]);
}
}
// 返回第一个位置上仍为正数的索引+1
for (int i = 0; i < n; i++) {
if (nums[i] > 0) {
return i + 1;
}
}
// 如果都为负数,则返回n+1
return n + 1;
}
}
复杂度分析:
首先,让我们逐步分析算法的复杂度:
- 第一个循环遍历数组,将非正整数置为特定值(n+1),时间复杂度为O(n)。
- 第二个循环遍历数组,将每个正整数对应位置上的数字标记为负数,时间复杂度为O(n)。
- 第三个循环遍历数组,查找第一个仍为正数的位置,时间复杂度为O(n)。
因此,整体算法的时间复杂度为O(n)。
在空间复杂度方面,我们只使用了常数级别的额外空间来存储一些临时变量,所以空间复杂度为O(1),即常数级别的额外空间。
综上所述,这个解决方案的时间复杂度是O(n),空间复杂度是O(1)。
LeetCode运行结果:
方法二:哈希集合
除了置换的思路,还可以使用哈希集合来解决这个问题。
这个解决方案首先将数组中小于等于0的数置为大于n的数(无效数),然后创建一个哈希集合,用于存储1到n范围内的正整数。接着,遍历数组,将数组中的正整数加入哈希集合。
最后,遍历1到n的每个数字,找到第一个不在哈希集合中的正整数。如果1到n都在哈希集合中,则返回n+1作为结果。
import java.util.HashSet;
class Solution {
public int firstMissingPositive(int[] nums) {
int n = nums.length;
// 将数组中小于等于0的数置为大于n的数(无效数)
for (int i = 0; i < n; i++) {
if (nums[i] <= 0) {
nums[i] = n + 1;
}
}
// 创建一个哈希集合,用于存储正整数
HashSet set = new HashSet<>();
// 将数组中的正整数加入哈希集合
for (int i = 0; i < n; i++) {
if (nums[i] <= n) {
set.add(nums[i]);
}
}
// 遍历1到n,找到第一个不在哈希集合中的正整数
for (int i = 1; i <= n; i++) {
if (!set.contains(i)) {
return i;
}
}
// 如果1到n都在哈希集合中,则返回n+1
return n + 1;
}
}
复杂度分析:
我们来分析一下这个解决方案的复杂度:
- 第一个循环遍历数组,将非正整数置为特定值,时间复杂度为O(n)。空间复杂度为O(1),因为只使用了常数级别的额外空间。
- 创建哈希集合并将正整数加入其中,需要遍历数组,时间复杂度为O(n)。空间复杂度为O(n),因为需要使用额外的哈希集合来存储正整数。
- 第三个循环遍历1到n的每个数字,查找第一个不在哈希集合中的正整数,时间复杂度为O(n)。
因此,整体算法的时间复杂度为O(n),空间复杂度为O(n)。
与置换的方法相比,使用哈希集合的方法在时间复杂度和空间复杂度上都是一样的,但它使用了额外的哈希集合来存储正整数。
LeetCode运行结果:
方法三:递归
除了置换和哈希集合的思路,还可以使用递归的方式来解决这个问题。
这个方法的思路是遍历数组,对于每个正数nums[i],将其放在正确的位置上,即nums[i]-1。使用递归进行交换操作,直到不能交换为止。然后再遍历数组,找到第一个不在正确位置上的数,即为缺失的最小正整数。
class Solution {
public int firstMissingPositive(int[] nums) {
int n = nums.length;
// 首先处理边界情况,如果数组为空,则结果为1
if (n == 0) {
return 1;
}
// 对于每个正数nums[i],将其放在正确的位置上,即nums[i]-1
// 这里使用递归进行交换操作,直到不能交换为止
for (int i = 0; i < n; i++) {
while (nums[i] > 0 && nums[i] <= n && nums[nums[i] - 1] != nums[i]) {
swap(nums, i, nums[i] - 1);
}
}
// 寻找第一个不在正确位置上的数,即为缺失的最小正整数
for (int i = 0; i < n; i++) {
if (nums[i] != i + 1) {
return i + 1;
}
}
// 如果所有数字都在正确位置上,则返回n+1
return n + 1;
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
复杂度分析:
- 时间复杂度:在递归方法中,我们使用递归进行交换操作,直到不能交换为止。对于每个正数nums[i],最多需要交换n次才能找到它正确的位置。因此,整个遍历过程的时间复杂度为O(n),其中n是数组的长度。
- 空间复杂度:递归方法本身并没有使用额外的空间,只是通过交换操作修改了原始数组。因此,递归方法的空间复杂度为O(1),即只使用了常数级别的额外空间。
需要注意的是,递归方法可能会导致栈溢出的问题,因为每次递归调用都会将一部分函数调用信息存储在栈中。
LeetCode运行结果:
第二题
题目来源
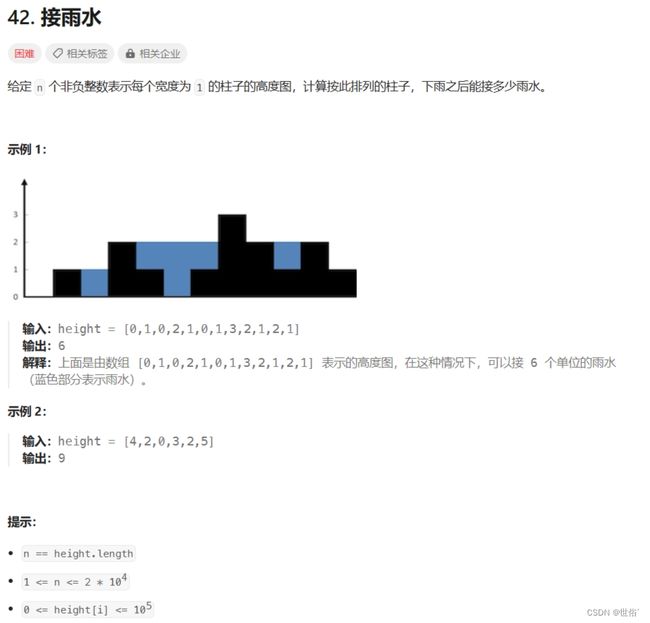
42. 接雨水 - 力扣(LeetCode)
题目内容
解决方法
方法一:双指针法
该解法使用双指针法,从数组的两端开始遍历。维护左右两侧的最大高度(初始值为0),然后根据左右两侧的最大高度和当前柱子的高度,计算能接到的雨水量并累加。具体操作如下:
1、使用双指针 left 和 right 分别指向数组的头部和尾部。
2、初始化左侧最大高度 leftMax 和右侧最大高度 rightMax,初始值都为0。
3、当 left < right 时,进行循环:
- 如果 height[left] < height[right],表示左侧的柱子较矮。若当前高度大于等于左侧最大高度 leftMax,则更新 leftMax,否则计算当前柱子能接到的雨水量(即 leftMax - height[left])并累加到结果中。
- 如果 height[left] >= height[right],表示右侧的柱子较矮。若当前高度大于等于右侧最大高度 rightMax,则更新 rightMax,否则计算当前柱子能接到的雨水量(即 rightMax - height[right])并累加到结果中。
- 更新指针:向内移动高度较低的那个指针(即左侧指针 left 向右移动或右侧指针 right 向左移动)。
4、最后,返回累加得到的雨水量作为结果。
class Solution {
public int trap(int[] height) {
int n = height.length;
if (n == 0) {
return 0;
}
int left = 0, right = n - 1;
int leftMax = 0, rightMax = 0;
int ans = 0;
while (left < right) {
// 如果左边的高度小于右边的高度
if (height[left] < height[right]) {
// 更新左侧最大高度
if (height[left] >= leftMax) {
leftMax = height[left];
} else {
// 累加雨水量
ans += leftMax - height[left];
}
left++;
}
// 如果左边的高度大于等于右边的高度
else {
// 更新右侧最大高度
if (height[right] >= rightMax) {
rightMax = height[right];
} else {
// 累加雨水量
ans += rightMax - height[right];
}
right--;
}
}
return ans;
}
}
复杂度分析:
- 时间复杂度:该算法只需要遍历一遍数组,因此时间复杂度是 O(n),其中 n 是数组的长度。
- 空间复杂度:该算法只需要常数级别的额外空间,因此空间复杂度是 O(1)。
LeetCode运行结果:
方法二:动态规划
除了双指针法之外,还可以使用动态规划来解决这个问题。
该解法使用两个数组 leftMax 和 rightMax 分别存储每个位置左侧和右侧的最大高度。具体操作如下:
- 创建两个长度为
n的数组leftMax和rightMax。 - 初始化
leftMax[0] = height[0]和rightMax[n-1] = height[n-1],即第一个位置和最后一个位置的最大高度分别是自身的高度。 - 计算每个位置左侧的最大高度:
- 从位置 1 开始遍历到位置
n-1。 - 对于每个位置
i,leftMax[i]是leftMax[i-1]和height[i]中的较大值。
- 从位置 1 开始遍历到位置
- 计算每个位置右侧的最大高度:
- 从位置
n-2开始倒序遍历到位置 0。 - 对于每个位置
i,rightMax[i]是rightMax[i+1]和height[i]中的较大值。
- 从位置
- 初始化结果变量
ans = 0。 - 遍历每个位置,计算每个位置能接到的雨水量:
- 对于每个位置
i,能接到的雨水量是Math.min(leftMax[i], rightMax[i]) - height[i]。 - 将计算得到的雨水量累加到结果变量
ans中。
- 对于每个位置
- 返回结果变量
ans作为答案。
class Solution {
public int trap(int[] height) {
int n = height.length;
if (n == 0) {
return 0;
}
int[] leftMax = new int[n]; // 存储每个位置左侧的最大高度
int[] rightMax = new int[n]; // 存储每个位置右侧的最大高度
leftMax[0] = height[0];
rightMax[n-1] = height[n-1];
// 计算每个位置左侧的最大高度
for (int i = 1; i < n; i++) {
leftMax[i] = Math.max(leftMax[i-1], height[i]);
}
// 计算每个位置右侧的最大高度
for (int i = n - 2; i >= 0; i--) {
rightMax[i] = Math.max(rightMax[i+1], height[i]);
}
int ans = 0;
// 计算每个位置能接到的雨水量
for (int i = 0; i < n; i++) {
ans += Math.min(leftMax[i], rightMax[i]) - height[i];
}
return ans;
}
}
复杂度分析:
- 时间复杂度:该算法需要进行三次遍历,分别是计算每个位置左侧的最大高度、计算每个位置右侧的最大高度以及计算每个位置能接到的雨水量。每次遍历都需要遍历整个数组,因此时间复杂度是 O(n),其中 n 是数组的长度。
- 空间复杂度:该算法使用了两个额外的数组 leftMax 和 rightMax,它们的长度都是 n,因此空间复杂度是 O(n)。除此之外,还需要使用常数级别的额外空间来存储一些临时变量,因此总体的空间复杂度也是 O(n)。
LeetCode运行结果:
方法三:栈
除了双指针法和动态规划,还可以使用栈来解决这个问题。
该解法使用栈来存储数组的索引,栈中的元素按照递减的方式存储。具体操作如下:
- 初始化结果变量
ans = 0和一个空栈stack,用于存储数组的索引。 - 遍历每个位置
i,对于每个位置:- 如果栈不为空且当前位置的高度大于栈顶位置的高度,则说明可以形成一个凹槽。
- 循环弹出栈顶位置
top,直到栈为空或者当前位置的高度小于等于栈顶位置的高度。 - 如果栈为空,表示无法形成凹槽,结束循环。
- 计算当前位置和新栈顶位置之间的距离
distance。 - 计算凹槽的高度
boundedHeight,即当前位置和新栈顶位置的高度的最小值减去弹出的栈顶位置的高度。 - 更新结果变量,累加凹槽的面积,即
ans += distance * boundedHeight。 - 将当前位置入栈。
- 返回结果变量
ans作为答案。
class Solution {
public int trap(int[] height) {
int n = height.length;
if (n == 0) {
return 0;
}
int ans = 0; // 存储结果
Stack stack = new Stack<>(); // 存储数组索引
// 遍历每个位置
for (int i = 0; i < n; i++) {
// 如果当前位置的高度大于栈顶位置的高度,则可以形成凹槽
while (!stack.isEmpty() && height[i] > height[stack.peek()]) {
int top = stack.pop(); // 弹出栈顶位置
if (stack.isEmpty()) {
break; // 栈为空,无法形成凹槽
}
int distance = i - stack.peek() - 1; // 计算距离
int boundedHeight = Math.min(height[i], height[stack.peek()]) - height[top]; // 计算高度
ans += distance * boundedHeight; // 更新结果
}
stack.push(i); // 将当前位置入栈
}
return ans;
}
}
复杂度分析:
- 时间复杂度:该算法只需要对数组进行一次遍历,每个位置的入栈和出栈操作都是常数时间复杂度。因此,时间复杂度为 O(n),其中 n 是数组的长度。
- 空间复杂度:该算法使用了一个栈来存储索引,最坏情况下栈的大小会达到数组的长度,因此空间复杂度为 O(n)。除此之外,还需要使用常数级别的额外空间来存储一些临时变量,因此总体的空间复杂度也是 O(n)。
LeetCode运行结果:
方法四:两边扫描
除了双指针法、动态规划和使用栈,还可以采用两边扫描的方法来解决这个问题。
该解法使用两个指针 left 和 right 分别指向数组的左右边界,以及两个变量 leftMax 和 rightMax 分别保存左侧和右侧的最大高度。
具体操作如下:
- 初始化结果变量
ans = 0。 - 使用两个指针
left和right分别指向数组的左右边界。 - 使用两个变量
leftMax和rightMax初始化为 0,分别表示左侧和右侧的最大高度。 - 当
left小于right时,进行循环:- 如果
height[left] < height[right],说明左侧的高度较小,可以计算左侧位置能够接到的雨水量。- 如果当前位置的高度大于
leftMax,则更新leftMax。 - 否则,计算接到的雨水量并累加到结果变量
ans中。 - 将
left向右移动一位。
- 如果当前位置的高度大于
- 否则,说明右侧的高度较小,可以计算右侧位置能够接到的雨水量。
- 如果当前位置的高度大于
rightMax,则更新rightMax。 - 否则,计算接到的雨水量并累加到结果变量
ans中。 - 将
right向左移动一位。
- 如果当前位置的高度大于
- 如果
- 循环结束后,返回结果变量
ans作为答案。
class Solution {
public int trap(int[] height) {
int n = height.length;
if (n == 0) {
return 0;
}
int ans = 0;
int left = 0; // 左边界
int right = n - 1; // 右边界
int leftMax = 0; // 左侧最大高度
int rightMax = 0; // 右侧最大高度
while (left < right) {
if (height[left] < height[right]) {
// 计算左侧位置能够接到的雨水量
if (height[left] > leftMax) {
leftMax = height[left];
} else {
ans += leftMax - height[left];
}
left++;
} else {
// 计算右侧位置能够接到的雨水量
if (height[right] > rightMax) {
rightMax = height[right];
} else {
ans += rightMax - height[right];
}
right--;
}
}
return ans;
}
}
复杂度分析:
- 时间复杂度:算法需要进行一次遍历来计算能够接到的雨水量,因此时间复杂度为 O(n),其中 n 是数组的长度。
- 空间复杂度:算法只使用了常数级别的额外空间来存储变量,因此空间复杂度为 O(1)。不会随着输入规模的增加而增长。
LeetCode运行结果:
方法五:单调栈
除了上述四种常见的解法,还有一种基于单调栈的解法。
具体思路如下:
- 使用一个栈来保存数组的下标,栈中的元素满足单调递减的顺序,即栈底的元素是最大的。
- 对于数组中的每个位置,进行如下操作:
- 如果栈为空或者当前位置的高度小于等于栈顶位置的高度,将当前位置的下标入栈。
- 否则,说明当前位置的高度高于栈顶位置的高度,可以计算栈顶位置能够接到的雨水量。
- 弹出栈顶元素,并将其作为当前位置的左侧边界。
- 如果栈非空,则当前位置的右侧边界是栈顶元素;否则,右侧边界不存在。
- 计算栈顶元素和当前位置之间的雨水量,并累加到结果变量中。
- 重复步骤 2,直到当前位置的高度小于等于栈顶位置的高度。
- 循环结束后,返回结果变量即可。
class Solution {
public int trap(int[] height) {
int n = height.length;
if (n == 0) {
return 0;
}
int ans = 0;
Stack stack = new Stack<>();
for (int i = 0; i < n; i++) {
while (!stack.isEmpty() && height[i] > height[stack.peek()]) {
int top = stack.pop();
if (!stack.isEmpty()) {
int left = stack.peek();
int width = i - left - 1;
int heightDiff = Math.min(height[left], height[i]) - height[top];
ans += width * heightDiff;
}
}
stack.push(i);
}
return ans;
}
}
其中 stack 是一个栈,用于保存数组中的下标。变量 ans 初始值为 0,用于累计能够接到的雨水量。
对于数组中的每个位置,如果栈为空或者当前位置的高度小于等于栈顶位置的高度,则将当前位置的下标入栈;否则,说明当前位置的高度高于栈顶位置的高度,可以计算栈顶位置能够接到的雨水量:
- 弹出栈顶元素,并将其作为当前位置的左侧边界。
- 如果栈非空,则当前位置的右侧边界是栈顶元素;否则,右侧边界不存在。
- 计算栈顶元素和当前位置之间的雨水量,并累加到结果变量中。
- 重复上述步骤,直到当前位置的高度小于等于栈顶位置的高度。
循环结束后,返回结果变量即可。
复杂度分析:
- 时间复杂度:算法需要对数组进行一次遍历,每个元素最多入栈和出栈一次,因此时间复杂度为 O(n),其中 n 是数组的长度。
- 空间复杂度:算法使用了一个栈来保存数组的下标,栈的最大长度不超过数组的长度,因此空间复杂度为 O(n)。
总结:基于单调栈的解法在时间复杂度和空间复杂度上都是 O(n)。
LeetCode运行结果:
第三题
题目来源
43. 字符串相乘 - 力扣(LeetCode)
题目内容
解决方法
方法一:两层循环
该问题的解决方案如下:
- 定义一个长度为 m + n 的数组 res,用于保存乘积的结果,其中 m 和 n 分别是 num1 和 num2 的长度。
- 从右往左遍历 num1 的每一位,用变量 x 表示当前位的数值。
- 再从右往左遍历 num2 的每一位,用变量 y 表示当前位的数值。
- 将 x 和 y 相乘的结果加到 res 数组的对应位置上,并考虑进位。
- 最后,遍历 res 数组进行进位操作,将每一位超过10的部分进位到高位。
- 根据进位后的 res 数组构建最终的字符串结果。
- 需要注意的是,在最终的字符串结果中,要排除前导零。
class Solution {
public String multiply(String num1, String num2) {
int m = num1.length();
int n = num2.length();
int[] res = new int[m + n];
for (int i = m - 1; i >= 0; i--) {
int x = num1.charAt(i) - '0';
for (int j = n - 1; j >= 0; j--) {
int y = num2.charAt(j) - '0';
res[i + j + 1] += x * y;
}
}
for (int i = m + n - 1; i > 0; i--) {
res[i - 1] += res[i] / 10;
res[i] %= 10;
}
StringBuilder sb = new StringBuilder();
int index = 0;
while (index < m + n && res[index] == 0) {
index++;
}
while (index < m + n) {
sb.append(res[index]);
index++;
}
return sb.length() == 0 ? "0" : sb.toString();
}
}
复杂度分析:
时间复杂度分析:
在该算法中,我们使用了两重循环来计算乘法以及进行进位操作。其中,外层循环遍历了 num1 的每一位,内层循环遍历了 num2 的每一位。
假设 num1 的长度为 m,num2 的长度为 n。
- 外层循环的时间复杂度为 O(m)。
- 内层循环的时间复杂度为 O(n)。
因此,整个算法的时间复杂度为 O(m * n)。
空间复杂度分析:
在该算法中,我们使用了一个额外的数组 res 来保存乘法的结果,其长度为 m + n。
因此,整个算法的空间复杂度为 O(m + n)。
需要注意的是,最终的字符串结果需要消除前导零,但是在最坏的情况下,结果字符串的长度可能达到 m + n。因此,在构建最终结果字符串时,可能需要额外的 O(m + n) 的空间。
综上所述,该算法的时间复杂度为 O(m * n),空间复杂度为 O(m + n)。
LeetCode运行结果:
方法二:模拟手工乘法
除了使用两层循环之外,还可以通过模拟手工乘法的方式实现。
具体步骤如下:
- 首先判断两个数中是否有一个为零,如果有,则直接返回结果 "0"。
- 初始化结果数组 res,长度为 m + n,其中 m 和 n 分别是 num1 和 num2 的长度。
- 从右往左遍历 num1 的每一位数字,用变量 x 表示当前位的数值。
- 再从右往左遍历 num2 的每一位数字,用变量 y 表示当前位的数值。
- 将 x 和 y 相乘的结果加到 res 数组的对应位置上,即 res[i + j + 1] += x * y。
- 在第二次遍历 res 数组时,从右往左进行进位操作,将每一位超过10的部分进位到高位,即 res[i - 1] += res[i] / 10,并将当前位取模,即 res[i] %= 10。
- 根据进位后的 res 数组构建最终的字符串结果。
- 需要注意的是,在最终的字符串结果中,要排除前导零。
这种方法相较于两层循环的方法,少了一层循环,但是仍然需要进行进位操作。
class Solution {
public String multiply(String num1, String num2) {
if (num1.equals("0") || num2.equals("0")) {
return "0";
}
int m = num1.length();
int n = num2.length();
int[] res = new int[m + n];
for (int i = m - 1; i >= 0; i--) {
int x = num1.charAt(i) - '0';
for (int j = n - 1; j >= 0; j--) {
int y = num2.charAt(j) - '0';
res[i + j + 1] += x * y;
}
}
for (int i = m + n - 1; i > 0; i--) {
res[i - 1] += res[i] / 10;
res[i] %= 10;
}
StringBuilder sb = new StringBuilder();
int index = res[0] == 0 ? 1 : 0;
while (index < m + n) {
sb.append(res[index]);
index++;
}
return sb.toString();
}
}
复杂度分析:
时间复杂度分析:
- 遍历 num1 的每一位数字的过程需要进行 m 次循环。
- 对于每一次 num1 的遍历,又需要遍历 num2 的每一位数字,共进行了 n 次循环。
- 在每次循环中,进行了常数次的乘法操作和加法操作,所以每次循环的时间复杂度为 O(1)。
- 因此,总体上,该算法的时间复杂度为 O(m * n)。
空间复杂度分析:
- 初始化了一个结果数组 res,长度为 m + n,需要额外的空间存储计算结果,所以空间复杂度为 O(m + n)。
- 同时,还使用了若干个变量用于存储中间结果,这些变量是常数级别的,不随输入规模的增大而增大,可以忽略不计。
- 因此,总体上,该算法的空间复杂度为 O(m + n)。
需要注意的是,以上复杂度分析是基于输入字符串的长度进行的。在实际应用中,该算法的性能通常是可以接受的,因为字符串长度一般不会非常大。但如果字符串的长度非常巨大,可能会导致算法的运行时间较长。
LeetCode运行结果:
方法三:BigInteger类
除了两层循环,模拟手工乘法的方法外,还可以使用Java的BigInteger类来实现字符串相乘。
BigInteger类是Java中用于处理任意精度整数的类,可以支持很大范围的整数运算。使用BigInteger类,可以简化字符串相乘的过程。
import java.math.BigInteger;
class Solution {
public String multiply(String num1, String num2) {
BigInteger n1 = new BigInteger(num1);
BigInteger n2 = new BigInteger(num2);
BigInteger result = n1.multiply(n2);
return result.toString();
}
}以上代码直接使用BigInteger类创建两个BigInteger对象n1和n2,分别对应num1和num2。然后使用multiply方法计算它们的乘积,最后将结果转换为字符串格式返回。
需要注意的是,这种方法利用了BigInteger类的内置函数,因此不符合题目要求"不能使用任何内置的 BigInteger 库或直接将输入转换为整数",但是效率上会更高。
复杂度分析:
假设num1的长度为n1,num2的长度为n2。
- 时间复杂度:创建BigInteger对象的时间复杂度为O(max(n1, n2)),相乘操作的时间复杂度为O(n1 + n2),因此整体的时间复杂度为O(max(n1, n2))。
- 空间复杂度:创建了两个BigInteger对象和一个结果对象,因此空间复杂度为O(1)。
LeetCode运行结果: