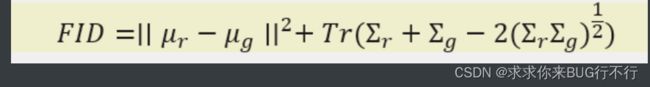【图像评价指标以及代码】 PSNR, SSIM, FID,NMSE讲解以及代码

评价指标以及计算

峰值信噪比 （PSNR）:

“Peak Signal-to-Noise Ratio”，中文意思即为峰值信噪比，是衡量图像质量的指标之一。用于衡量重构图像与原始图像之间的相似性和失真程度。PSNR只能提供关于图像整体质量的信息，不能捕捉到细节和感知的差异。

根据公式可见：当MSE越小的时候质量越好，则PSNR越大越好。


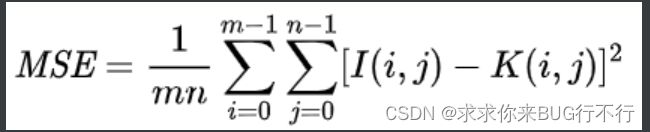
由均方误差得到，MAX1是像素里面最大的值，一般为1或者255。

def psnr(res,gt):
    mse = np.mean((res - gt) ** 2)
    if(mse == 0):
        return 100
    max_pixel = 1
    psnr = 20 * log10(max_pixel / sqrt(mse))
    return psnr

结构相似性 （SSIM）：

此方法也称为（Structural Similarity），是一种用来衡量两幅图像相似度的指标。 SSIM 方法是通过将图像看作多个区域，并比较这些区域内的结构、亮度和对比度等统 计量来进行评估的。SSIM 算法考虑了人类对图像感知的特性，更符合人眼视觉特性。 SSIM 算法比较复杂，需要对图像局部结构信息和全局结构信息进行比对。给定两个图 像 x 和 y，两张图像的结构相似性的公式可以表达为公式 2-7。

$$"SSIM"(x,y)=(2{\mu }_x{\mu }_y+c_1)(2{\sigma }_{x}y+c_2)/({\mu }_x^2+{\mu }_y^2+c_1)({\sigma }_x^2+{\sigma }_y^2+c_2)$$

返回的值是： [0, 1] 范围内的 SSIM 分数，越接近 1 表示两幅图像越相似。

from skimage.metrics import structural_similarity as ssim

def calculate_ssim(img1, img2):
    # 计算 SSIM
    ssim_score = ssim(img1, img2, multichannel=True)
    
    return ssim_score

# 示例用法
img1 = ...  # 第一幅图像数据，类型为numpy数组，范围为0-1
img2 = ...  # 第二幅图像数据，类型为numpy数组，范围为0-1

score = calculate_ssim(img1, img2)
print("SSIM score:", score)

# 或者使用下面代码也可以
#-*- codeing = utf-8 -*-
#@Time ： 2023/4/27 0027 14:43
#@Author : Tom
#@File : SSIM.py
#@Software : PyCharm

import torch
import torch.nn.functional as F

def ssim(img1, img2, window_size=11, size_average=True, full=False):
    # 常量，用于计算均值和方差
    C1 = (0.01 * 255) ** 2
    C2 = (0.03 * 255) ** 2

    # 平均池化滤波器
    window = torch.ones(3, 1, window_size, window_size).float().cuda()
    mu1 = F.conv2d(img1, window, padding=window_size//2, groups=3)
    mu2 = F.conv2d(img2, window, padding=window_size//2, groups=3)

    # 平均值和方差
    mu1_sq, mu2_sq, mu1_mu2 = mu1 ** 2, mu2 ** 2, mu1 * mu2
    sigma1_sq = F.conv2d(img1 ** 2, window, padding=window_size//2, groups=3) - mu1_sq
    sigma2_sq = F.conv2d(img2 ** 2, window, padding=window_size//2, groups=3) - mu2_sq
    sigma12 = F.conv2d(img1 * img2, window, padding=window_size//2, groups=3) - mu1_mu2

    # SSIM 的计算公式
    ssim_map = ((2 * mu1_mu2 + C1) * (2 * sigma12 + C2)) / ((mu1_sq + mu2_sq + C1) * (sigma1_sq + sigma2_sq + C2))
    if size_average:
        ssim_value = torch.mean(ssim_map)
    else:
        ssim_value = torch.mean(ssim_map, dim=(1, 2, 3))

    # 如果设置了 full=True，返回 SSIM 的值和 SSIM 图像的各通道值
    if full:
        return ssim_value, ssim_map
    else:
        return ssim_value


img1 = torch.ones(1, 3, 256, 256).cuda()
img2 = torch.ones(1, 3, 256, 256).cuda()

ssim_value = ssim(img1, img2, window_size=11)
print(ssim_value)

归一化均方误差（NMSE）：

归一化均方误差（Normalized Mean Squared Error）

NMSE的值总是在0和1之间（包括0和1），值越小表示模型的性能越好。

def nmse(res,gt):
    Norm = np.linalg.norm((gt * gt),ord=2) # 计算 'gt' 的平方的2-范数（也就是欧几里得长度），存储在变量 'Norm' 中。这一步是为了避免在分母中出现零，从而导致除零错误
    if np.all(Norm == 0): # 如果 'Norm' 等于零（也就是说，如果 'gt' 是全零向量），那么函数直接返回0。这是因为对于全零向量，任何误差都会得到无穷大的NMSE。
        return 0 
    else:
        nmse = np.linalg.norm(((res - gt) * (res - gt)),ord=2) / Norm # 算 'res' 和 'gt' 的差的平方的2-范数，然后除以 'Norm'。这就是NMSE的定义：误差的平方和除以目标值的平方和。
    return nmse

弗雷歇距离（FID）

Fréchet Inception Distance(FID) 是用于衡量生成模型生成图像与真实图像之间差异的指标，是通过比较它们在Inception v3[32]模型的特征空间中的分布距离来计算的。FID使用的特征向量是Inception v3模型的倒数第二个全连接层输出的高维向量，这个向量可以捕捉到图像的视觉特征信息。FID值可以用来度量生成模型生成的图像与真实图像的相似程度，FID值越小表示两图像在特征空间中分布越接近，相似度越高。当两幅图像完全相同时，它们的FID值为0。

$$FID=\mid \mid {\mu }_r-{\mu }_g\mid {\mid }^2+Tr({\Sigma }_r+{\Sigma }_g-2〖({\Sigma }_r{\Sigma }_g){〗}^{(}1/2))$$
公式中， 为真实图片的特征均值， 为生成图片的特征均值， 为真实图片的协方差矩阵， 为生成图片的协方差矩阵， 为迹。

import torch
import torchvision
import torchvision.transforms as transforms
from pytorch_fid import fid_score

# 准备真实数据分布和生成模型的图像数据
real_images_folder = '/path/to/real/images/folder'
generated_images_folder = '/path/to/generated/images/folder'

# 加载预训练的Inception-v3模型
inception_model = torchvision.models.inception_v3(pretrained=True)

# 定义图像变换
transform = transforms.Compose([
    transforms.Resize(299),
    transforms.CenterCrop(299),
    transforms.ToTensor(),
    transforms.Normalize(mean=[0.5, 0.5, 0.5], std=[0.5, 0.5, 0.5])
])

# 计算FID距离值
fid_value = fid_score.calculate_fid_given_paths([real_images_folder, generated_images_folder],
                                                 inception_model,
                                                 transform=transform)
print('FID value:', fid_value)

pytorch_fid版本不同，使用方式不同，需要注意一下。
两个文件夹里面图片数量需要一样，大小尽量也一样，名字最好对应，这样才会将对应图片进行计算。

最后的使用

    PSNR = []
    NMSE = []
    SSIM = []

    for i, (img, gt) in enumerate(data_loader):
        batch_size = img.size()[0]
        img = img.to(device, dtype=torch.float)
        gt = gt.to(device, dtype=torch.float)

        with torch.no_grad():
            pred = model(img)

        for j in range(batch_size):
            a = pred[j]
            # save_image([pred[j]], images_save + str(i * batch_size + j + 1) + '.png', normalize=False)
            print(images_save + str(i * batch_size + j + 1) + '.png')

        pred, gt = pred.cpu().detach().numpy().squeeze(), gt.cpu().detach().numpy().squeeze()

        for j in range(batch_size):
            PSNR.append(psnr(pred[j], gt[j]))
            NMSE.append(nmse(pred[j], gt[j]))
            SSIM.append(ssim(pred[j], gt[j]))

    PSNR = np.asarray(PSNR)
    NMSE = np.asarray(NMSE)
    SSIM = np.asarray(SSIM)

    PSNR = PSNR.reshape(-1, slice_num)
    NMSE = NMSE.reshape(-1, slice_num)
    SSIM = SSIM.reshape(-1, slice_num)

    PSNR = np.mean(PSNR, axis=1)
    NMSE = np.mean(NMSE, axis=1)
    SSIM = np.mean(SSIM, axis=1) 

    print("PSNR mean:", np.mean(PSNR), "PSNR std:", np.std(PSNR))
    print("NMSE mean:", np.mean(NMSE), "NMSE std:", np.std(NMSE))
    print("SSIM mean:", np.mean(SSIM), "SSIM std:", np.std(SSIM))

通过对每个切片进行求平均，可以得到更详细的评估结果，并且能够观察不同切片之间的差异。如果直接对整个数据进行求平均，可能无法获取到切片级别的信息。因此，进行切片并分别计算每个切片上的指标平均值是一种常见的做法。