数据结构-栈和队列-总结(缺优先级队列)
一、基础概念
1.1 C++中stack 是容器么?我们使用的stack是属于哪个版本的STL?stack 提供迭代器来遍历stack空间么?
首先大家要知道 栈和队列是STL(C++标准库)里面的两个数据结构。
C++标准库是有多个版本的,要知道我们使用的STL是哪个版本,才能知道对应的栈和队列的实现原理。
那么来介绍一下,三个最为普遍的STL版本:
- HP STL 其他版本的C++ STL,一般是以HP STL为蓝本实现出来的,HP STL是C++ STL的第一个实现版本,而且开放源代码。
- P.J.Plauger STL 由P.J.Plauger参照HP STL实现出来的,被Visual C++编译器所采用,不是开源的。
- SGI STL 由Silicon Graphics Computer Systems公司参照HP STL实现,被Linux的C++编译器GCC所采用,SGI STL是开源软件,源码可读性甚高。
接下来介绍的栈和队列也是SGI STL里面的数据结构, 知道了使用版本,才知道对应的底层实现。
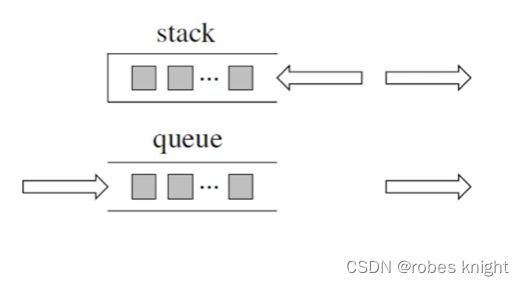
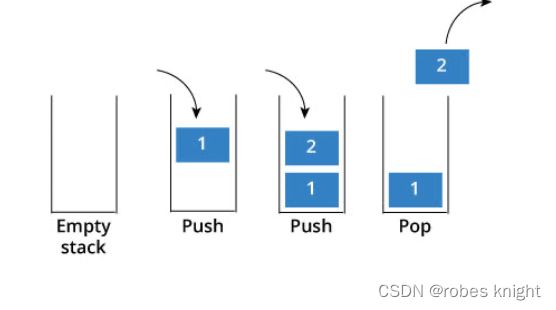
来说一说栈,栈先进后出,如图所示:
栈提供push 和 pop 等等接口,所有元素必须符合先进后出规则,所以栈不提供走访功能,也不提供迭代器(iterator)。 不像是set 或者map 提供迭代器iterator来遍历所有元素。
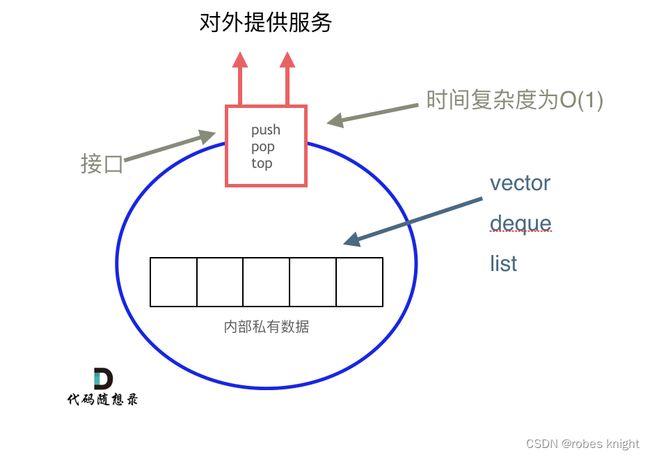
栈是以底层容器完成其所有的工作,对外提供统一的接口,底层容器是可插拔的(也就是说我们可以控制使用哪种容器来实现栈的功能)。
所以STL中栈往往不被归类为容器,而被归类为container adapter(容器适配器)。
1.2 我们使用的STL中stack是如何实现的?
从下图中可以看出,栈的内部结构,栈的底层实现可以是vector,deque,list 都是可以的, 主要就是数组和链表的底层实现
我们常用的SGI STL,如果没有指定底层实现的话,默认是以deque为缺省情况下栈的底层结构。
deque是一个双向队列,只要封住一段,只开通另一端就可以实现栈的逻辑了。
SGI STL中 队列底层实现缺省情况下一样使用deque实现的。
1.3 栈和队列基础操作
我们在创建的时候不指定便是默认使用deque,但也可以像如下指定vector构建栈:
std::stack > third; // 使用vector为底层容器的栈 队列中先进先出的数据结构,同样不允许有遍历行为,不提供迭代器, SGI STL中队列一样是以deque为缺省情况下的底部结构。
也可以指定list 为起底层实现,初始化queue的语句如下:
std::queue> third; // 定义以list为底层容器的队列 二、栈实现
2.1 成对元素操作
1. 有效的括号
有效的括号
代码实现:
class Solution {
public:
bool isValid(string s) {
stack tmp;
for(int i = 0; i < s.size(); i++){
if(s[i] == '{') tmp.push('}');
else if(s[i] == '(') tmp.push(')');
else if(s[i] == '[') tmp.push(']');
else if(!tmp.empty() &&tmp.top() == s[i])tmp.pop();
else if(tmp.empty() || s[i] != tmp.top()) return false;
}
return tmp.empty();
}
};
//错误1:栈为空时不能使用top()会导致未定义,需要用tmp.empty()来中和 2. 删除字符串中的所有相邻重复项
删除字符串中的所有相邻重复项
注意可以用数组模拟栈的操作,实现原地操作
代码实现1:
class Solution {
public:
string removeDuplicates(string s) {
stack tmp;
for(int i=0;i 代码实现2:
class Solution {
public:
string removeDuplicates(string S) {
string result;
for(char s : S) {
if(result.empty() || result.back() != s) {
result.push_back(s);
}
else {
result.pop_back();
}
}
return result;
}
};
2.2 在队尾进行操作
1.逆波兰表达式
逆波兰表达式求值
每次遇到运算符才计算,否则将表示数字的字符串直接push进入栈内(通过stio转换为int)
string s = "12345";
int num1 = stoi(s);如果进入计算,需要将最顶上两个取出来计算,因为算式都是两个数计算一次,然后将结果存入栈顶,下次要用就再取出来
代码实现:
lass Solution {
public:
int evalRPN(vector& tokens) {
stack tmp;
for(int i = 0; i < tokens.size(); i++){
if(tokens[i] == "*" || tokens[i] == "/" ||tokens[i] == "+" || tokens[i] == "-"){
long x = tmp.top();
tmp.pop();
int y = tmp.top();
tmp.pop();
if(tokens[i] == "*") tmp.push(y*x);
else if(tokens[i] == "/") tmp.push(y/x);
else if(tokens[i] == "+") tmp.push(y+x);
else tmp.push(y-x);
}else
tmp.push(stoi(tokens[i]));
}
return tmp.top();
}
};
//问题1:由于每个成员都是字符串,不能直接入栈也不能通过ascii码计算,此处引入stoi来将数字部分字符串转换为int型 三、队列实现
3.1 单调队列-滑动窗口中的最大值
滑动窗口中的最大值
重点:
我们只需要维护最大值即可,但由于当前的最大值(下述1操作)被pop掉后,后面留下的值不一定是剩下元素中的最大值,因此我们还有维护一个次大值,这样每次保证栈里面只有两个数就行(只存放一个数也会导致最大值被1操作pop掉后接下来进来的不是剩下元素的最大值)
由于需要维护两个值,次大值得从队尾更新,那么需要使用双端队列
设计单调队列的时候,pop,和push操作要保持如下规则:
- pop(value):如果窗口移除的元素value等于单调队列的出口元素,那么队列弹出元素,否则不用任何操作(如果不这样,会导致一个元素是最大值但不属于该窗口时,仍然会被留下)
- push(value):如果push的元素value大于入口元素的数值,那么就将队列入口的元素弹出,直到push元素的数值小于等于队列入口元素的数值为止
保持如上规则,每次窗口移动的时候,只要问que.front()就可以返回当前窗口的最大值。
代码实现:
(错误示例)
方法1:错误点在于单端队列无法保证队列元素为单调,那么当最大值被pop后,新得front不一定是剩下数里面的最大值
//方法1:错误点在于单端队列无法保证队列元素为单调,那么当最大值被pop后,新得front不一定是剩下数里面的最大值
class Solution {
public:
vector maxSlidingWindow(vector& nums, int k) {
queue tmp;
vector result(nums.size() - k + 1);//创建 result 向量时没有预先分配空间,所以在尝试访问 result[i - k + 1] 时会引发错误
for(int i=0;i tmp.front() || tmp.size() == k))tmp.pop();
if(tmp.empty() || (nums[i] <= tmp.front() && tmp.size() < k))tmp.push(nums[i]);
if(i>=k-1)result[i - k + 1] = tmp.front();
}
return result;
}
}; 正确示例:
//方法2:双端队列
class Solution {
public:
vector maxSlidingWindow(vector& nums, int k) {
deque tmp;
vector result(nums.size() - k + 1);
for(int i=0;i tmp.front()))tmp.pop_front();
while(!tmp.empty() && (nums[i] > tmp.back()))tmp.pop_back();
if(tmp.empty() || (nums[i] <= tmp.back() && tmp.size() <= k))tmp.push_back(nums[i]);
//<=k不能写为=k-1){
if(i>k-1 && nums[i-k] == tmp.front())tmp.pop_front();
result[i - k + 1] = tmp.front();
}
}
return result;
}
}; 3.2 优先级队列
1.合并 k 个有序链表
合并 K 个升序链表
2.前 K 个高频元素
前 K 个高频元素