点云配准ICP&NDT
NDT
简介
很多匹配算法需要在两帧数据之间进行特征匹配,例如ICP中会进行点到点、点到线、点到面的特征匹配,特征匹配的效果最终决定了点云配准的效果,而NDT不需要进行特征匹配。NDT是将第一帧点云转换至栅格地图,每个栅格计算其中点的正态分布,因此将第一帧点云转换为一个个栅格表示的分段连续可导的概率密度函数,使用正态分布概率密度函数描述点云的局部性质。然后将第二帧点云投影至栅格地图中,计算出第二帧点云在栅格地图中的概率,通过牛顿法找到最佳匹配位姿,使得第二帧点云投影至栅格地图后概率最大化,最终完成点云配准。
NDT的步骤可分为:建立第一帧点云的栅格地图,牛顿法迭代使得第二帧点云投影至栅格地图得到的概率最大化。
NDT优点:不需要进行点云之间的特征匹配,避免了特征匹配中出现的问题,例如点云噪声、物体移动、点云重合度对特征匹配的影响。使用正态分布概率密度函数描述点云的局部性质,因此所有导数都可以通过解析法求解,因此计算结果准确并且比较快。
建立栅格地图
NDT通过一系列栅格描述的本地点云正态分布描述整个点云的分布。首先将第一帧点云分割为等大的栅格,对于包含一定数量点的栅格,计算栅格内点坐标的均值以及方差,最终可以获得本栅格内点云的正态分布: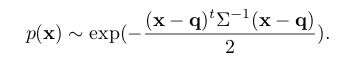
因此每个栅格描述了栅格中任意位置的概率密度。
实现细节
由于栅格地图将整个点云进行了离散化,在栅格与栅格之间会出现不连续的现象,可能会造成误差。为了避免离散化的影响,NDT会同时建立四个栅格地图,彼此相互错位半个栅格的长度,这四个栅格地图会同时参与计算,最终结果为四个栅格地图计算结果的和。
计算栅格地图内协方差矩阵时,为了避免协方差矩阵出现奇异性,如果协方差矩阵较大特征值远大于较小的特征值,则将较大特征值进行减小,最终计算得到协方差矩阵。
扫描匹配
首先根据里程计或者匀速运动模型得到先验位姿,根据先验位姿将第二帧点云投影至栅格地图中,对于第二帧点云中每个点,根据它所在的栅格计算概率密度,最终通过求和得到第二帧点云在栅格地图中的概率密度,点云位姿作为参数块,使用牛顿法找到这个概率密度的最大值,最终得到后验位姿。
由于使用正态分布概率密度函数描述点云的局部性质,因此概率密度函数的导数和偏导数可以通过解析法进行求解,所以可以计算出牛顿法中所需要的海塞矩阵和雅克比矩阵。
牛顿法迭代公式推导
第二帧点云在栅格地图中的概率密度为:
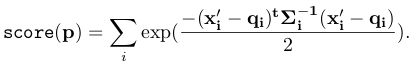
对概率密度取负号,通过牛顿法找到最小值。对于牛顿法每次迭代,需要求解增量方程:
![]()
因此需要求解海塞矩阵和雅克比矩阵,得到增量后更新位姿,不断迭代,直到增量位姿小于一定阈值,说明收敛。
对于点云中一点,他在栅格内关于均值的坐标为:
![]()
因此这个点的概率密度为:

通过链式求导,概率密度关于位姿的导数等于概率密度关于点激光点局部坐标的导数乘以激光点局部坐标有关位姿的导数,因此可得到雅克比矩阵
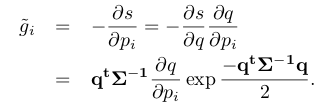
其中,激光点局部坐标有关位姿的导数为:
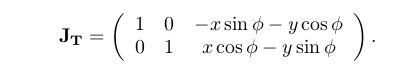
海塞矩阵:
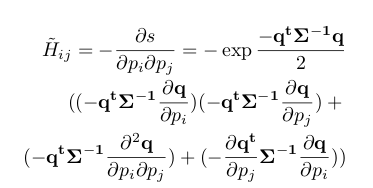
NDT算法特点:
- 不需要进行点云之间的特征匹配,避免了特征匹配中出现的问题。
- 使用正态分布概率密度函数描述点云的局部性质,因此所有导数都可以通过解析法求解,因此计算结果准确并且比较快。
- 可能存在的问题:点云是否可以通过局部正态分布描述?
ICP
简介
ICP通过迭代的方式,通过优化相对位姿,不断减小两帧点云之间点到点的距离,直到迭代收敛,最终计算出两帧点云的相对位姿。ICP分为特征匹配、位姿优化两个步骤。
由于无法像视觉SLAM提供准确的特征匹配关系,因此对于基于激光点云的经典ICP来说,使用点到点的最近距离进行特征匹配。使用ICP算法配准源点云和目标点云,对于源点云中每个点,找到它在目标点云中最近的点,如果这两个点的距离小于阈值,则将这两个点作为匹配点,计算出所有匹配点之后,最终可以获得源点云与目标点云的匹配关系。
获得两点云的匹配点之后,构建非线性最小二乘问题,参数块是两点云之间的相对位姿,残差是所有匹配点之间的距离的和,可以通过优化或者解析的方法计算最优位姿变换(例如基于SVD的解析方法),并不断进行特征匹配、位姿优化的迭代,直到满足收敛条件,最终计算出两点云的相对位姿。
位姿优化
公式推导思想
首先计算两点云的去质心坐标点云,然后两点云的旋转由去质心坐标点云求解,两点云的位移由经过旋转后的质心坐标求解,因此将将旋转和位移的求解分割为两个步骤。
详细推导
对于点云中每个匹配特征点,代价函数为:
![]()
由于两帧点云完成匹配后相互重合,因此两点云的质心坐标是相同的,因此首先计算两点云的质心坐标,然后计算出质心坐标下的两个点云
![]()

所以代价函数就成为质心坐标下的两点云匹配点的和:
![]()
所以将最小二乘问题转换为两步,首先根据质心坐标下的代价函数求得相对姿态,然后相对位置就是经过相对姿态变换后两点云坐标的差
![]()
计算
![]()
对H矩阵进行SVD分解,计算
![]()
如果行列式为1,说明X为相对姿态,然后求得相对位姿
SVD公式推导
思想
最后代价函数可转换为旋转矩阵与去质心坐标矩阵乘积的迹,由定理可知,正定矩阵的迹要大于任意正交矩阵乘以正定矩阵的迹,因此找到旋转矩阵R,可转换为正定矩阵的行驶,就求得了所需要的旋转矩阵。
对H矩阵进行SVD分解,取正交矩阵为SVD分解后的矩阵,然后回带,会发现转换为了正定矩阵的形式。
详细推导
质心坐标系下代价函数可写为
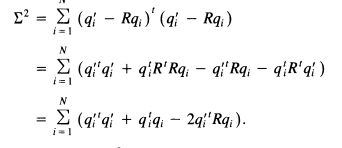
可以看到,最小化代价函数等价于最大化
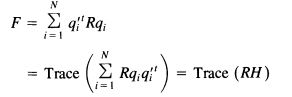
通过对H的SVD分解,可以得到
![]()
因此令R等于
![]()
即可求得非线性最小二乘问题的最小值
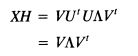
TODO:如何理解通过SVD求最大值?
ICP和NDT算法之间的优劣
ICP相比NDT,更容易受到初值误差的影响,当初始误差较大时,ICP更容易出现无法计算位姿的情况。
NDT相比ICP,旋转误差更大。因此ICP对旋转的约束更强,NDT对初始误差的健壮性更强。[1]
NDT的匹配速度要比ICP块,NDT的时间复杂度为O(N),其时间复杂度与点云的数量成正比,ICP的时间复杂度是O(NlogN),即通过KD树进行查找的时间复杂度。
由于ICP是进行点云中点到点的匹配,而NDT是将点云转换为分段连续的正态分布函数,因此NDT对动态物体干扰的抵抗力更强。
由于NDT对初始误差的敏感度较低,因此当速度较快时,运动方程无法提供准确的先验位姿,此时NDT的效果要由于ICP。
当环境中缺少垂直特征时,NDT相比ICP会提供更好的约束,原因是NDT使用栅格正态分布描述点云的局部性质,因此稀少的垂直特征可以体系在某些栅格的正态分布中,而ICP使用点云之间点到点的匹配,垂直点特征的影响会被大面积水平点特征减弱。[2]
[1]Evaluation_of_3D_registration_reliability_and_speed_-_A_comparison_of_ICP_and_NDT
[2]3D Scan Registration Based Localization for Autonomous Vehicles – A Comparison of NDT and ICP under Realistic Conditions
ICP要求点云的完全重合,这一假设会受到现实各种因素的影响。
点云配准不利因素
- 初始值误差
- 点云的不重合度
- 动态物体
传统ICP及其变体的比较
传统ICP的缺陷
由于经典ICP计算点云中点到点的距离,因此最小二乘期望的是两个点云的完全重合,然而现实环境中由于遮挡关系,两帧点云往往不是完全重合的,可能两帧点云只存在一部分的点是完全重合。由于点云实际上是现实几何环境的离散化表示,同时点云受到噪声的影响,即便在同一平面,离散化得到的点云也不可能完全相同,因此使用点到点的距离无法准确描述点云之间的配准问题。
点到面、点到线的距离解决了离散化问题。由于点云中的平面只提供了平面法向的约束,因此计算点到面的距离,只考虑平面法向约束,而避免了平面切向方向的影响。
改进的ICP——GICP和NICP
GICP是以概率的视角解决ICP问题,通过求解最大似然,求解出两点云的相对位姿,GICP充分地考虑了点附近的结构信息,因此可以在非线性优化过程中避免很多错误的匹配。
GICP的基本流程与ICP基本相同,首先通过KD树寻找欧式距离最小的点作为两点云之间的匹配。通过高斯分布的概率模型来描述每个激光点,计算出激光点的协方差矩阵,然后通过最大似然,构建出相应的非线性最小二乘问题,根据匹配点的各自的协方差,误差函数的距离进行加权,也就是通过协方差矩阵构建出的马氏距离,描述非线性最小二乘的误差。
计算协方差矩阵
通过KD树,找到该点附近的激光点,首先计算出激光点的均值,然后再计算协方差矩阵,由于GICP基于平面假设,认为点云是在连续平面上的离散采样,因此会对计算出的协方差矩阵进行SVD分解,通过修改奇异值为[1,1,小量],将该点的协方差矩阵修改为满足平面分布的协方差矩阵.
最大化似然,求解非线性最小二乘
优点
由于GICP充分考虑了点的局部平面性质,对于两对匹配激光点,通过其各自协方差矩阵的加权,只会在法线方向提供约束,也就是两点之间法线方向的距离会有较大的权重,平面方向权重很小。并且对于错误匹配点对,根据各自的协方差在非线性优化中加权,得到的权重较小,从而避免了错误匹配点对在非线性优化的影响,例如两个匹配点对各自的平面是相互垂直的,属于错误匹配,因此通过非线性优化加权,得到的权重较小。
