基于Python的股票红利预测
目的:数据文件data.csv是某股票从1997-2017的20年来各季度红利数据,找出时序数据的构成因素,并分别通过指数平滑法和自回归ARIMA模型方法,建立时序数据的预测模型,并预测下两年的红利(bonus)。
data.csv
❌注意:本文仅用于学习Python对时间序列数据的处理,不建议用于炒股决策!!!
1. 加载包
import pandas as pd
import numpy as np
from statsmodels.tsa import holtwinters as hw
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.graphics.tsaplots import plot_pacf
from statsmodels.graphics.gofplots import qqplot
import matplotlib.pyplot as plt
from statsmodels.tsa import arima_model
import warnings
2. 导入数据
f = open('实验4数据.csv')
mydata = pd.read_csv(f)
# print(mydata)
print(mydata.head())
3. 创建时序数据并绘图
ts = pd.period_range('1997/01', periods=len(mydata), freq='Q')
# 创建DF结构的数据,以ts为索引,以bonus为列名
bonus_data = pd.DataFrame(mydata['bonus'].values, index=ts, columns=['bonus'])
print(bonus_data.head())
# 显示所有的点
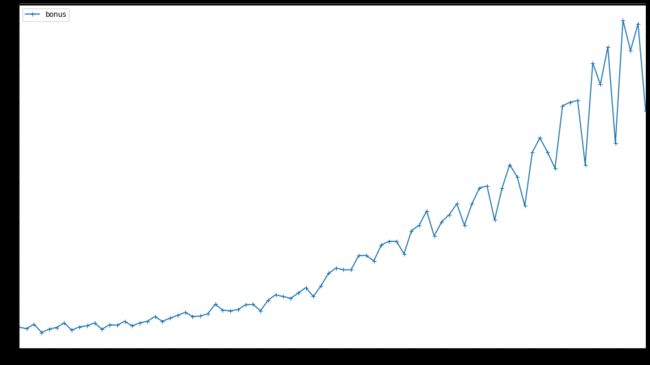
bonus_data.plot(style=['+-'], figsize=(16, 9))
4. 数据预处理
- 长期趋势:bonus(股票红利)随着时间变动呈上升趋势
- 季节变动:bonus(股票红利)在第四、一、二季度上升,在第三季度数值下降,并随着时间变化,呈现放大情况
# 数据对数化
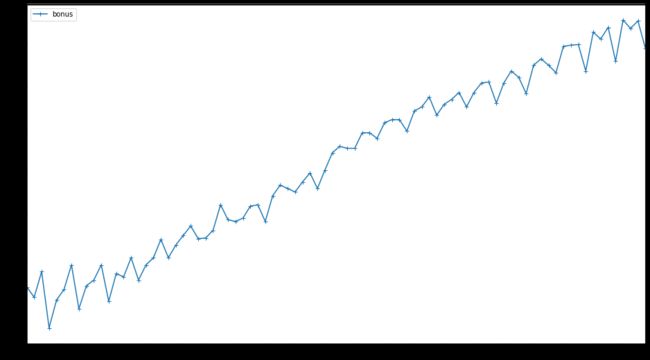
bonus_log = np.log(bonus_data)
bonus_log.plot(style='+-', figsize=(16, 9))
5. 建立模型–三次指数平滑法
一次指数平滑:适用于序列没有趋势和季节性特征
二次指数平滑:适用于序列有趋势特征但无季节性特征
三次指数平滑:适用于序列有趋势特征且有季节性特征
5.1 创建模型
# 长期趋势、季节趋势:add
# 季节周期:季度
# seasonal_periods:季度数据为4,月度数据的为12,周周期数据为7
# trend、seasonal为add,任取一个时间段,数据增量为0
bonus_hw = hw.ExponentialSmoothing(bonus_log, trend='add', seasonal='add', seasonal_periods=4)
hw_fit = bonus_hw.fit()
hw_fit.summary()
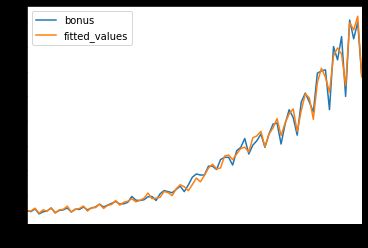
bonus_data.plot()
np.exp(hw_fit.fittedvalues).plot(label='fitted_values', legend=True)
5.2 残差图
plot_acf(hw_fit.resid)
5.3 残差(预测误差)的平稳性检验(单位根检验)
如果存在单位根,那么就是非平稳时间序列,会使回归分析中存在伪回归
第二项为p值,小于0.05。可以判定残差为平稳序列
adfuller(hw_fit.resid)
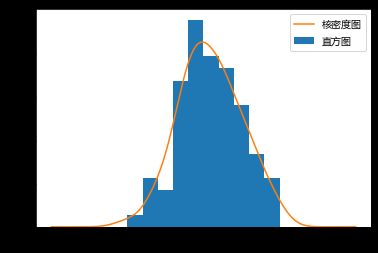
5.4 直方图+核密度图
核密度曲线类似于概率密度曲线,其曲线下的面积是1,因此其y轴上的单位通常是小于1的核密度分布值。
实质是一种对直方图的抽象。类似统计学中的频数分布图和概率密度函数的区别。
plt.figure()
# 需要注意的是:在直方图的基础上添加核密度图,必须将直方图的频数更改为频率,即density参数设置为True。
plt.hist(hw_fit.resid, density=True, label = '直方图')
hw_fit.resid.plot(kind='kde', label = '核密度图')
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']#处理中文乱码
plt.legend()# 显示图例
plt.show()
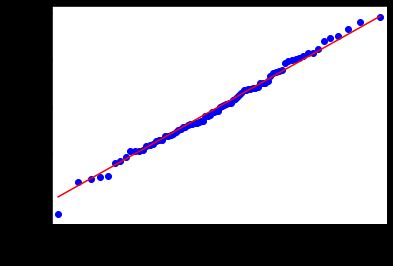
5.5 正态qq图
qqplot(hw_fit.resid, line='s')
根据qq图可知,残差服从正态分布,峰度小于3
5.6 预测
bonus_forecast = np.exp(hw_fit.predict(start='2018/1', end='2019/12'))
print(bonus_forecast)
bonus_data.plot()
bonus_forecast.plot(label='forecast', legend=True)
6. 自回归移动平均法
差分整合移动平均自回归模型(ARIMA) 是指将非平稳时间序列转化为平稳时间序列,然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。
ARIMA(p,d,q)中,AR是”自回归”,p为自回归项数;MA为”滑动平均”,q为滑动平均项数,d为使之成为平稳序列所做的差分次数(阶数)。
处理思路:
- 绘制数据随时间变化趋势,判断为平稳序列还是非平稳序列
- 若为非平稳序列,使用差分转化为平稳序列,得到参数d的取值
- 根据ACF、PACF寻找最优参数p、q
平稳序列:
基本上不存在趋势的序列,各观察值基本上在某个固定的水平上波动;或虽有波动,但并不存在某种规律,而其波动可以看成是随机的。
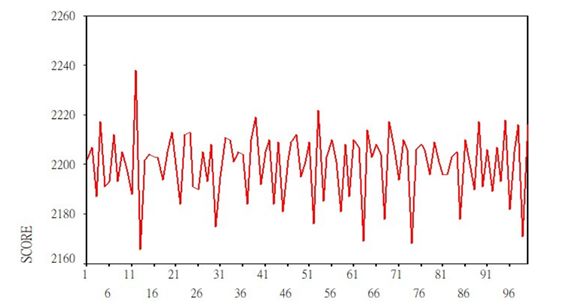
6.1 差分
差分,简单来说就是后一时间点的值减去当前时间点,也就是 y t − y t − 1 y_{t}-y_{t-1} yt−yt−1, 每做一次差分就少一个数据。
差分理解
# 一阶差分并去除空值
bonus_log_diff1 = bonus_log.diff().dropna()
bonus_log_diff1.plot()
# 可以看到通过 1 次差分数据已经平稳
adfuller(bonus_log_diff1['bonus'])
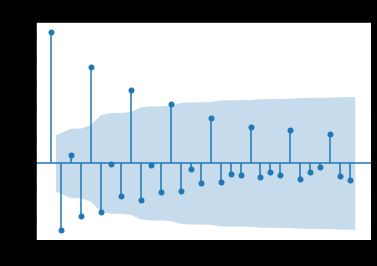
6.2 自相关图、偏自相关图
# 自相关图 拖尾
plot_acf(bonus_log_diff1, lags=30)
# 偏自相关图 拖尾
plot_pacf(bonus_log_diff1, lags=30)
6.3 确定模型参数
aic_values = []
find_index = ()
warnings.filterwarnings('ignore')
for p in range(8):
for q in range(8):
try:
myfit = arima_model.ARIMA(bonus_log, (p,1,q)).fit()
aic_values.append(myfit.aic)
print('(%d:%d,1,%d), AIC:%d' %(find_index, p, q, myfit.aic))
find_index += 1
except:
pass
print(aic_values.index(min(aic_values)), min(aic_values))
arima_fit = arima_model.ARIMA(bonus_log, (3,1,2)).fit()
arima_fit.summary()
6.4 单位根检验
# 平稳性检验
# plot_acf(arima_fit.resid)
adfuller(arima_fit.resid)
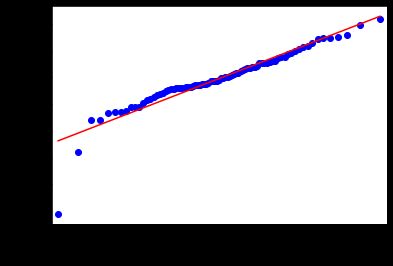
6.5 QQ图
qqplot(arima_fit.resid, line='s')
plt.figure()
plt.hist(arima_fit.resid, density=True)
arima_fit.resid.plot(kind='kde')
plt.show()
# 残差符合正态分布
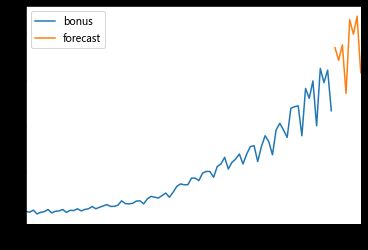
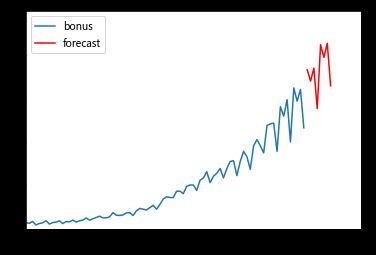
6.6 预测
bonus_forecast = np.exp(arima_fit.forecast(8)[0])
print(bonus_forecast)
plt.figure()
plt.plot(range(len(bonus_data)), bonus_data['bonus'], label='bonus')
plt.plot(range(len(bonus_data), len(bonus_data)+len(bonus_forecast)),
bonus_forecast, label='forecast', color='r')
plt.xlim(0, 100)
plt.ylim(0, 25)
plt.legend()
plt.show()
7. 比较两种模型的优劣
print('指数平滑法:AIC=%d, SSE=%.2f \n ARIMA模型:AIC=%d, SSE=%.2f' %(hw_fit.aic, sum(hw_fit.resid**2), arima_fit.aic, sum(arima_fit.resid**2)))