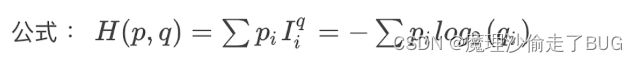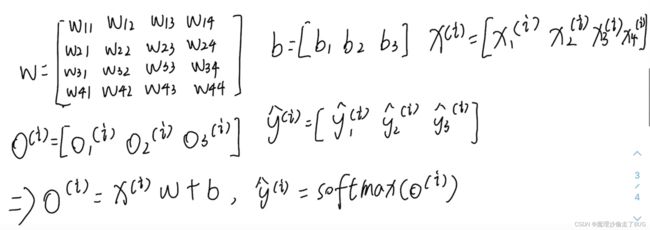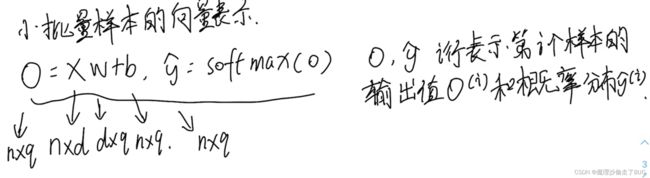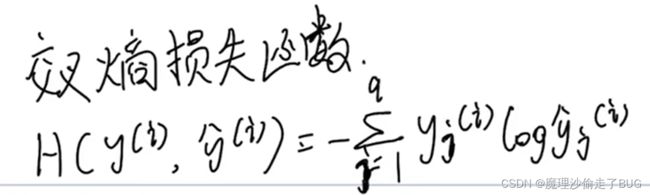【李沐深度学习笔记】Softmax回归
课程地址和说明
Softmax回归p1
本系列文章是我学习李沐老师深度学习系列课程的学习笔记，可能会对李沐老师上课没讲到的进行补充。
Softmax回归
虽然它名字叫作回归，但是它其实是分类问题
本节课的基础
想要学会本节课得需要一点基础，我真没看懂这节课讲的是什么，查了一些资料补了补基础
此处参考视频信息量 ｜熵 ｜ 交叉熵 ｜KL散度 （相对熵）｜交叉熵损失函数
信息量（Amount of Information）
定义
事件包含的信息量大小（事件发生的难度有多大)
- 小概率事件，它发生的难度比较大，所以有较大的信息量；
- 大概率事件，它发生的难度比较小，所以有较小的信息量。
【例】
公式
信息量的公式为：
I ( x ) : = （人为定义的） l o g 2 1 P ( x ) = − l o g 2 P ( x ) I(x):=（人为定义的）log_{2}{\frac{1}{P(x)}}=-log_{2}{{P(x)}} I(x):=（人为定义的）log2P(x)1=−log2P(x)
性质
对于独立事件 A , B A,B A,B，其概率为 P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) P(AB)=P(A)P(B)，而两个事件同时发生的信息量等于两个事件的信息量相加，即：
I ( A B ) = I ( A ) + I ( B ) I(AB)=I(A)+I(B) I(AB)=I(A)+I(B)
例子
熵（Entropy）
定义
【注】期望就是加权和求出来的平均值，此处权值为概率
公式
作用
【注】左图，每个概率都相等，不确定哪个会更容易发生，而右图很容易确定。
例子
结论
交叉熵
定义
公式
例子
结论
相对熵（KL散度）
KL散度以 Kullback 和Leibler的名字命名，也被称为相对嫡
作用
用于衡量2个概率分布之间的差异
公式
假设真实概率分布为 p p p、预测概率分布(估计概率分布)为 q q q
重要性质
交叉熵损失函数
Softmax回归的基本原理
此处参考视频：softmax回归原理及损失函数-跟李沐老师动手学深度学习
Softmax回归也是和线性回归一样讲数字特征和权重做线性叠加，不同的是线性回归的输出是一个连续的值，但Softmax回归的输出是离散的值，并且其输出由线性回归中的一个变为了多个：
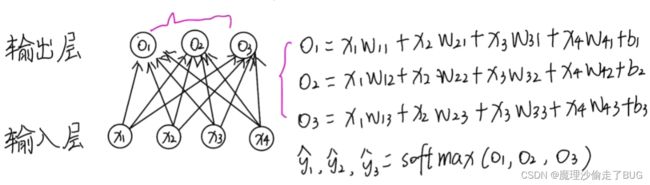
将特征和权重做叠加后用Softmax函数进行计算，将输出值 O 1 , O 2 , O 3 O_{1},O_{2},O_{3} O1,O2,O3映射为0到1之间的数（即概率， y i ^ \hat{y_{i}} yi^是概率值），公式如下：
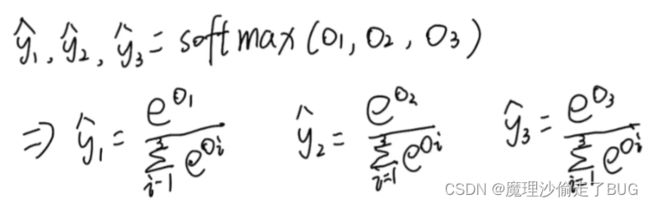
并且按此方法得到了一个概率分布，即预测值 y 1 ^ , y 2 ^ , y 3 ^ , . . . \hat {y_{1}},\hat {y_{2}},\hat {y_{3}},... y1^,y2^,y3^,...都为正值，并且它们的和为1
在实际操作中，我们选择 y 1 ^ , y 2 ^ , y 3 ^ , . . . \hat {y_{1}},\hat {y_{2}},\hat {y_{3}},... y1^,y2^,y3^,...中最大的预测值，找到最大的预测值所对应的类别标签即为我们预测的类别。
举个例子（下面认为输出类别是第二类）：
以上就是Softmax回归的预测过程。
为了提高计算效率，我们将上面的数学公式形式化为线性代数语言：
-
单个样本的向量形式：
-
小批量样本的向量形式
【注】如果行向量不能相乘或相加，默认取转置， n n n为 n n n个样本， d d d为数字特征的个数， q q q表示输出类别的个数
- 损失函数
对于概率分布问题，其损失函数一般为交叉熵损失函数：
【注】有一个为1，其他为0，其他项目都没了
从回归到多类分类
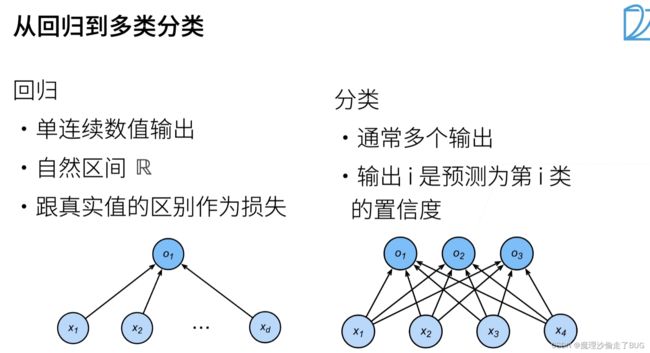
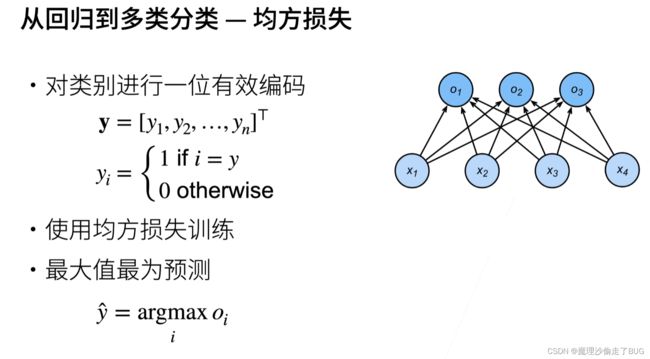
【注】 y i y_{i} yi有一个为1，说明该输出结果属于第 i i i个类别。
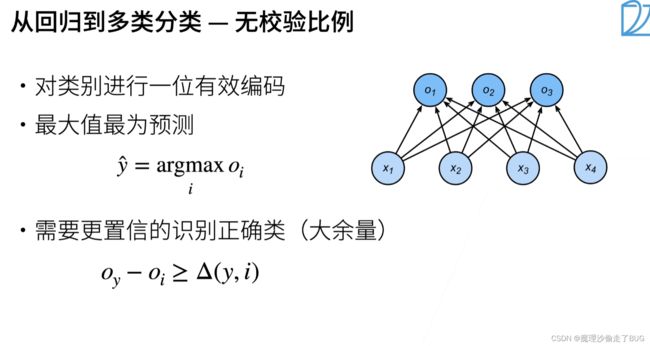
【注】正确类 O y O_{y} Oy的置信度要远远大于其他非置信度的 O i O_{i} Oi
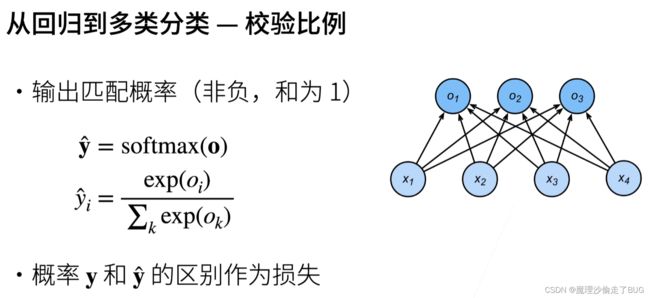
【注】 o → \overrightarrow{o} o是一个长度为 n n n的向量，前文提到的 o → = ( O 1 , O 2 , . . . ) \overrightarrow{o}=(O_{1},O_{2},...) o=(O1,O2,...)，这其中每一个 O i O_{i} Oi都是前文提到的线性回归。
比较两个概率之间的区别用交叉熵损失函数：
总结
