4、探索性数据分析
研究数据可以帮助确定您为数据分析考虑的统计技术是否合适。探索程序为所有病例或单独的病例组提供了各种可视化和数字的数据摘要。因变量必须(dependent variable)是尺度变量(scale variable),而分组变量可以是序数(ordinal)或名义变量(nominal)。
使用探索程序,可以:
•筛选数据
•识别异常值
•检查假设
•描述案例组之间的差异
组间描述性统计## 标题
例:黄曲霉毒素的浓度可以接受吗?
必须对玉米作物进行黄曲霉毒素检测,这种毒素的浓度在作物产量之间和作物产量之内存在很大差异。一个谷物加工者获得了8种作物产量,但是在接受它们之前,必须对黄曲霉毒素以十亿分之一的比例的分布情况进行评估。本例使用文件aflatoxin.sav。数据包括8种作物的16个样本。


在输出窗口里,双击描述性统计表,激活该表后会出现Pivot菜单(Pivot table透视表,简化的报表),就是下面黄色框框里的

选中“统计”,然后将它托到绿色底白色框里面
关闭透视托盘
通过在该表的边界之外单击来禁用该表

根据美国法律,如果黄曲霉毒素超过20ppb,其产出不宜供人类食用。从这个图表可以清楚地看出,在这些数据中,只有4,7,8的产量低于20 PPB的临界值
使用箱线图比较组## 标题
结果如下:
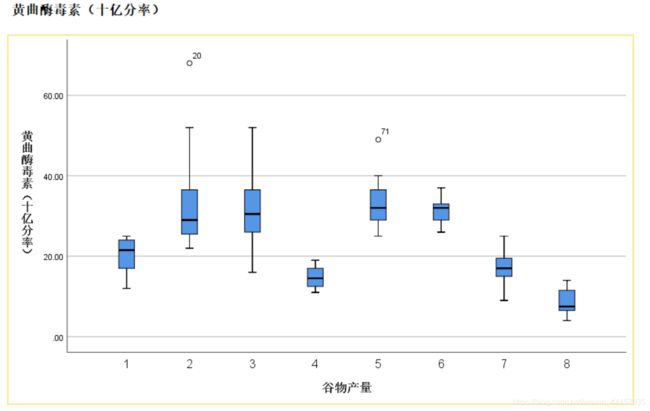
箱形图允许使用5个数字的摘要来比较每一组:中位数、第25和第75个百分位数,以及不具有统计学意义的最小和最大观察值。特别注意异常值和极值。
每个框内的粗黑线表示该分布的第50个百分位,或中位数。例如,yeild 1的黄曲霉素中值为21.50 PPB。注意,中位数在箱形图中有很大的变化。
上面和下面的横线,盒边界,分别表示25个和75个百分点的分布。对于yield 2,下边界为24.75,上边界为36.75。
yield 2有离群点20号,值是68,yield 5有离群点71号,值是49
极值会用*标出,在这些数据中没有极值
使用Explore程序,您创建了一个汇总表,显示了对于8个玉米产量中的5个来说,不安全的平均alfatoxin水平。您还创建了一个箱线图来可视化地确认这些结果。箱线图提供了任意数量组的快速、可视化摘要。此外,同一因素中的所有组排列在同一轴上,使比较更容易。55个箱线图提供了一些关于分布形状的证据,Explore过程提供了许多选项,允许更详细地查看组之间或与期望之间的差异。
Exploring Distributions
例:一家制造公司使用氮化银制造陶瓷轴承,这种轴承必须能承受1500摄氏度或更高的温度。众所周知,标准合金的耐热性是正态分布的。然而,一种新的高级合金正在测试中,它的分布是未知的。这个例子使用了ceramics.sav文件。
因为优质轴承的耐热性能是未知的,稳健的估计集中趋势和异常值表应该被要求。
“M-估计量”:用于估计位置的样本均值和中位数的稳健替代品。计算出的估计值适用于不同情况的权重不同。显示了Huber的m估计器、Andrews的波估计器、Hampel的重降m估计器和Tukey的双权重估计器
“离群值”:用大小写标签显示5个最大和5个最小的值。
“百分位数”:显示第5、第10、第25、第50、第75、第90和第95个百分比的值

点击“继续”,点击“图”。
你还应该请求对这些数据进行常态性测试。这些测试将针对每种合金分别计算

点击“继续”,点击“确定”
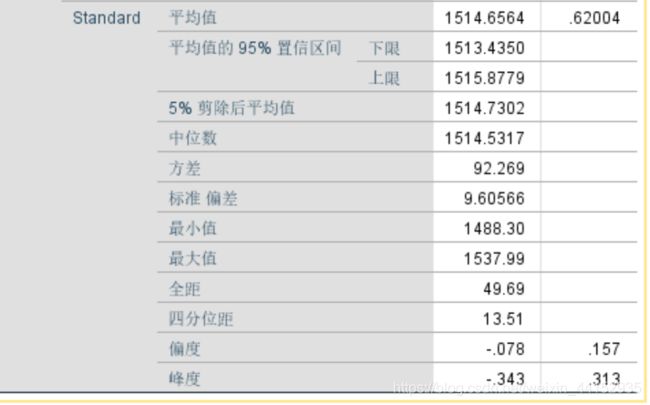
描述表是枢轴,以便合金是在层枢轴表,与标准轴承显示第一。均值、修剪均值和中位数接近相等,偏度和峰度统计量接近0。这有力地证明了标准轴承
的耐热性是正态分布的。

高级轴承则讲述了一个不同的故事。平均值高于修剪平均值或中位数;离群值或极值正拉着它向上。偏度和峰度统计也提供了在分布的上尾部的不均衡值的证据。

在这种情况下,对高级轴承的稳健估计非常接近中值(1539.72)。由于这些指标都不在平均值附近,这可能表明分布不是合理的正态分布。
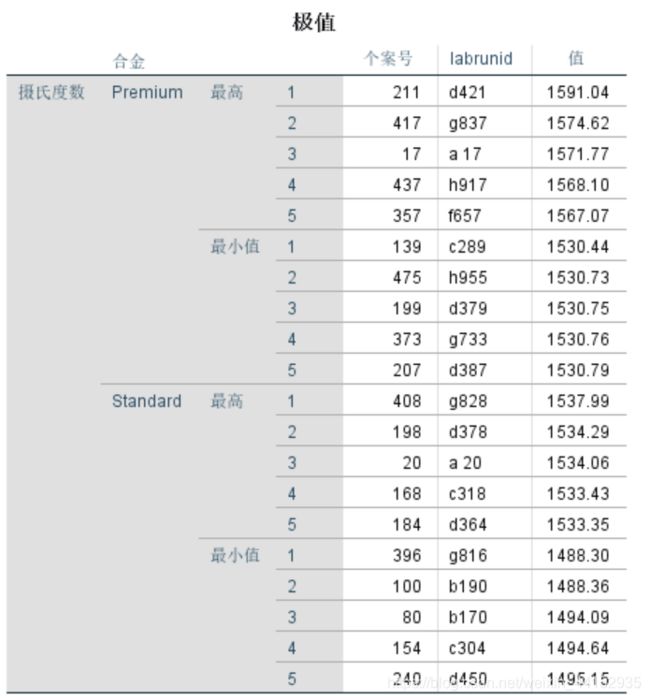
极值表列出了每个盟国的5个最高和最低值。溢价轴承范围从五个标准偏差以上到一个标准偏差低于平均值。有时,这些轴承可以承受比标准轴承高得多的高温,并且在1530摄氏度以下从不失效。
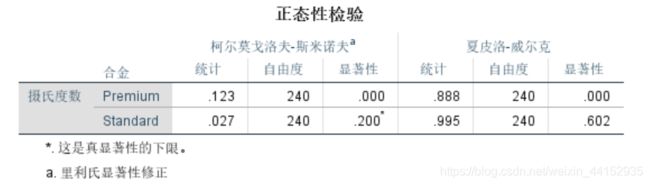
正态性检验在实际数据上覆盖一条正态曲线,以评估拟合程度。一个重要的测试意味着不适合。对于标准合金,测试结果不显著;它们很好地偏离了正态曲线。然而,对于高级合金,测试是重要的;它们很不符合正常曲线。

茎叶图使用原始数据值来显示
分布的形状。该图为高级轴承可视化正倾斜统计在描述表中看到;数值在1530 - 1543度范围内均匀聚集,然后在较高的温度下逐渐分散。
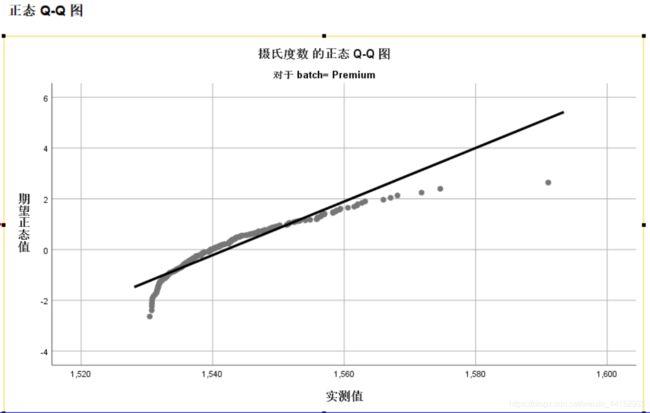
最后显示Q-Q图。图中的直线表示数据为正态分布时的期望值。观测到的溢价承载值明显偏离那条线,特别是当温度升高时。
Q-Q plot:将变量分布的分位数与多个测试分布的分位数绘制成图。概率图通常用于确定一个变量的分布是否与给定的分布匹配。如果选择的变量与测试分布相匹配,则点围绕一条直线聚类。
总结
使用探索程序,你发现高级合金有不同的分布与标准合金。值得肯定的是,新合金的平均耐热性比标准合金要高得多。不幸的是,有证据表明,平均值可能不是高级合金集中趋势的良好衡量标准。然而,60个集中趋势的稳健估计再次证实了高级合金的优越性。探索程序是一个非常有用的程序,在视觉上和数字上比较组,总结分布,检查正态假设,并寻找外围观察。在不观察数据的情况下,很容易假设数据没有异常值、极值或分布问题。幸运的是,Explore过程可以很容易地看出数据是如何验证这些假设的。•如果你的因变量是绝对的,尝试交叉检查程序。•其他程序允许您分层分组变量,以便您可以检查总结统计交叉分类的因素。有关更多信息,请参阅主题“总结过程”。有关更多信息,请参阅“方法过程”主题。有关更多信息,请参阅主题OLAP多维数据集过程。•你可以交替使用单样本Kolmogorov-Smirnov检验来检验你的因变量是否正态。这个过程还允许你根据泊松分布、均匀分布或指数分布检查你的因变量