Python中小波工具（pywt）分析EEG数据

小波作为一种信号处理的工具在脑波分析中应用很多，常用的有连续小波变换、小波包分析等等。小波涉及的相关介绍和公式推导有很多资料，文章末尾推荐了几个链接。本文主要介绍连续小波变换，小波包分解重构，对应频段能量计算这3种应用在Python中的实现。

文中的数据和代码参考：https://download.csdn.net/download/zhoudapeng01/12566856

数据来源为BCI竞赛公开数据集中的部分数据，剔除了无效数据。有关数据的描述见链接：

https://blog.csdn.net/zhoudapeng01/article/details/103822321

https://blog.csdn.net/zhoudapeng01/article/details/103893014

1、连续小波变换（主要用于时频域分析）

这里使用连续小波变换进行时频域分析，数据只是示例，代码中的参数在实际应用的时候需要根据实际情况进行调整。代码中有关小波尺度的计算很有意思，这里单独拿出来详细说明下。

一般用小波的尺度来衡量小波的频率，两者之间的转换关系为：

其中Fs为采样频率，wcf为小波的中心频率。

我们以下文代码中的参数为例，当一共想要分析totalscal个频率的时候，第i个频率对应的是，带入上面的等式中

该部分对应的代码如下：

import numpy as np
import matplotlib.pyplot as plt
import pywt
import mne
mne.set_log_level(False)
######################################################连续小波变换##########
# totalscal小波的尺度，对应频谱分析结果也就是分析几个（totalscal-1）频谱
def TimeFrequencyCWT(data,fs,totalscal,wavelet='cgau8'):
    # 采样数据的时间维度
    t = np.arange(data.shape[0])/fs
    # 中心频率
    wcf = pywt.central_frequency(wavelet=wavelet)
    # 计算对应频率的小波尺度
    cparam = 2 * wcf * totalscal
    scales = cparam/np.arange(totalscal, 1, -1)
    # 连续小波变换
    [cwtmatr, frequencies] = pywt.cwt(data, scales, wavelet, 1.0/fs)
    # 绘图
    plt.figure(figsize=(8, 4))
    plt.subplot(211)
    plt.plot(t, data)
    plt.xlabel(u"time(s)")
    plt.title(u"Time spectrum")
    plt.subplot(212)
    plt.contourf(t, frequencies, abs(cwtmatr))
    plt.ylabel(u"freq(Hz)")
    plt.xlabel(u"time(s)")
    plt.subplots_adjust(hspace=0.4)
    plt.show()


if __name__ == '__main__':
    # 读取筛选好的epoch数据
    epochsCom = mne.read_epochs(r'F:\BaiduNetdiskDownload\BCICompetition\BCICIV_2a_gdf\Train\Fif\A02T_epo.fif')
    dataCom = epochsCom[10].get_data()[0][0]
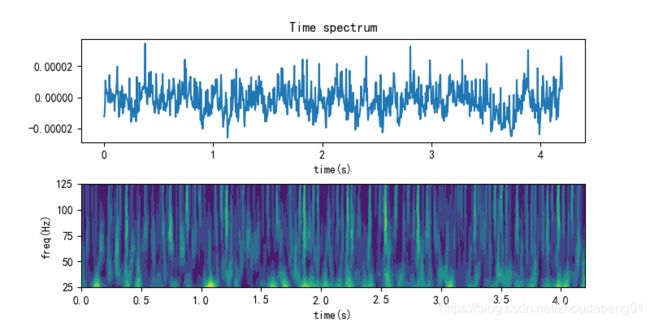
    TimeFrequencyCWT(dataCom, fs=250, totalscal=10, wavelet='cgau8')

对应结果如下，这里只是示例，并不进行分析。

2、小波包分解重构

小波包分解可以同时分析低频和高频部分的数据，分析结果的频率分辨率和小波树的深度有关，在使用的时候建议输入的数据个数最好为2的次方（如果不是2的次方重构后数据点数可能会和原始数据不同）。小波树节点的排序非常重要需要注意，在默认情况下并非由低频向高频排列。以深度为3的小波树为例，默认的节点排序为：['aaa', 'aad', 'ada', 'add', 'daa', 'dad', 'dda', 'ddd']，但是其对应频率由低到高的排序应为：['aaa', 'aad', 'add', 'ada', 'dda', 'ddd', 'dad', 'daa']。程序中使用了一种判断方法，可以判断分析目标频率对应的小波参数，不足之处就是如果分析的目标频率的范围较低，受小波分析的分辨率限制，小波树的深度就要加深。具体小波深度的选取要结合采样频率，数据点数，分析目标频率的范围等因素综合考虑来确定。

对应的示例代码如下：

import numpy as np
import matplotlib.pyplot as plt
import pywt
import mne

# 需要分析的四个频段
iter_freqs = [
    {'name': 'Delta', 'fmin': 0, 'fmax': 4},
    {'name': 'Theta', 'fmin': 4, 'fmax': 8},
    {'name': 'Alpha', 'fmin': 8, 'fmax': 13},
    {'name': 'Beta', 'fmin': 13, 'fmax': 35},
]

plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
mne.set_log_level(False)
########################################小波包变换-重构造分析不同频段的特征(注意maxlevel，如果太小可能会导致)#########################
def TimeFrequencyWP(data, fs, wavelet, maxlevel = 8):
    # 小波包变换这里的采样频率为250，如果maxlevel太小部分波段分析不到
    wp = pywt.WaveletPacket(data=data, wavelet=wavelet, mode='symmetric', maxlevel=maxlevel)
    # 频谱由低到高的对应关系，这里需要注意小波变换的频带排列默认并不是顺序排列，所以这里需要使用’freq‘排序。
    freqTree = [node.path for node in wp.get_level(maxlevel, 'freq')]
    # 计算maxlevel最小频段的带宽
    freqBand = fs/(2**maxlevel)
    #######################根据实际情况计算频谱对应关系，这里要注意系数的顺序
    # 绘图显示
    fig, axes = plt.subplots(len(iter_freqs)+1, 1, figsize=(10, 7), sharex=True, sharey=False)
    # 绘制原始数据
    axes[0].plot(data)
    axes[0].set_title('原始数据')
    for iter in range(len(iter_freqs)):
        # 构造空的小波包
        new_wp = pywt.WaveletPacket(data=None, wavelet=wavelet, mode='symmetric', maxlevel=maxlevel)
        for i in range(len(freqTree)):
            # 第i个频段的最小频率
            bandMin = i * freqBand
            # 第i个频段的最大频率
            bandMax = bandMin + freqBand
            # 判断第i个频段是否在要分析的范围内
            if (iter_freqs[iter]['fmin']<=bandMin and iter_freqs[iter]['fmax']>= bandMax):
                # 给新构造的小波包参数赋值
                new_wp[freqTree[i]] = wp[freqTree[i]].data
        # 绘制对应频率的数据
        axes[iter+1].plot(new_wp.reconstruct(update=True))
        # 设置图名
        axes[iter+1].set_title(iter_freqs[iter]['name'])
    plt.show()


if __name__ == '__main__':
    # 读取筛选好的epoch数据
    epochsCom = mne.read_epochs(r'F:\BaiduNetdiskDownload\BCICompetition\BCICIV_2a_gdf\Train\Fif\A02T_epo.fif')
    dataCom = epochsCom[10].get_data()[0][0][0:1024]
    TimeFrequencyWP(dataCom,250,wavelet='db4', maxlevel=8)

重构后的脑波数据如下：看着还像那么回事，实际上如果你输入的数据长度再长一些，看起来效果会好点。

3、基于小波包分解计算不同频段的能量和

计算能量或者说是功率的方法有很多，比如之前写过的PSD:https://blog.csdn.net/zhoudapeng01/article/details/106906593

这里利用小波包的方法计算区间能量的累加和。

对应的代码如下：

import numpy as np
import matplotlib.pyplot as plt
import pywt
import mne

# 需要分析的四个频段
iter_freqs = [
    {'name': 'Delta', 'fmin': 0, 'fmax': 4},
    {'name': 'Theta', 'fmin': 4, 'fmax': 8},
    {'name': 'Alpha', 'fmin': 8, 'fmax': 13},
    {'name': 'Beta', 'fmin': 13, 'fmax': 35},
]

plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
mne.set_log_level(False)
#############################################小波包计算四个频段的能量分布
def WPEnergy(data, fs, wavelet, maxlevel=6):
    # 小波包分解
    wp = pywt.WaveletPacket(data=data, wavelet=wavelet, mode='symmetric', maxlevel=maxlevel)
    # 频谱由低到高的对应关系，这里需要注意小波变换的频带排列默认并不是顺序排列，所以这里需要使用’freq‘排序。
    freqTree = [node.path for node in wp.get_level(maxlevel, 'freq')]
    # 计算maxlevel最小频段的带宽
    freqBand = fs / (2 ** maxlevel)
    # 定义能量数组
    energy = []
    # 循环遍历计算四个频段对应的能量
    for iter in range(len(iter_freqs)):
        iterEnergy = 0.0
        for i in range(len(freqTree)):
            # 第i个频段的最小频率
            bandMin = i * freqBand
            # 第i个频段的最大频率
            bandMax = bandMin + freqBand
            # 判断第i个频段是否在要分析的范围内
            if (iter_freqs[iter]['fmin'] <= bandMin and iter_freqs[iter]['fmax'] >= bandMax):
                # 计算对应频段的累加和
                iterEnergy += pow(np.linalg.norm(wp[freqTree[i]].data, ord=None), 2)
        # 保存四个频段对应的能量和
        energy.append(iterEnergy)
    # 绘制能量分布图
    plt.plot([xLabel['name'] for xLabel in iter_freqs], energy, lw=0, marker='o')
    plt.title('能量分布')
    plt.show()


if __name__ == '__main__':
    # 读取筛选好的epoch数据
    epochsCom = mne.read_epochs(r'F:\BaiduNetdiskDownload\BCICompetition\BCICIV_2a_gdf\Train\Fif\A02T_epo.fif')

    dataCom = epochsCom[10].get_data()[0][0]
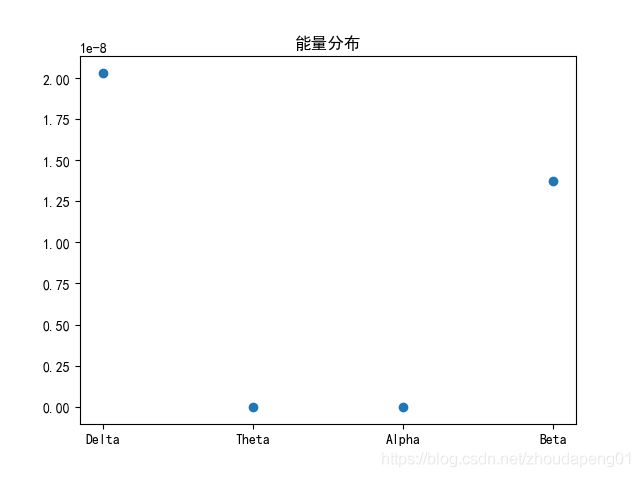
    WPEnergy(dataCom, fs=250, wavelet='db4', maxlevel=6)

计算结果：

 

参考资料

文中对应的数据和代码：

https://download.csdn.net/download/zhoudapeng01/12566856

小波变换：

https://www.cnblogs.com/jfdwd/p/9249850.html

https://blog.csdn.net/weixin_42943114/article/details/89603208

https://my.oschina.net/u/4335157/blog/3893295

小波包变换：

http://blog.sina.com.cn/s/blog_8fc890a20101ecn7.html

https://blog.csdn.net/zds13257177985/article/details/102896041

小波与小波包的区别：

https://blog.csdn.net/cqfdcw/article/details/84995904?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-2.nonecase&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-2.nonecase