Leetcode刷题笔记——剑指offer II （四）【队列、树】

队列

剑指 Offer II 041. 滑动窗口的平均值

给定一个整数数据流和一个窗口大小，根据该滑动窗口的大小，计算滑动窗口里所有数字的平均值。

实现 MovingAverage 类：

MovingAverage(int size) 用窗口大小 size 初始化对象。
double next(int val) 成员函数 next 每次调用的时候都会往滑动窗口增加一个整数，请计算并返回数据流中最后 size 个值的移动平均值，即滑动窗口里所有数字的平均值。
 

示例：

输入：
inputs = ["MovingAverage", "next", "next", "next", "next"]
inputs = [[3], [1], [10], [3], [5]]
输出：
[null, 1.0, 5.5, 4.66667, 6.0]

解释：
MovingAverage movingAverage = new MovingAverage(3);
movingAverage.next(1); // 返回 1.0 = 1 / 1
movingAverage.next(10); // 返回 5.5 = (1 + 10) / 2
movingAverage.next(3); // 返回 4.66667 = (1 + 10 + 3) / 3
movingAverage.next(5); // 返回 6.0 = (10 + 3 + 5) / 3
 

提示：

1 <= size <= 1000
-105 <= val <= 105
最多调用 next 方法 104 次

我的方法：队列，维护一个整数变量SUM
由题意，我们需要一个 先进先出 的数据结构——queue

class MovingAverage {
public:
	queue<int> q;
	int size;
	int sum = 0;
	/** Initialize your data structure here. */
	MovingAverage(int size):size(size) {

	}

	double next(int val) {
		if (q.size() < size) {
			q.push(val);
			sum += val;
		}
		else {
			sum -= q.front(); q.pop();
			sum += val; q.push(val);
		}
		return 1.0 * sum / q.size();
	}
};

（单调队列）剑指 Offer 59 - I. 滑动窗口的最大值

给定一个数组 nums 和滑动窗口的大小 k，请找出所有滑动窗口里的最大值。

示例:

输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7] 
解释: 

  滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7
 

提示：

你可以假设 k 总是有效的，在输入数组 不为空 的情况下，1 ≤ k ≤ nums.length。

思路一：优先队列 复杂度 $O(nlogk)$

思路：单调队列，deque 复杂度 $O(n)$
维护一个deque，使得deque中的元素单调
值得注意的是（），出队的判断：由于队列中的元素索引无法与原数组对应上，我们使用数值判断是否到达当前值q[0]==nums[i-k]

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        from collections import deque
        q = deque()
        ans = []
        for i, val in enumerate(nums):
            if i>=k and q and q[0]==nums[i-k]: # 
                q.popleft()
            while q and q[-1]<val:
                q.pop()
            q.append(val)
            if i>=k-1:
                ans.append(q[0])
        return ans

树

树的存储

（先序）剑指 Offer II 048. 序列化与反序列化二叉树

序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。

请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

示例 1：



输入：root = [1,2,3,null,null,4,5]
输出：[1,2,3,null,null,4,5]
示例 2：

输入：root = []
输出：[]
示例 3：

输入：root = [1]
输出：[1]
示例 4：

输入：root = [1,2]
输出：[1,2]
 

提示：

输入输出格式与 LeetCode 目前使用的方式一致，详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式，也可以采用其他的方法解决这个问题。
树中结点数在范围 [0, 104] 内
-1000 <= Node.val <= 1000

思路一：堆式存储 (空间占比太大)
当树的深度比较低时（低于16层，否则data数组会爆炸），可以采用该方式保存满二叉树

class Codec:
    def serialize(self, root):
        """Encodes a tree to a single string.

        :type root: TreeNode
        :rtype: str
        """
        data = [1001]*(int(10**6))
        def dfs(root: TreeNode, idx: int):
            if not root or idx>=len(data):
                return
            data[idx] = root.val
            dfs(root.left, idx<<1)
            dfs(root.right, idx*2 + 1)
        dfs(root, 1)
        return ",".join(map(str, data))

    def deserialize(self, data):
        """Decodes your encoded data to tree.

        :type data: str
        :rtype: TreeNode
        """
        data = list(map(int, data.split(",")))
        if data[1]==1001:
            return None
        def dfs(root: TreeNode, idx: int):
            left = idx<<1
            right = left + 1
            if left<len(data) and data[left]!=1001:
                root.left = TreeNode(data[left])
                dfs(root.left, left)
            if right<len(data) and data[right]!=1001:
                root.right = TreeNode(data[right])
                dfs(root.right, right)
            return None
        root = TreeNode(data[1])
        dfs(root, 1)
        return root

思路二：DFS，先序遍历

1. serialize(self, root)：直接利用本身定义，序列化左子树、右子树，返回 【根，左，右】即可
2. deserialize(self, data)：每次我们需要从先序遍历数组中找到根节点，因此需要利用 队列 pop 第一个元素

from collections import deque
class Codec:

    def serialize(self, root):
        """Encodes a tree to a single string.

        :type root: TreeNode
        :rtype: str
        """
        if not root:
            return "#"
        left = self.serialize(root.left)
        right = self.serialize(root.right)
        return str(root.val) + ',' + left + ',' + right

    def deserialize(self, data):
        """Decodes your encoded data to tree.

        :type data: str
        :rtype: TreeNode
        """
        if not data:
            return
        data = data.split(',')
        dq = deque(data)
        def dfs(dq: deque):
            val = dq.popleft() # 根节点
            if val=="#":
                return None
            root = TreeNode(int(val))
            root.left = dfs(dq)
            root.right = dfs(dq)
            return root
        return dfs(dq)

BFS 遍历

剑指 Offer II 043. 往完全二叉树添加节点

完全二叉树是每一层（除最后一层外）都是完全填充（即，节点数达到最大，第 n 层有 2n-1 个节点）的，并且所有的节点都尽可能地集中在左侧。

设计一个用完全二叉树初始化的数据结构 CBTInserter，它支持以下几种操作：

CBTInserter(TreeNode root) 使用根节点为 root 的给定树初始化该数据结构；
CBTInserter.insert(int v) 向树中插入一个新节点，节点类型为 TreeNode，值为 v 。使树保持完全二叉树的状态，并返回插入的新节点的父节点的值；
CBTInserter.get_root() 将返回树的根节点。

示例 1：

输入：inputs = ["CBTInserter","insert","get_root"], inputs = [[[1]],[2],[]]
输出：[null,1,[1,2]]
示例 2：

输入：inputs = ["CBTInserter","insert","insert","get_root"], inputs = [[[1,2,3,4,5,6]],[7],[8],[]]
输出：[null,3,4,[1,2,3,4,5,6,7,8]]
 

提示：

最初给定的树是完全二叉树，且包含 1 到 1000 个节点。
每个测试用例最多调用 CBTInserter.insert  操作 10000 次。
给定节点或插入节点的每个值都在 0 到 5000 之间。

我的方法：BFS遍历，额外队列存左右子节点不全存在的父节点

class CBTInserter {
public:
	TreeNode* root;
	queue<TreeNode*> q;
	CBTInserter(TreeNode* node): root(node) {
		queue<TreeNode*> tmp;
		tmp.push(node);
		while (!tmp.empty()) {
			int n = tmp.size();
			for (int i = 0; i < n; i++) {
				node = tmp.front(); tmp.pop();
				if (node->left) tmp.push(node->left);
				if (node->right)  tmp.push(node->right);
				if (!node->left || !node->right) q.push(node);
			}
		}
	}

	int insert(int v) {
		TreeNode* tmp = new TreeNode(v), *cur;
		if (q.front()->left && q.front()->right) q.pop();
		cur = q.front();
		if (!cur->left) {
			cur->left = tmp;
		}
		else if (!cur->right) {
			cur->right = tmp;
		}
		q.push(tmp);
		return cur->val;
	}

	TreeNode* get_root() {
		return root;
	}
};

剑指 Offer II 045. 二叉树最底层最左边的值

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。

假设二叉树中至少有一个节点。

示例 1:



输入: root = [2,1,3]
输出: 1
示例 2:



输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7
 

提示:

二叉树的节点个数的范围是 [1,104]
-231 <= Node.val <= 231 - 1 
 

我的方法：BFS，＋只存当前层的值的数组

int findBottomLeftValue(TreeNode* root) {
	queue<TreeNode*> q;
	q.push(root);
	vector<int> ans;
	while (!q.empty()) {
		int n = q.size();
		ans.clear();
		for (int i = 0; i < n; i++) {
			TreeNode* cur = q.front(); q.pop();
			ans.push_back(cur->val);
			if (cur->left) q.push(cur->left);
			if (cur->right) q.push(cur->right);
		}
	}
	return ans[0];
}

优化：只存一个整数（i==0时）的cur->val

剑指 Offer II 046. 二叉树的右侧视图

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1:



输入: [1,2,3,null,5,null,4]
输出: [1,3,4]
示例 2:

输入: [1,null,3]
输出: [1,3]
示例 3:

输入: []
输出: []
 

提示:

二叉树的节点个数的范围是 [0,100]
-100 <= Node.val <= 100 

BFS，加if判断

vector<int> rightSideView(TreeNode* root) {
	if (!root) return {};
	queue<TreeNode*> q;
	q.push(root);
	vector<int> ans;
	while (!q.empty()) {
		int n = q.size();
		for (int i = 0; i < n; i++) {
			TreeNode* cur = q.front(); q.pop();
			if (i==n-1) ans.push_back(cur->val);
			if (cur->left) q.push(cur->left);
			if (cur->right) q.push(cur->right);
		}
	}
	return ans;
}

（堆式存储记录法）662. 二叉树最大宽度

给你一棵二叉树的根节点 root ，返回树的 最大宽度 。

树的 最大宽度 是所有层中最大的 宽度 。

每一层的 宽度 被定义为该层最左和最右的非空节点（即，两个端点）之间的长度。将这个二叉树视作与满二叉树结构相同，两端点间会出现一些延伸到这一层的 null 节点，这些 null 节点也计入长度。

题目数据保证答案将会在 32 位 带符号整数范围内。

示例 1：

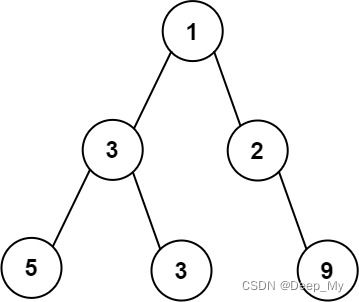
输入：root = [1,3,2,5,3,null,9]
输出：4
解释：最大宽度出现在树的第 3 层，宽度为 4 (5,3,null,9) 。

示例 2：

输入：root = [1,3,2,5,null,null,9,6,null,7]
输出：7
解释：最大宽度出现在树的第 4 层，宽度为 7 (6,null,null,null,null,null,7) 。

示例 3：

输入：root = [1,3,2,5]
输出：2
解释：最大宽度出现在树的第 2 层，宽度为 2 (3,2) 。
 

提示：

树中节点的数目范围是 [1, 3000]
-100 <= Node.val <= 100

BFS遍历
每次入队时，将当前节点的堆式存储索引也记录下来
例如：heap = [0, 根节点, 左子树，右子树，..., ]
使用临时数组 tmp 记录每一层的索引，tmp[-1]-tmp[0]+1 即为当前层的宽度

class Solution:
    def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int:
        from queue import Queue
        q = Queue()
        q.put((root, 1)) 						# 根节点索引
        ans = 0
        while not q.empty():
            n = q.qsize()
            tmp = []
            for i in range(n):
                cur, idx = q.get()
                tmp.append(idx)
                if cur.left:
                    q.put((cur.left, idx*2))	# 左子树
                if cur.right:
                    q.put((cur.right, idx*2+1))	# 右子树
            ans = max(tmp[-1]-tmp[0]+1, ans)
        return ans

DFS 遍历 （自顶向下，非自顶向下）

def dfs(params): { return }

• params用于传递dfs递归时的参数，（例如根节点向下计数）
• return用于返回 函数出栈时的数值（例如从叶节点向上计数），

根据题目情况去考虑运用二者

（后序遍历+剪枝）剑指 Offer II 047. 二叉树剪枝

给定一个二叉树 根节点 root ，树的每个节点的值要么是 0，要么是 1。请剪除该二叉树中所有节点的值为 0 的子树。

节点 node 的子树为 node 本身，以及所有 node 的后代。

示例 1:

输入: [1,null,0,0,1]
输出: [1,null,0,null,1] 
解释: 
只有红色节点满足条件“所有不包含 1 的子树”。
右图为返回的答案。


示例 2:

输入: [1,0,1,0,0,0,1]
输出: [1,null,1,null,1]
解释: 


示例 3:

输入: [1,1,0,1,1,0,1,0]
输出: [1,1,0,1,1,null,1]
解释: 


提示:

二叉树的节点个数的范围是 [1,200]
二叉树节点的值只会是 0 或 1

我的方法：dfs+哑结点
// 由于我写的dfs中，只会对left，right子节点进行剪枝，当根节点不满足要求时，无法考虑到，故使用了哑结点。
当dfsPruneTree 返回 true时，表明当前需要剪枝，即该节点的子树全是0

bool dfsPruneTree(TreeNode* root) {
	if (!root) return true;
	bool left = dfsPruneTree(root->left);
	bool right = dfsPruneTree(root->right);
	if (left) root->left = nullptr; // 
	if (right) root->right = nullptr;// 
	return !(!left || !right || root->val==1);
}
TreeNode* pruneTree(TreeNode* root) {
    TreeNode* tmp = new TreeNode(1);// 
    tmp->left = root;// 
	dfsPruneTree(tmp);
	return tmp->left;// 
}

（后序）669. 修剪二叉搜索树

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：


输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]
示例 2：


输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]
 

提示：

树中节点数在范围 [1, 104] 内
0 <= Node.val <= 104
树中每个节点的值都是 唯一 的
题目数据保证输入是一棵有效的二叉搜索树
0 <= low <= high <= 104

我的思路：dfs
首先想明白，函数dfs的作用是什么：返回该结点下，符合条件的子树结构。

class Solution {
public:
	TreeNode* dfs(TreeNode* root, int low, int high){
		if (root==nullptr){
			return nullptr;
		}
		TreeNode* resL, *resR;	
		resL = dfs(root->left, low, high);   // 符合条件的左子树
		resR = dfs(root->right, low, high);	 // 符合条件的右子树

		if (root->val<low){					// 当前节点不符合条件时
			return resR;
		}
		if (root->val>high){				// 当前节点不符合条件时
			return resL;
		}
		root->left = resL;					// 当前节点符合条件时
		root->right = resR;
		return root;		
	}

    TreeNode* trimBST(TreeNode* root, int low, int high) {
        TreeNode* ans = dfs(root, low, high);
		return ans;
    }
};

（后序遍历）剑指 Offer II 049. 从根节点到叶节点的路径数字之和

给定一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。

每条从根节点到叶节点的路径都代表一个数字：

例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。

示例 1：


输入：root = [1,2,3]
输出：25
解释：
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此，数字总和 = 12 + 13 = 25
示例 2：


输入：root = [4,9,0,5,1]
输出：1026
解释：
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此，数字总和 = 495 + 491 + 40 = 1026
 

提示：

树中节点的数目在范围 [1, 1000] 内
0 <= Node.val <= 9
树的深度不超过 10

方法DFS

void sumNumdfs(TreeNode* root, string& s, int& ans) {
	if (!root) return;
	
	s += to_string(root->val);
	sumNumdfs(root->left, s, ans);
	sumNumdfs(root->right, s, ans);
	if (!root->left && !root->right) ans += stoi(s);
	s.pop_back();
}
int sumNumbers(TreeNode* root) {
	int ans = 0; string s;
	sumNumdfs(root, s, ans);
	return ans;
}

（嵌套，n次遍历）剑指 Offer II 050. 向下的路径节点之和

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：



输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。
示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3
 

提示:

二叉树的节点个数的范围是 [0,1000]
-109 <= Node.val <= 109 
-1000 <= targetSum <= 1000 

我的方法：DFS， 20ms
思路：
root 下满足条件的路径，由以下三部分组成：
以root 为起始点的路径（往左一条，往右一条，如果节点和有0则会有很多条）+
root->left 满足条件（路径和=targetSum）的路径 +
root->right 满足条件（路径和=targetSum）的路径

注意，对于第一项 void hepPS(TreeNode* root, int targetSum, int& cnt)，这里传进去了引用int cnt，用于记录个数，不能向int helpPathSum这样直接返回结果。

void hepPS(TreeNode* root, int targetSum, int& cnt) {
	if (!root) return;
	if (targetSum == root->val) cnt++;
	hepPS(root->left, targetSum - root->val, cnt);
	hepPS(root->right, targetSum - root->val, cnt);
	return;
}
int  helpPathSum(TreeNode* root, int targetSum) {
	if (!root) return 0;
	int start = 0;
	hepPS(root, targetSum, start);
	int left = helpPathSum(root->left, targetSum);
	int right = helpPathSum(root->right, targetSum);
	return start + left + right;
}
int pathSum(TreeNode* root, int targetSum) {
	return helpPathSum(root, targetSum);
}

合并， 不建议，复杂度较高，40ms

void helpPathSum(TreeNode* root, int targetSum, int fix, bool flag, int& ans) {
	if (!root) return;
	if (targetSum == root->val) ans++;
	helpPathSum(root->left, targetSum - root->val, fix, true, ans);
	helpPathSum(root->right, targetSum - root->val, fix, true, ans);
	if (flag == false) {
		helpPathSum(root->left, fix, fix, false, ans);
		helpPathSum(root->right, fix, fix, false, ans);
	}
	return;
}
int pathSum(TreeNode* root, int targetSum) {
	int ans = 0;
	helpPathSum(root, targetSum, targetSum, false, ans);
	return ans;
}

方法二: 使用前缀和剪枝
思路与算法

我们仔细思考一下，解法一中应该存在许多重复计算。
我们定义节点的前缀和为：由根结点到当前结点的路径上所有节点的和。

我们利用先序遍历二叉树，记录下根节点 $\text{root}$ 到当前节点 $p$ 的路径上除当前节点以外所有节点的前缀和，在已保存的路径前缀和中查找是否存在前缀和刚好等于当前节点到根节点的前缀和 $curr$ 减去 $\text{targetSum}$。

对于空路径我们也需要保存预先处理一下，此时因为空路径不经过任何节点，因此它的前缀和为 $0$。

假设根节点为 $\text{root}$，我们当前刚好访问节点 $\text{node}$，则此时从根节点 $\text{root}$到节点 $\text{node}$ 的路径（无重复节点）刚好为 $\text{root}\to p_1\to p_2\to \dots \to p_k\to \text{node}$，此时我们可以已经保存了节点 $p_1,p_2,p_3,\dots ,p_k$ 的前缀和，并且计算出了节点 $\text{node}$ 的前缀和。

假设当前从根节点 $\text{root}$ 到节点 $\text{node}$ 的前缀和为 $\text{curr}$ ，则此时我们在已保存的前缀和查找是否存在前缀和刚好等于 $\text{curr}-\text{targetSum}$。假设从根节点 $\text{root}$ 到节点 $\text{node}$ 的路径中存在节点 $p_i$ 到根节点 $\text{root}$ 的前缀和为 $\text{curr}-\text{targetSum}$，则节点 $p_{i+1}$ 到 $\text{node}$ 的路径上所有节点的和一定为 $\text{targetSum}$。

我们利用深度搜索遍历树，当我们退出当前节点时，我们需要及时更新已经保存的前缀和。

    unordered_map<long long, int> prefix;

    int dfs(TreeNode *root, long long curr, int targetSum) {
        if (!root) {
            return 0;
        }

        int ret = 0;
        curr += root->val;
        if (prefix.count(curr - targetSum)) {
            ret = prefix[curr - targetSum];
        }

        prefix[curr]++;
        ret += dfs(root->left, curr, targetSum);
        ret += dfs(root->right, curr, targetSum);
        prefix[curr]--;

        return ret;
    }

    int pathSum(TreeNode* root, int targetSum) {
        prefix[0] = 1;
        return dfs(root, 0, targetSum);
    }

（后序遍历）剑指 Offer II 051. 节点之和最大的路径

路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给定一个二叉树的根节点 root ，返回其 最大路径和，即所有路径上节点值之和的最大值。

示例 1：



输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6
示例 2：



输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42
 

提示：

树中节点数目范围是 [1, 3 * 104]
-1000 <= Node.val <= 1000

明确递归返回值
dfsMPS: 返回的是，该子树的收益，如果大于0，则选择，否则，不选。并且，每次return的时候，只会选择一条子树.
维护一个全局变量ans，每个节点都会更新一次，是否选择当前节点作为连接节点，计算收益。

int dfsMPS(TreeNode* root, int& ans){
    if (!root) return 0;
    int left = max(dfsMPS(root->left, ans), 0);
    int right = max(dfsMPS(root->right, ans), 0);
    int val = left + right + root->val;
    ans = max(ans, val);
    return root->val + max(left, right); // 
}
    int maxPathSum(TreeNode* root) {
    int ans = INT_MIN;
    dfsMPS(root, ans);
    return ans;
}

复杂度分析

时间复杂度：$O(N)$，其中 $N$ 是二叉树中的节点个数。对每个节点访问不超过 $2$ 次。

空间复杂度：$O(N)$，其中 $N$ 是二叉树中的节点个数。空间复杂度主要取决于递归调用层数，最大层数等于二叉树的高度，最坏情况下，二叉树的高度等于二叉树中的节点个数。

（中序遍历）剑指 Offer II 052. 展平二叉搜索树

给你一棵二叉搜索树，请 按中序遍历 将其重新排列为一棵递增顺序搜索树，使树中最左边的节点成为树的根节点，并且每个节点没有左子节点，只有一个右子节点。

示例 1：



输入：root = [5,3,6,2,4,null,8,1,null,null,null,7,9]
输出：[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]
示例 2：



输入：root = [5,1,7]
输出：[1,null,5,null,7]
 

提示：

树中节点数的取值范围是 [1, 100]
0 <= Node.val <= 1000

我的方法：DFS，生成一颗新的树
唯一要注意的是：指针也需要引用传递

void dfsIBST(TreeNode* root, TreeNode*& tmp){
    if (!root) return;
    dfsIBST(root->left, tmp);
    tmp->right = new TreeNode(root->val);
    tmp = tmp->right;
    dfsIBST(root->right, tmp);
}
TreeNode* increasingBST(TreeNode* root) {
    TreeNode* tmp = new TreeNode(0), *ans = tmp;
    dfsIBST(root, tmp);
    return ans->right;
}

复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是二叉搜索树的节点总数。
• 空间复杂度：$O(n)$，其中 $n$ 是二叉搜索树的节点总数。需要长度为 $n$ 的列表保存二叉搜索树的所有节点的值。

（中序遍历）剑指 Offer II 053. 二叉搜索树中的中序后继

给定一棵二叉搜索树和其中的一个节点 p ，找到该节点在树中的中序后继。如果节点没有中序后继，请返回 null 。

节点 p 的后继是值比 p.val 大的节点中键值最小的节点，即按中序遍历的顺序节点 p 的下一个节点。

示例 1：



输入：root = [2,1,3], p = 1
输出：2
解释：这里 1 的中序后继是 2。请注意 p 和返回值都应是 TreeNode 类型。
示例 2：



输入：root = [5,3,6,2,4,null,null,1], p = 6
输出：null
解释：因为给出的节点没有中序后继，所以答案就返回 null 了。
 

提示：

树中节点的数目在范围 [1, 104] 内。
-105 <= Node.val <= 105
树中各节点的值均保证唯一。

我的方法：中序遍历树，将结点全部存到数组中，超级慢

void dfsIS(TreeNode* root, TreeNode*  const&p, vector<TreeNode*>& ans){
    if (!root) return;

    dfsIS(root->left, p, ans);
    ans.push_back(root);
    dfsIS(root->right, p, ans);
   return;
}
TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
    vector<TreeNode*> ans;
    dfsIS(root, p, ans);
    for (int i=0; i<ans.size(); i++){
        if (ans[i]==p && i+1<ans.size()) return ans[i+1]; 
    }
   return nullptr;
}

复杂度：O(n + vector扩容的时间), n为节点数

解法0：递归

class Solution {
public:
TreeNode* ans = nullptr;
void dfs(TreeNode* root, TreeNode*& p, TreeNode*& pre){
    if (!root) return;
    if (ans) return; // 剪枝
    dfs(root->left, p, pre);
    if (pre==p) ans = root;
    pre = root; 
    dfs(root->right, p, pre);
}
TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
    TreeNode* pre;
    dfs(root, p, pre);
    return ans;
}

解法一：中序遍历，迭代法（更快一点，不需要完全遍历树）
本题，迭代法可以直接退出循环结构，因此可考虑用迭代法。

TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
    stack<TreeNode*> stk; TreeNode* prev = nullptr;
    while (!stk.empty() || root){
        while (root){
            stk.push(root);
            root = root->left;
        }
        root = stk.top(); stk.pop();
        if (prev == p) return root;
        prev = root;
        root = root->right;
    }
    return nullptr;
}

复杂度：O(n)，主要取决于 p 在树中的位置

解法二：利用二叉搜索树的性质

TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
        TreeNode *successor = nullptr;
        if (p->right != nullptr) {
            successor = p->right;
            while (successor->left != nullptr) {
                successor = successor->left;
            }
            return successor;
        }
        TreeNode *node = root;
        while (node != nullptr) {
            if (node->val > p->val) {
                successor = node;
                node = node->left;
            } else {
                node = node->right;
            }
        }
        return successor;
    }

复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是二叉搜索树的节点数。遍历的节点数不超过二叉搜索树的高度，平均情况是 $O(\log n)$，最坏情况是 $O(n)$。
• 空间复杂度：O(1)。

（逆序遍历）剑指 Offer II 054. 所有大于等于节点的值之和

给定一个二叉搜索树，请将它的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键 小于 节点键的节点。
节点的右子树仅包含键 大于 节点键的节点。
左右子树也必须是二叉搜索树。

示例 1：



输入：root = [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2：

输入：root = [0,null,1]
输出：[1,null,1]
示例 3：

输入：root = [1,0,2]
输出：[3,3,2]
示例 4：

输入：root = [3,2,4,1]
输出：[7,9,4,10]
 

提示：

树中的节点数介于 0 和 104 之间。
每个节点的值介于 -104 和 104 之间。
树中的所有值 互不相同 。
给定的树为二叉搜索树。

迭代

    def convertBST(self, root: TreeNode) -> TreeNode:
        a, pre = [], None
        cur = root
        while(a or root):
            while root:
                a.append(root)
                root = root.right
            root = a.pop()
            if (pre==None): pre = root.val
            else: 
                root.val += pre
                pre = root.val
            root = root.left
        return cur

dfs递归

    void dfs(TreeNode* root, int& pre){
        if (!root) return;
        dfs(root->right, pre);
        root->val += pre;
        pre = root->val;
        dfs(root->left, pre);
    }
    TreeNode* convertBST(TreeNode* root) {
        int a = 0;
        dfs(root, a);
        return root;
    }

(中序遍历，py版)剑指 Offer II 055. 二叉搜索树迭代器

实现一个二叉搜索树迭代器类BSTIterator ，表示一个按中序遍历二叉搜索树（BST）的迭代器：

BSTIterator(TreeNode root) 初始化 BSTIterator 类的一个对象。BST 的根节点 root 会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字，且该数字小于 BST 中的任何元素。
boolean hasNext() 如果向指针右侧遍历存在数字，则返回 true ；否则返回 false 。
int next()将指针向右移动，然后返回指针处的数字。
注意，指针初始化为一个不存在于 BST 中的数字，所以对 next() 的首次调用将返回 BST 中的最小元素。

可以假设 next() 调用总是有效的，也就是说，当调用 next() 时，BST 的中序遍历中至少存在一个下一个数字。

示例：



输入
inputs = ["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"]
inputs = [[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
输出
[null, 3, 7, true, 9, true, 15, true, 20, false]

解释
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next();    // 返回 3
bSTIterator.next();    // 返回 7
bSTIterator.hasNext(); // 返回 True
bSTIterator.next();    // 返回 9
bSTIterator.hasNext(); // 返回 True
bSTIterator.next();    // 返回 15
bSTIterator.hasNext(); // 返回 True
bSTIterator.next();    // 返回 20
bSTIterator.hasNext(); // 返回 False
 

提示：

树中节点的数目在范围 [1, 105] 内
0 <= Node.val <= 106
最多调用 105 次 hasNext 和 next 操作

class BSTIterator:

    def __init__(self, root: TreeNode):
        self.vec = []
        self.idx = 0
        self.dfs(root)

    def dfs(self, root):
        if (not root): return
        self.dfs(root.left)
        self.vec.append(root.val)
        self.dfs(root.right)
        return

    def next(self) -> int:
        ans = self.vec[self.idx]
        self.idx += 1
        return ans

    def hasNext(self) -> bool:
        return self.idx < len(self.vec)

(遍历+哈希表 or DFS 存list + 双指针， py版) 剑指 Offer II 056. 二叉搜索树中两个节点之和

给定一个二叉搜索树的 根节点 root 和一个整数 k , 请判断该二叉搜索树中是否存在两个节点它们的值之和等于 k 。假设二叉搜索树中节点的值均唯一。

示例 1：

输入: root = [8,6,10,5,7,9,11], k = 12
输出: true
解释: 节点 5 和节点 7 之和等于 12
示例 2：

输入: root = [8,6,10,5,7,9,11], k = 22
输出: false
解释: 不存在两个节点值之和为 22 的节点
 

提示：

二叉树的节点个数的范围是  [1, 104].
-104 <= Node.val <= 104
root 为二叉搜索树
-105 <= k <= 105

我的愚蠢方法：存list，再遍历二分

class Solution:
    def __init__(self):
        self.vec = []

    def dfs(self, root:TreeNode):
        if not root: return
        self.dfs(root.left)
        self.vec.append(root.val)
        self.dfs(root.right)

    def search(self, arr:list, l:int, r:int, t:int)->bool:
        while (l < r):
            m = l + (r-l)//2
            if arr[m] == t: return True
            elif arr[m] < t:
                l = m+1
            else: r = m
        return False
    def findTarget(self, root: TreeNode, k: int) -> bool:
        self.dfs(root)
        vec = self.vec
        for i in range(len(vec)):
            if (self.search(vec, i+1, len(vec), k-vec[i])): return True
        return False

• O（nlogn）

解法二：改进：list + 双指针

初始时两个指针分别指向第一个元素位置和最后一个元素的位置。每次计算两个指针指向的两个元素之和，并和目标值比较。

• 如果两个元素之和 = 目标值，则发现了唯一解。
• 如果两个元素之和 < 目标值，则将左侧指针右移一位。
• 如果两个元素之和 > 目标值，则将右侧指针左移一位。
• 移动指针之后，重复上述操作，直到找到答案。

使用双指针的实质是缩小查找范围。那么会不会把可能的解过滤掉？答案是不会。(类似于接雨水那道题，看似贪心会漏解，实际上并不会)

假设 $\text{numbers}[i]+\text{numbers}[j]=\text{target}$ 是唯一解，其中 $0\le i<j\le \text{numbers}.\text{length}-1$。
初始时两个指针分别指向下标 $0$ 和下标 $\text{numbers}.\text{length}-1$，左指针指向的下标小于或等于 $i$，右指针指向的下标大于或等于 $j$。除非初始时左指针和右指针已经位于下标 $i$ 和 $j$，否则一定是左指针先到达下标 $i$ 的位置或者右指针先到达下标 $j$ 的位置。

• 如果左指针先到达下标 $i$ 的位置，此时右指针还在下标 $j$ 的右侧，$\text{sum}>\text{target}$，因此一定是右指针左移，左指针不可能移到 $i$ 的右侧。

• 如果右指针先到达下标 $j$ 的位置，此时左指针还在下标 $i$ 的左侧，$\text{sum}<\text{target}$，因此一定是左指针右移，右指针不可能移到 $j$ 的左侧。

由此可见，在整个移动过程中，左指针不可能移到 $i$ 的右侧，右指针不可能移到 $j$ 的左侧，因此不会把可能的解过滤掉。由于题目确保有唯一的答案，因此使用双指针一定可以找到答案。

class Solution:
    def __init__(self):
        self.vec = []

    def dfs(self, root:TreeNode):
        if not root: return
        self.dfs(root.left)
        self.vec.append(root.val)
        self.dfs(root.right)

    def findTarget(self, root: TreeNode, k: int) -> bool:
        self.dfs(root)
        vec = self.vec
        l, r = 0, len(vec)-1
        while (l<r):
            cur = vec[l] + vec[r]
            if (cur == k): return True
            elif cur < k: l += 1
            else: r -= 1
        return False

复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 为二叉搜索树的大小。我们需要遍历整棵树一次，并对得到的升序数组使用双指针遍历。

• 空间复杂度：$O(n)$，其中 $n$ 为二叉搜索树的大小。主要为升序数组的开销。

解法三：DFS + 哈希 (最优)
set() 判断是否存在元素，直接使用py:if val in self.s == cpp:set.count(val)

class Solution:
    def __init__(self):
        self.s = set()

    def dfs(self, root:TreeNode, t:int)->bool:
        if not root: return False
        if t-root.val in self.s:  return True
        self.s.add(root.val)
        return self.dfs(root.left, t) or self.dfs(root.right, t)

    def findTarget(self, root: TreeNode, k: int) -> bool:
        return self.dfs(root, k)

(unorder set + dfs) 652. 寻找重复的子树

给定一棵二叉树 root，返回所有重复的子树。

对于同一类的重复子树，你只需要返回其中任意一棵的根结点即可。

如果两棵树具有相同的结构和相同的结点值，则它们是重复的。

示例 1：



输入：root = [1,2,3,4,null,2,4,null,null,4]
输出：[[2,4],[4]]
示例 2：



输入：root = [2,1,1]
输出：[[1]]
示例 3：



输入：root = [2,2,2,3,null,3,null]
输出：[[2,3],[3]]
 

提示：

树中的结点数在[1,10^4]范围内。
-200 <= Node.val <= 200

使用哈希表，记录字符串（使用 str 去记录每个子树的结构）

class Solution:
    def findDuplicateSubtrees(self, root: Optional[TreeNode]) -> List[Optional[TreeNode]]:
        from collections import defaultdict
        dic = defaultdict(int)
        ans = []
        def dfs(node: Optional[TreeNode])->str:
            if not node:
                return ""
            s = str(node.val) + "l" + dfs(node.left) + "r" + dfs(node.right) #  使用 l，r作为标识符
            if s in dic and dic[s]==1:
                ans.append(node)
            dic[s] += 1
            return s
        dfs(root)
        return ans

(set,红黑树) 剑指 Offer II 057. 值和下标之差都在给定的范围内

给你一个整数数组 nums 和两个整数 k 和 t 。请你判断是否存在 两个不同下标 i 和 j，使得 abs(nums[i] - nums[j]) <= t ，同时又满足 abs(i - j) <= k 。

如果存在则返回 true，不存在返回 false。

示例 1：

输入：nums = [1,2,3,1], k = 3, t = 0
输出：true
示例 2：

输入：nums = [1,0,1,1], k = 1, t = 2
输出：true
示例 3：

输入：nums = [1,5,9,1,5,9], k = 2, t = 3
输出：false
 

提示：

0 <= nums.length <= 2 * 104
-231 <= nums[i] <= 231 - 1
0 <= k <= 104
0 <= t <= 231 - 1

官解：红黑树+内置二分搜索方法
思路：
遍历数组nums中的每一个元素 a，并将 a 放入set中。保证set的size<=k.
对于set中的每一个元素b，找到满足 t-a <= b <= t+a的元素，则return true

max(nums[i], INT_MIN + t) - t: 防止越界

bool containsNearbyAlmostDuplicate(vector<int>& nums, int k, int t) {
    set<int> s;
    set<int>::iterator it;
    for (int i=0; i<nums.size(); i++){
        it = s.lower_bound(max(nums[i], INT_MIN + t) - t);
        if (it!=s.end() && *it <= min(nums[i], INT_MAX -t) + t) return true;
        s.insert(nums[i]);
        if (s.size()>k) s.erase(nums[i-k]);
    }
    return false;
}

桶排序
计数排序的扩展

我们按照元素的大小进行分桶，维护一个滑动窗口内的元素对应的元素。

对于元素 $x$，其影响的区间为 $[x-t,x+t]$。于是我们可以设定桶的大小为 $t+1$。如果两个元素同属一个桶，那么这两个元素必然符合条件。如果两个元素属于相邻桶，那么我们需要校验这两个元素是否差值不超过 $t$。如果两个元素既不属于同一个桶，也不属于相邻桶，那么这两个元素必然不符合条件。

具体地，我们遍历该序列，假设当前遍历到元素 $x$ ，那么我们首先检查 $x$ 所属于的桶是否已经存在元素，如果存在，那么我们就找到了一对符合条件的元素，否则我们继续检查两个相邻的桶内是否存在符合条件的元素。

实现方面，我们将 $\text{int}$ 范围内的每一个整数 $x$ 表示为 $x=(t+1)\times a+b(0\le b\le t)$ 的形式，这样 $x$ 即归属于编号为 aa 的桶。因为一个桶内至多只会有一个元素，所以我们使用哈希表实现即可。

【非自顶向下】687. 最长同值路径

给定一个二叉树的 root ，返回 最长的路径的长度 ，这个路径中的 每个节点具有相同值 。 这条路径可以经过也可以不经过根节点。

两个节点之间的路径长度 由它们之间的边数表示。

示例 1:



输入：root = [5,4,5,1,1,5]
输出：2
示例 2:



输入：root = [1,4,5,4,4,5]
输出：2
 

提示:

树的节点数的范围是 [0, 104] 
-1000 <= Node.val <= 1000
树的深度将不超过 1000 

非自顶向下的DFS
设计一个辅助函数 dfs，调用自身求出以一个节点为根节点的左侧最长路径 left 和右侧最长路径 right，那么经过该节点的最长路径就是 left+right
接着只需要从根节点开始dfs,不断比较更新全局变量即可

int res=0;
int dfs(TreeNode *root) //以root为路径起始点的最长路径
{
    if (!root)
        return 0;
    int left=dfs(root->left);
    int right=dfs(root->right);
    res = max(res, left + right + root->val); //更新全局变量  
    return max(left, right);   //返回左右路径较长者
}

这类题型DFS注意点：
1、left, right 代表的含义要根据题目所求设置，比如最长路径、最大路径和等等
2、全局变量 $res$ 的初值设置是 $0$ 还是 INT_MIN 要看题目节点是否存在负值, 如果存在就用 INT_MIN，否则就是 $0$
3、注意两点之间路径为1，因此一个点是不能构成路径的

注意：如果最大路径和<0,意味着该路径和对总路径和做 负贡献，因此不要计入到总路径中，将它设置为0.

class Solution:
    def longestUnivaluePath(self, root: Optional[TreeNode]) -> int:
        def dfs(root: Optional[TreeNode])->int:
            if not root:
                return 0
            l, r = dfs(root.left), dfs(root.right)
            if root.left and root.val==root.left.val:
                l += 1
            else:
                l = 0
            if root.right and root.val==root.right.val:
                r += 1
            else:
                r = 0
            ans[0] = max(ans[0], l+r)
            return max(l, r)
        ans = [0]
        dfs(root)
        return ans[0]

线段树

将数组转为 二叉堆存储，每个节点存的是线段和

307. 区域和检索 - 数组可修改

给你一个数组 nums ，请你完成两类查询。

其中一类查询要求 更新 数组 nums 下标对应的值
另一类查询要求返回数组 nums 中索引 left 和索引 right 之间（ 包含 ）的 nums元素的 和 ，其中 left <= right
实现 NumArray 类：

• NumArray(int[] nums) 用整数数组 nums 初始化对象
• void update(int index, int val) 将 nums[index] 的值 更新 为 val
• int sumRange(int left, int right) 返回数组 nums 中索引 left 和索引 right 之间（ 包含 ）的nums元素的 和 （即，nums[left] + nums[left + 1], ..., nums[right]）

示例 1：

输入：
["NumArray", "sumRange", "update", "sumRange"]
[[[1, 3, 5]], [0, 2], [1, 2], [0, 2]]
输出：
[null, 9, null, 8]

解释：
NumArray numArray = new NumArray([1, 3, 5]);
numArray.sumRange(0, 2); // 返回 1 + 3 + 5 = 9
numArray.update(1, 2);   // nums = [1,2,5]
numArray.sumRange(0, 2); // 返回 1 + 2 + 5 = 8
 

提示：

1 <= nums.length <= 3 * 104
-100 <= nums[i] <= 100
0 <= index < nums.length
-100 <= val <= 100
0 <= left <= right < nums.length
调用 update 和 sumRange 方法次数不大于 3 * 10^4 

本题使用线段树的原因：

1. 对于求和querry操作来说，使用前缀和技巧能将其时间复杂度降到 查询$O(1)$，但是修改(更新)操作时间复杂度为$O(n)$
2. 对于update操作来说，原数组求和为$O(n)$，修改为$O(1)$

我们想把这两个操作的复杂度中和一下，因此设计了线段树这种结构，使得二者都为$O(log(n))$

线段树 $\text{segmentTree}$
是一个二叉树，每个结点保存数组 $\text{nums}$ 在区间 $[s,e]$ 的最小值、最大值或者总和等信息。线段树可以用树也可以用数组（堆式存储）来实现。对于数组实现，假设根结点的下标为 0，如果一个结点在数组的下标为 $\text{node}$ ，那么它的左子结点下标为 $\text{node}\times 2+1$，右子结点下标为 $\text{node}\times 2+2$。

class NumArray {
public:
	int t[100000] = { 0 };
	int n;
	void buildTree(vector<int>& nums, int node, int start, int end) {
		if (start == end) {
			t[node] = nums[start];
			return;
		}
		int lNode = node * 2 + 1, rNode = node * 2 + 2;
		int mid = start + (end - start) / 2;
		buildTree(nums, lNode, start, mid);
		buildTree(nums, rNode, mid + 1, end);
		t[node] = t[lNode] + t[rNode];
	}
	void updateHelper(int index, int val, int node, int start, int end) {
		if (start == end && start == index) {
			t[node] = val;
			return;
		}
		else if (index <= end && index >= start) {
			int lnode = node * 2 + 1;
			int rnode = node * 2 + 2;
			int mid = start + (end - start) / 2;
			updateHelper(index, val, lnode, start, mid);
			updateHelper(index, val, rnode, mid + 1, end);
			t[node] = t[lnode] + t[rnode];
		}
	}
	int sumRangeHelper(int l, int r, int node, int start, int end) {
		if (l <= start && end <= r) return t[node];
		if (end < l || start > r) return 0;
		int lnode = node * 2 + 1;
		int rnode = node * 2 + 2;
		int m = start + (end - start) / 2;
		return sumRangeHelper(l, r, lnode, start, m) + sumRangeHelper(l, r, rnode, m + 1, end);
	}
	
	NumArray(vector<int>& nums) {
		this->n = nums.size() - 1;
		buildTree(nums, 0, 0, n);
	}
	void update(int index, int val) {
		updateHelper(index, val, 0, 0, n);
	}
	int sumRange(int left, int right) {
		return sumRangeHelper(left, right, 0, 0, n);
	}
};

• 建树 $\text{buildTree}$ 函数

我们在结点 $\text{node}$ 保存数组 $\text{nums}$ 在区间 $[s,e]$ 的总和。

1. $s=e$ 时，结点 $\text{node}$ 是叶子结点，它保存的值等于 $\text{nums}[s]$。

2. $s<e$ 时，结点 $\text{node}$ 的左子结点保存区间 $[s,\lfloor \frac{s+e}{2}\rfloor ]$ 的总和，右子结点保存区间 $[\lfloor \frac{s+e}{2}\rfloor +1,e]$ 的总和，那么结点 $\text{node}$ 保存的值等于它的两个子结点保存的值之和。

假设 $\text{nums}$ 的大小为 $n$，我们规定根结点 $\text{node}=0$ 保存区间 $[0,n-1]$ 的总和，然后自下而上递归地建树。

• 单点修改 $\text{change}$ 函数

当我们要修改 $\text{nums}[\text{index}]$ 的值时，我们找到对应区间 $[\text{index},\text{index}]$ 的叶子结点，直接修改叶子结点的值为 $\text{val}$，并自下而上递归地更新父结点的值。

• 范围求和 $\text{range}$ 函数

给定区间 $[\text{left},\text{right}]$ 时，我们将区间 $[\text{left},\text{right}]$ 拆成多个结点对应的区间。

1. 如果结点 $\text{node}$ 对应的区间与 $[\text{left},\text{right}]$ 相同，可以直接返回该结点的值，即当前区间和。

2. 如果结点 $\text{node}$ 对应的区间与 $[\text{left},\text{right}]$ 不同，设左子结点对应的区间的右端点为 m，那么将区间 $[\text{left},\text{right}]$ 沿点 m 拆成两个区间，分别计算左子结点和右子结点。

我们从根结点开始递归地拆分区间 $[\text{left},\text{right}]$。

vector<int> segmentTree; // 初始化需注意
 NumArray(vector<int>& nums) : n(nums.size()), segmentTree(nums.size() * 4) {
        build(0, 0, n - 1, nums);
    }

复杂度分析

• 时间复杂度：

1. 构造函数：$O(n)$，其中 n 是数组 $\text{nums}$ 的大小。二叉树的高度不超过 $\lceil \log n\rceil +1$，那么 $\text{segmentTree}$ 的大小不超过 $2^{\lceil \log n\rceil +1}-1\le 4n$，所以 $\text{build}$ 的时间复杂度为 $O(n)$。

2. $\text{update}$函数：$O(\log n)$。因为树的高度不超过 $\lceil \log n\rceil +1$，所以涉及更新的结点数不超过 $\lceil \log n\rceil +1$。

3. $\text{sumRange}$ 函数：$O(\log n)$。每层结点最多访问四个，总共访问的结点数不超过 $4\times (\lceil \log n\rceil +1)$。

• 空间复杂度：$O(n)$。保存 $\text{segmentTree}$ 需要 O(n) 的空间。

（set 红黑树）剑指 Offer II 058. 日程表

请实现一个 MyCalendar 类来存放你的日程安排。如果要添加的时间内没有其他安排，则可以存储这个新的日程安排。

MyCalendar 有一个 book(int start, int end) 方法。它意味着在 start 到 end 时间内增加一个日程安排，注意，这里的时间是半开区间，即 [start, end), 实数 x 的范围为， start <= x < end。

当两个日程安排有一些时间上的交叉时（例如两个日程安排都在同一时间内），就会产生重复预订。

每次调用 MyCalendar.book方法时，如果可以将日程安排成功添加到日历中而不会导致重复预订，返回 true。否则，返回 false 并且不要将该日程安排添加到日历中。

请按照以下步骤调用 MyCalendar 类: MyCalendar cal = new MyCalendar(); MyCalendar.book(start, end)

示例:

输入:
["MyCalendar","book","book","book"]
[[],[10,20],[15,25],[20,30]]
输出: [null,true,false,true]
解释: 
MyCalendar myCalendar = new MyCalendar();
MyCalendar.book(10, 20); // returns true 
MyCalendar.book(15, 25); // returns false ，第二个日程安排不能添加到日历中，因为时间 15 已经被第一个日程安排预定了
MyCalendar.book(20, 30); // returns true ，第三个日程安排可以添加到日历中，因为第一个日程安排并不包含时间 20 
 

 

提示：

每个测试用例，调用 MyCalendar.book 函数最多不超过 1000次。
0 <= start < end <= 109

我的方法: set 红黑树
使用set红黑树 存一个数组，按数组的第一个元素的大小生成红黑树。

1. 当 set 为空时，直接插入数组，返回true
2. 当 set 不为空时，二分搜索set中的元素，找出第一个比 start 大的元素，该元素的位置 it 有三种情况：
   2.1 it == set.end()
   2.2 it == set.begin()
   2.3 其他情况：{分为三种，见代码}

class MyCalendar {
private:
    set<vector<int>> s;
public:
    MyCalendar() {
    }
    bool book(int start, int end) {
		if (s.empty()){
			s.insert(vector<int>{start, end});
			return true;
		}
        auto it = s.lower_bound(vector<int>{start});
        int lastFis, lastSec;
        if (it==s.end()){
            lastFis=(*(--s.end()))[0];
            lastSec = (*(--s.end()))[1];
            if (lastSec<=start) {
                s.insert(vector<int>{start, end});
                return true;
            }else return false;
        }else if (it==s.begin()){
            lastFis = (*(s.begin()))[0];
            lastSec = (*(s.begin()))[1];
            if (lastFis>= end){
                s.insert(vector<int>{start, end});
                return true;
            }else return false;
        }
        else {
            if ((*it)[0] == start){ // 当it.first == start时，必重叠
                return false;
            }else if ((*it)[0] > start){ // start 在 it.first 的前面时
                auto itPre = it;
				itPre--;
                if ((*itPre)[1] <= start && end<=(*it)[0]){ // start与end夹在两个节点之间，不重叠
                    s.insert(vector<int>{start, end});
                    return true;
                }
            }
        }
        return false;
    }
};

将 vector< int > 换成 int [] 数组，可以节约一点点空间
注意，以后要传入数组为函数参数时，多用指针int* a，少用int a[]
同时，每次更新数组时，需要用 new 更新，否则，就算将指针存入set，当指针指向改变，set里的指针也会改变。

class MyComp{
public:
	bool operator()(const int a[], const int b[]) const{ //这里可以改成 int* a
		return a[0] < b[0];
	}
};

class MyCalendar {
private:
    set<int*, MyComp> s;
public:
    MyCalendar() {
    }
    bool book(int start, int end) {
		int* tmp = new int[2]{start, end};
		if (s.empty()){
			s.insert(tmp);
			return true;
		}
        auto it = s.lower_bound(tmp);
        int lastFis, lastSec;
        if (it==s.end()){
            lastFis=(*(--s.end()))[0];
            lastSec = (*(--s.end()))[1];
            if (lastSec<=start) {
                s.insert(tmp);
                return true;
            }else return false;
        }else if (it==s.begin()){
            lastFis = (*(s.begin()))[0];
            lastSec = (*(s.begin()))[1];
            if (lastFis>= end){
                s.insert(tmp);
                return true;
            }else return false;
        }
        else {
            if ((*it)[0] == start){
                return false;
            }else if ((*it)[0] > start){
                auto itPre = it;
				itPre--;
                if ((*itPre)[1] <= start && end<=(*it)[0]){
                    s.insert(tmp);
                    return true;
                }
            }
        }
		delete[] tmp;
        return false;
    }
};

解法二：map，key存start，value存end

class MyCalendar {
public:
    map<int, int> pool;
    MyCalendar() {}
    
    bool book(int start, int end) {
        // lower_bound()返回值是一个迭代器,返回指向>=end的第一个值的位置
        map<int, int>::iterator it = pool.lower_bound(end);
        // 判断是否为第一个元素，或前一个元素的结束时间<= start
        if (it == pool.begin() || (--it)->second <= start) {
            pool[start] = end;
            return true;
        }
        return false;
    }
};

时间复杂度O(logn)，空间复杂度O(n)