Python计算巴氏距离
Python计算巴氏距离
巴氏距离简介
在统计中,巴氏距离(Bhattacharyya Distance)测量两个离散或连续概率分布的相似性。它与衡量两个统计样品或种群之间的重叠量的巴氏系数密切相关。巴氏距离和巴氏系数以20世纪30年代曾在印度统计研究所工作的一个统计学家A. Bhattacharya命名。同时,巴氏系数可以被用来确定两个样本被认为相对接近的,它是用来测量中的类分类的可分离性。



总而言之,巴氏距离在遥感机器学习分类上的作用就是,选出不同时期影响重要性更大的分类指标(指数和纹理特征),以便下一步计算。


源代码
WENAME1=['mean1','var1','hom1']
WENAME2=['mean1','var1','hom1']
WEMEAN=[5.12,1.34,0.8]
WESTD=[6.12,4.23,0.25]
def cal(Mi,Mj,Sigmai,Sigmaj):
Mi=Mi
Mj=Mj
Sigmai=Sigmai
Sigmaj=Sigmaj
d_B_i_j=0.25*(0.25*((Sigmai*Sigmai)/(Sigmaj*Sigmaj)+(Sigmaj*Sigmaj)/(Sigmai*Sigmai)+2))+0.25*(((Mi-Mj)*(Mi-Mj))/(Sigmai*Sigmai)+(Sigmaj*Sigmaj))
return d_B_i_j
LAVE={}
for i in range(len(WENAME1)):
DSUM=0.0
for j in range(len(WENAME2)):
Distance=cal(WEMEAN[i],WEMEAN[j],WESTD[i],WESTD[j])
print('{}*{}的巴氏距离:{}'.format(WENAME1[i],WENAME1[j],Distance))
DSUM=DSUM+Distance
print('{}的巴氏距离求和是:{}'.format(WENAME1[i],DSUM))
AVE=DSUM/len(WENAME1)
print('{}的巴氏距离平均值是:{}'.format(WENAME1[i],AVE))
LAVE[WENAME1[i]]=AVE
print(LAVE)
SLAVE=sorted(LAVE.items(),key=lambda d:d[1],reverse=False)
print(SLAVE)
运行结果
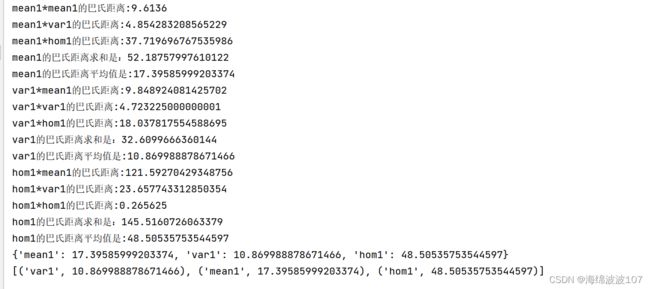
我们在代码中使用3个特征为示例,mean1,var1,hom1
并且给出了这三个特征的均值和标准差
最后程序依次计算每个指标与其他指标的巴氏距离,并用巴氏距离均值表示每个指标的平均巴氏距离,最后对这些特征进行从小到大排序,平均巴氏距离越大的特征重要性越大
代码注释
1、SLAVE=sorted(LAVE.items(),key=lambda d:d[1],reverse=False)
这段代码是对字典LAVE进行按值排序的操作。sorted()函数接受一个字典项的迭代器作为输入,并按照键或值进行排序。在这个例子中,使用lambda函数按照值(d)进行排序,并且reverse参数设置为False表示按升序排列。
使用sorted函数对字典进行排序的方法:

参考博文
- 机器学习中的数学——距离定义(二十七):巴氏距离(Bhattacharyya Distance)
- 基于光谱和纹理特征综合的农作物种植结构提取方法研究
- Python中的排序函数–sorted()函数