算法基础课第二部分
算法基础课
- 第四讲 数学知识
-
-
- AcWing1381. 阶乘(同余,因式分解)
- 质数
-
- AcWing 866. 质数的判定---试除法
- AcWing 868. 质数的判定---埃氏筛
- AcWing867. 分解质因数---试除法
- AcWing 197. 阶乘---分解质因数---埃式筛
- 约数
-
- AcWing 869. 求约数---试除法
- AcWing 870. 约数个数---试除法---质因数
- AcWing 871. 约数之和---上个题的题解
- AcWing 872. 最大公约数
- 最小公倍数
- 欧拉函数
-
- AcWing874 线性筛法求欧拉函数
- 快速幂
- 扩展欧几里得算法
- 中国剩余定理
- 高斯消元
- 求组合数
-
- AcWing885. 求组合数 I (dp)
- 201312-4csp有趣的数---组合数
- 容斥原理
- 博弈论
-
- 第五讲 动态规划
- 背包问题(有限制的选择问题)
-
- 01背包问题
-
- AcWing2. 01背包问题-max
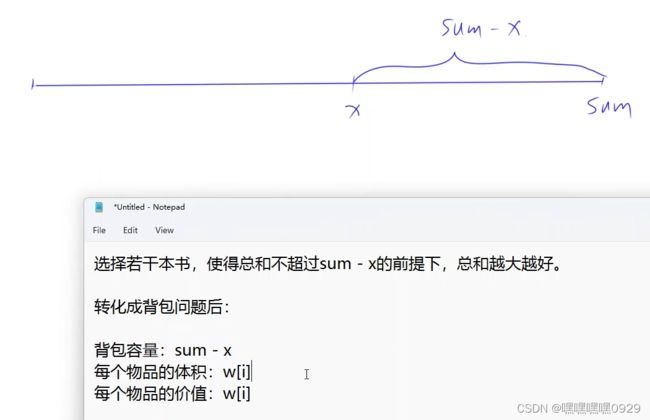
- 202209-2-csp- 何以包邮?min-》-max
- AcWing 3442. 神奇的口袋-计数
- AcWing 8. 二维费用的背包问题---二维费用
- AcWing 3417. 砝码称重
- 完全背包问题
-
- AcWing 3. 完全背包问题-max
- AcWing1371. 货币系统 -计数
- AcWing 900. 整数划分---计数
- AcWing 3382. 整数拆分-计数
- 线性DP
-
- 数字三角形模型
-
- AcWing 898. 数字三角形
- AcWing 3304. 数字三角形
- AcWing1015. 摘花生
- 最长上升子序列模型
-
- AcWing 895. 最长上升子序列(非下降子序列)
- AcWing482. 合唱队形(最长上升子序列的变形)
- 公共子序列
-
- AcWing 897. 最长公共子序列(模板题)
- 序列和
-
- AcWing 3393. 最大序列和
- AcWing 1051. 最大的和
- 区间DP
-
-
- AcWing282. 石子合并---如果是任取两堆---哈弗曼编码
- 201612-4-csp-压缩编码---与石子合并代码一样
-
- 数位统计DP
- 状态压缩DP
- 树形DP
- 记忆化搜索
- 第六讲 贪心算法
-
- 区间合并
-
- AcWing 803. 区间合并---区间左端点排序
- AcWing 422. 校门外的树---区间左端点排序
- 区间问题
-
- AcWing 905. 区间选点---区间右端点排序
- AcWing 908. 最大不相交区间数量---区间右端点排序
- AcWing 906. 区间分组---区间左端点排序
- AcWing 907. 区间覆盖---按区间左端点排序
- Huffman树
-
- AcWing 148. 合并果子
- 排序不等式
-
- AcWing 913. 排队打水
- 绝对值不等式
-
- AcWing 104. 货仓选址
- 推公式
-
- AcWing 125. 耍杂技的牛
- AcWing1055. 股票买卖 II
第四讲 数学知识
AcWing1381. 阶乘(同余,因式分解)
AcWing1381. 阶乘
#include 质数
AcWing 866. 质数的判定—试除法
AcWing 866. 试除法判定质数
#includeAcWing 868. 质数的判定—埃氏筛
埃氏筛:
筛法如何求质数捏,说起来很简单:
首先,2是公认最小的质数,所以,先把所有2的倍数去掉;
然后剩下的那些大于2的数里面,最小的是3,所以3也是质数;
然后把所有3的倍数都去掉,剩下的那些大于3的数里面,
最小的是5,所以5也是质数……
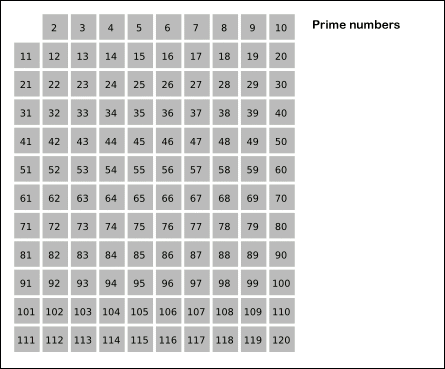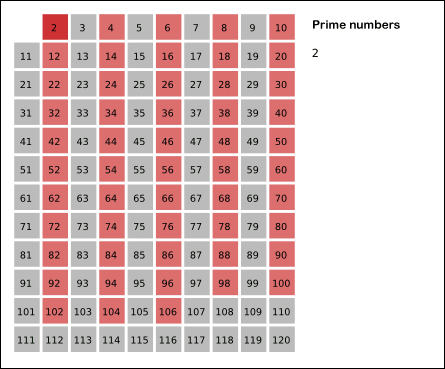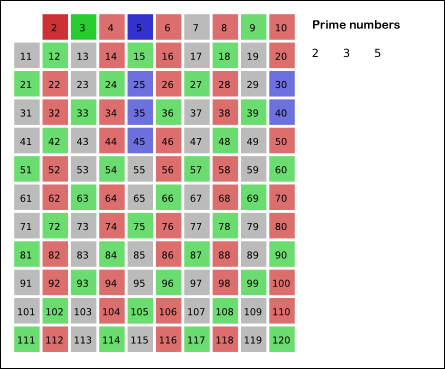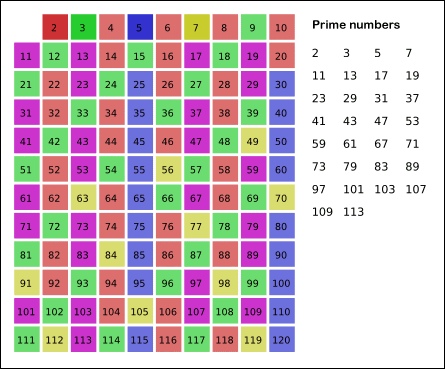
上述过程不断重复,就可以把某个范围内的合数全都除去(就像被筛子筛掉一样),剩下的就是质数了。
#includeAcWing867. 分解质因数—试除法
根据算术基本定理,不考虑排列顺序的情况下,每个正整数都能够以唯一的方式表示成它的质因数的乘积。
n=p1^a1 * p2^a2 *p3^a3.....pn^an
比如一个数16 在分解时先找到2这个质因子,然后由于16/2后还可以/2,所以会在2这个质因子上产生次方
不优化版本:从2~n 找到能整除的因子然后算次方
这里有个性质:n中最多只含有一个大于sqrt(n)的因子。
证明通过反证法:如果有两个大于sqrt(n)的因子,那么相乘会大于n,矛盾。证毕
于是我们发现最多只有一个大于sqrt(n)的因子,对其进行优化。
先考虑比sqrt(n)小的,代码和质数的判定类似最后如果n还是>1,说明这就是大于sqrt(n)的唯一质因子,输出即可。
#includeAcWing 197. 阶乘—分解质因数—埃式筛
AcWing 197. 阶乘分解
下图题解–很清晰的思路
#include约数
AcWing 869. 求约数—试除法
AcWing 869. 试除法求约数
#includeAcWing 870. 约数个数—试除法—质因数
AcWing 870. 约数个数
约数个数定理
约数之和定理–证明+实例
#includeAcWing 871. 约数之和—上个题的题解
AcWing 871. 约数之和
#includeAcWing 872. 最大公约数
AcWing 872. 最大公约数
建议直接调用c++STL中自带的__gcd()函数来求解最大公因数
(注意!函数前面有两个下划线哦。即:是“__gcd”而不是“_gcd”)
#include最小公倍数
通过最大公约数来间接计算
#include欧拉函数
AcWing874 线性筛法求欧拉函数
#include 快速幂
思路:
最后求出的幂结果实际上就是在变化过程中所有当指数为奇数时底数的乘积
3^10=3*3*3*3*3*3*3*3*3*3
//尽量想办法把指数变小来,这里的指数为10
3^10=(3*3)*(3*3)*(3*3)*(3*3)*(3*3)
3^10=(3*3)^5
3^10=9^5
//此时指数由10缩减一半变成了5,而底数变成了原来的平方,求3^10原本需要执行10次循环操作,求9^5却只需要执行5次循环操作,
但是3^10却等于9^5,我们用一次(底数做平方操作)的操作减少了原本一半的循环量,特别是在幂特别大的时候效果非常好,
例如2^10000=4^5000,底数只是做了一个小小的平方操作,而指数就从10000变成了5000,减少了5000次的循环操作。
//现在我们的问题是如何把指数5变成原来的一半,5是一个奇数,5的一半是2.5,但是我们知道,指数不能为小数,
因此我们不能这么简单粗暴的直接执行5/2,然而,这里还有另一种方法能表示9^5
9^5=(9^4)*(9^1)
//此时我们抽出了一个底数的一次方,这里即为9^1,这个9^1我们先单独移出来,剩下的9^4又能够在执行“缩指数”操作了,把指数缩小一半,底数执行平方操作
9^5=(81^2)*(9^1)
//把指数缩小一半,底数执行平方操作
9^5=(6561^1)*(9^1)
//此时,我们发现指数又变成了一个奇数1,按照上面对指数为奇数的操作方法,应该抽出了一个底数的一次方,这里即为6561^1,这个6561^1我们先单独移出来,
但是此时指数却变成了0,也就意味着我们无法再进行“缩指数”操作了。
9^5=(6561^0)*(9^1)*(6561^1)=1*(9^1)*(6561^1)=(9^1)*(6561^1)=9*6561=59049
我们能够发现,最后的结果是9*6561,而9是怎么产生的?是不是当指数为奇数5时,此时底数为9。那6561又是怎么产生的呢?是不是当指数为奇数1时,此时的底数为6561。
所以我们能发现一个规律:最后求出的幂结果实际上就是在变化过程中所有当指数为奇数时底数的乘积。
所以我们能发现一个规律:最后求出的幂结果实际上就是在变化过程中所有当指数为奇数时底数的乘积。
#include扩展欧几里得算法
中国剩余定理
高斯消元
求组合数
AcWing885. 求组合数 I (dp)
AcWing 885. 求组合数 I
#include201312-4csp有趣的数—组合数
#include容斥原理
博弈论
第五讲 动态规划
背包问题(有限制的选择问题)
01背包问题
AcWing2. 01背包问题-max
acwing2. 01背包问题
从大到小
#include一维优化
01背包问题模板:
for (int i = 1; i <= n; i ++)
for (int j = 背包容量 ; j >=容量; j --)//注意了,这里的j是从大到小枚举,和完全背包不一样(相反)
f[j] = max (f[j] , f[j - w[i]] + v[i]) ;
#include 202209-2-csp- 何以包邮?min-》-max
AcWing 4700. 何以包邮?
70分写法
#include#includeAcWing 3442. 神奇的口袋-计数
AcWing 3442. 神奇的口袋
这道题也是一道01背包问题
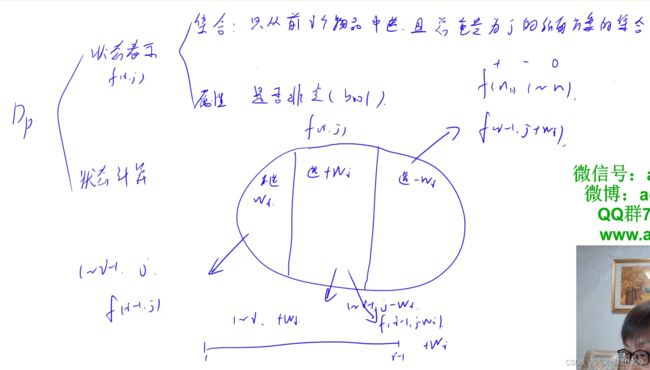
之前的f[i][j]:从前i个物品中选,且总体积不超过j的选法集合;
现在的f[i][j]:从前i个物品中选,体积正好等于j的选法的集合;
属性变化---max--->计数
这时候就与w[]无关了,那么在状态转移方程书写的时候:
表示不取第i个物品且体积正好等于j,f[i][j]=f[i - 1][j]
能够包含第i件物品时f[i][j]=f[i-1][j]+f[i-1][j-v[i]]因为表示的是不同的取法,一个包含第i个物品,一个不包含第i个物品
f数组的初始化也和01背包问题不大相同
以前是体积不超过j,且选取的物品不超过i的最大价值,当i=0的时候表示什么都没选,自然最大价值就是0,
f[0][0]=0;
现在是表示前i个物品选择之后,体积正好等于j的选法之和,f[i][0]表示什么都没选的时候,体积正好等于0,
f[i][0]=1;这是这种状态下唯一的一种选法
但是f[0][1]....f[0][40]就表示什么都不选的情况下体积等于1-40的情况,没有一种选法会是这样,因此为0
f[0][j]=0;
#include一维优化
#includeAcWing 8. 二维费用的背包问题—二维费用
#includeAcWing 3417. 砝码称重
AcWing 3417. 砝码称重
#include完全背包问题
AcWing 3. 完全背包问题-max
AcWing 3. 完全背包问题
AcWing 3. 完全背包问题—状态转移方程
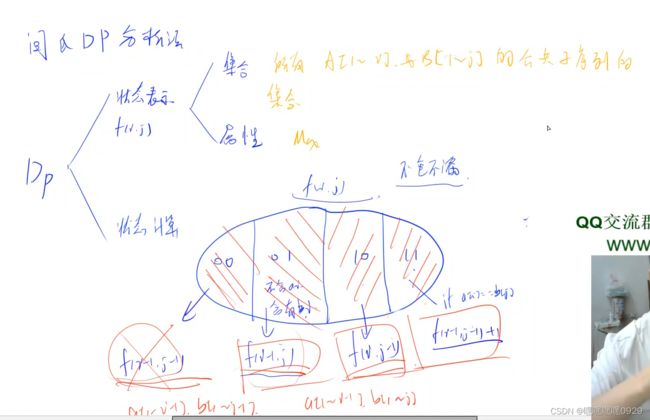
闫氏DP分析法
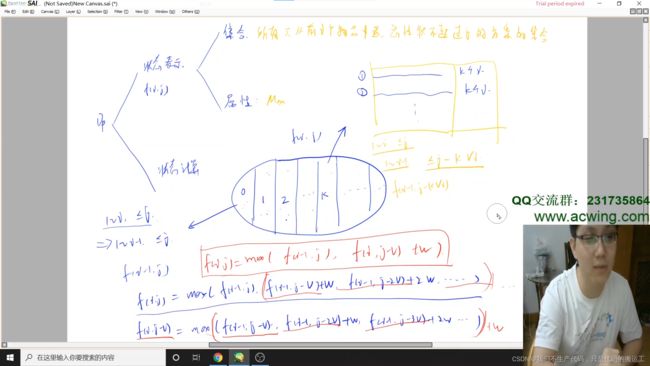
注意状态转移方程的区别
#include一维写法
完全背包问题模板:
for (int i = 1; i <= n; i ++)
for (int j = 体积; j <= 背包容量; j ++)//注意了,这里的j是从小到大枚举,和01背包不一样
f[j] = max (f[j] , f[j - w[i]] + v[i]) ;
#includeAcWing1371. 货币系统 -计数
acwing1371. 货币系统
视频讲解
最初写法(未优化)
#include一维优化
#includeAcWing 900. 整数划分—计数
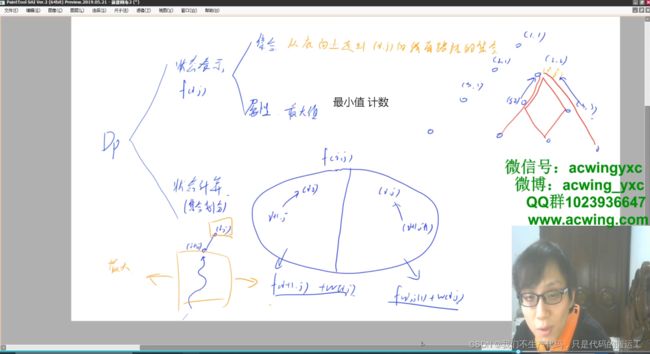
AcWing 900. 整数划分
完全背包问题模板:
for (int i = 1; i <= n; i ++)
for (int j = 体积; j <= 背包容量; j ++)
f[j] = max (f[j] , f[j - w[i]] + v[i]) ;
#includeAcWing 3382. 整数拆分-计数
AcWing 3382. 整数拆分
#include线性DP
数字三角形模型
AcWing 898. 数字三角形
AcWing 898. 数字三角形
#include从上到下
#includeAcWing 3304. 数字三角形
AcWing 3304. 数字三角形
从上到下dp
#includeAcWing1015. 摘花生
#include最长上升子序列模型
AcWing 895. 最长上升子序列(非下降子序列)
AcWing 895. 最长上升子序列
#includeAcWing482. 合唱队形(最长上升子序列的变形)
#include公共子序列
AcWing 897. 最长公共子序列(模板题)
#include序列和
AcWing 3393. 最大序列和
AcWing 3393. 最大序列和
#includeAcWing 1051. 最大的和
acwing 1051. 最大的和
本题使用一个常用技巧: 前后缀分解
该技巧的常用套路如下:
1. 求前缀数组
2. 求后缀数组
3. 枚举前后缀数组的分界点
对于本题,可以分解为求连续数组前缀和的最大值和, 求连续数组后缀和的最大值
可以定义如下:
f[i]: 从1~i从前往后枚举,以数字a[i]结尾的,连续和的最大值
g[j]: 从n~j从后往前枚举,以数字a[j]结尾的,连续和的最大值
f_max[i]: 从1~ i从前往后枚举,前1~j个数字连续和的最大值
g_max[j]: 从n~ j从后往前枚举,后n~j个数字连续和的最大值
最后枚举前后缀数组的分界点
总体时间复杂度: O(N)
#include区间DP
AcWing282. 石子合并—如果是任取两堆—哈弗曼编码
acwing282. 石子合并
AcWing 282. 石子合并(区间 DP 模版题详解分析)
#include201612-4-csp-压缩编码—与石子合并代码一样
AcWing 3240. 压缩编码
AcWing 3240. 压缩编码 哈夫曼树与区间DP的区别+绘图理解
#include数位统计DP
状态压缩DP
树形DP
记忆化搜索
第六讲 贪心算法
区间合并
AcWing 803. 区间合并—区间左端点排序
AcWing 803. 区间合并
贪心按左端点水过
思路:
就是以左端点进行排序,每次让下一个集合与该集合的右端点进行比较即可。
小心--------经典的错误,标准的零分
#includeAcWing 422. 校门外的树—区间左端点排序
AcWing 422. 校门外的树
视频讲解
朴素写法
#include pair数组写法
#include 结构体写法
#include 区间问题
AcWing 905. 区间选点—区间右端点排序
AcWing 905. 区间选点
AcWing 908. 最大不相交区间数量—区间右端点排序
AcWing 908. 最大不相交区间数量
两道题的代码完全一样
最大不相交区间数量=相交区间数量(例如:下图中的123中选择2)+不相交区间数量(例如:下图中的4)=1+1=2
#includeAcWing 906. 区间分组—区间左端点排序
#includeAcWing 907. 区间覆盖—按区间左端点排序
AcWing 907. 区间覆盖
图解:区间覆盖(按左端点排序,在左端点≤st的情况下,选择右端点最大的区间)
#includeHuffman树
AcWing 148. 合并果子
AcWing 148. 合并果子
我们可以用贪心的方法,让每次合并的两堆果子的数量都尽可能小,取当前h中的两个最小值,合并。
则每次合并消耗的体力最少,总消耗体力就最少,记录体力的同时,还要将产生的新果子堆重新插入。
既然有了取最小值与插入新堆两个操作,我们就想到了用小根堆。
#include排序不等式
AcWing 913. 排队打水
AcWing 913. 排队打水
#include绝对值不等式
AcWing 104. 货仓选址
#include推公式
AcWing 125. 耍杂技的牛
AcWing 125. 耍杂技的牛
贪心的证明
#include
int ans=-2e9;//返回最大的风险值
int sum=0;//此时某头牛头上所有牛的总重量
for(int i=0;i<n;i++)
{
q[i].first-=q[i].second;//q[i].first保存的仅为第i头牛的重量
ans=max(ans,sum-q[i].second);
sum+=q[i].first;
}
cout<<ans<<endl;//输出最大风险值的最小可能值
return 0;
}
AcWing1055. 股票买卖 II
操作分解---满足性质---各自之间互不影响
题意
输入一支股票每天的价钱,这只股票可以进行多次买入卖出,求最大利益
相关思路
当后一天大于前一天时,在前一天买入,后一天卖出,最后得到的就是最大利益
(一个跨度为多天的交易,都可以用若干个跨度等于一天的交易来计算)
acwing1055. 股票买卖 II(贪心)
#include