算法整理：外排序篇-置换选择排序&&最佳归并树

外部排序分为几个步骤，首先根据内存将待排序文件分段，然后按照分段依次将每个分段的数据读入内存排序，最后将排序后的分段通过归并算法组合在一起。在排序的过程算法对外存的读写十分耗时，所以要尽量减少外存的读写。由于每次归并都要对所有数据进行一遍外存的读写，所以减少算法归并次数就能减少外存读写次数。而减少归并次数可以从两个方面入手：1.减少初始分段数；2.增加归并路数。
在介绍 多路平衡归并时已经介绍了增加归并路数的方法，下面介绍减少初始分段数的方法。

置换-选择排序

选择-置换排序是减少初始分段数外排序算法。
由于内部排序的方法都是在内存中对数据进行排序的，所以用这些方法得到的归并段长度完全依赖于内存工作区的大小。因而置换-选择排序没有采用先读取数据再排序的方法，而是边读取边排序。

假设初始待排文件为F，第 $i$ 个分段文件为 $P_i$，内存工作区为M，工作区的可容纳m个记录，当前最小记录为MIN。则选择-置换排序的流程为：

1. 从文件F读取m个记录到内存M，令 $i=0$
2. 从M中选择最小的记录，记为MIN，并将MIN输出到 $P_i$中
3. 若F不空，从F中读取一个记录到M
4. 从所有比MIN大的数据中选择最小的数据作为新的MIN，并将其输入到 $P_i$中。
5. 重复3-4步，直到选不出MIN，此时$i$加1，
6. 重复2-5步，直到M为空。

从内存区中选择最小数据使用败者树实现，为了实现第4步，在实现败者树的过程中需要注意一下几点：

• 待排序元素有两个值，一个分段号，另一个是元素实际的值
• 从文件中读取数据后，首先要将元素的值与MIN比较，如果元素小于MIN则元素的分段号等于$i+1$，反之等于 $i$。
• 调整败者树时，需要比较两个值，先比较元素所属分段号，分段号小者胜利，如果分段号相同，比较元素值，元素值小者胜利

C++代码

//排序包含10万个整数的文件，假设内存最多可容纳10000个元素
const int BuffSize = 10000;//假设最大缓存空间为10000
int CreateLosser(vector> &list, array &LosserTree);
int AdjustLosser(vector> &list, array &LosserTree, int index);
void Replace_Selection(string filepath) {
	ifstream in(filepath);
	ofstream out;
	vector> list;
	int filenum = 0;
	string temp;
	int min = -0x3f3f3f3f;
	int winner = BuffSize;
	while (list.size() < BuffSize) {
		if (in >> temp) {
			list.push_back({ stoi(temp),filenum });
		}
		else break;
	}
	list.push_back({ min,0 });//最后一个位置放“最小值”，用于初始化败者树
	array LosserTree;
	out.open("subsection_0_" + to_string(filenum) + ".txt");
	winner = CreateLosser(list, LosserTree);
	out << to_string(list[winner].first) << endl;
	while (true)
	{
		if (in >> temp) {
			if (stoi(temp) < min) {
				list[winner] = { stoi(temp),filenum + 1 };
			}
			else {
				list[winner] = { stoi(temp),filenum };
			}
		}
		else {
			list[winner] = { 0x3f3f3f3f,filenum + 1 };
		}
		winner = AdjustLosser(list, LosserTree, winner);
		min = list[winner].first;
		if (min == 0x3f3f3f3f)break;
		if (list[winner].second > filenum) {
			out.close();
			filenum++;
			out.open("subsection_0_" + to_string(filenum) + ".txt");
			out << to_string(min) << endl;
		}
		else {
			out << to_string(min) << endl;
		}
	}
	in.close();
	out.close();
}

int CreateLosser(vector> &list, array &LosserTree) {
	for (auto &item : LosserTree)item = BuffSize;
	int winner = BuffSize;
	for (int i = 0; i < BuffSize; i++) {
		winner = AdjustLosser(list, LosserTree, i);
	}
	return winner;
}

int AdjustLosser(vector> &list, array &LosserTree,int index) {
	int winner = index;
    index = index + LosserTree.size();
	while (index>0)
	{
		index = (index - 1) / 2;
		if (list[winner].second > list[LosserTree[index]].second) {
			int temp = LosserTree[index];
			LosserTree[index] = winner;
			winner = temp;
		}
		else if (list[winner].second == list[LosserTree[index]].second) {
			if (list[winner].first > list[LosserTree[index]].first) {
				int temp = LosserTree[index];
				LosserTree[index] = winner;
				winner = temp;
			}
		}
	}
	return  winner;
}

算法分析
通过选择-置换排序得到的分段长度不等，且初始归并段的平均长度为内存工作区的两倍。也就是说如果内存工作区可以容纳m个元素，则经过排序后的得到分段的平均长度为2m。与使用内排序的方法相比，选择-置换排序产生的分段数量减少了到原来的$\frac{1}{2}$。
若不计入读入写出数据所需的时间，对于n个记录，选择-置换排序仅需$O(nlogm)$的时间复杂度就可以将所有数据排序。

最佳归并树

在介绍最佳归并树之前，首先必须要知道什么是哈夫曼树。

从树中一个结点到另一个结点之间的分支构成两个节点之间的路径，路径上的分支数目称为路径长度。而树的路径长度是从树根到每一个节点的路径长度之和。
对于带权的节点的路径长度为从该节点到树根之间的路径程度和节点上权的乘积。树的带权路径长度为书中所有叶子结点的带权路径长度之和。
带权路径长度最小的二叉树被称作哈弗曼树。

置换-选择排序生成的分段长度是不相等的，对于这个不相等的分段直接执行多路平衡归并结果不一定最好。例如，置换-选择排序生成初始分段的长度分别为：[9，30，12，18，3，17，2，6，24]，如果使用3-路归并，则其归并树如下：

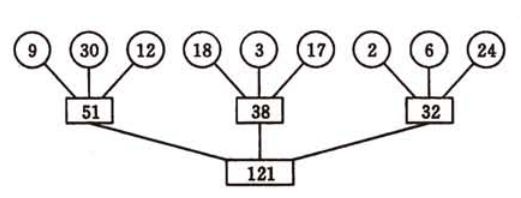
整个归并需要对外存的读写次数为484，恰好为归并树带权路径长度的两倍。这给了我们提醒，是不是减少归并树的带权路径长度，就能减少外存读写次数呢？
答案是肯定的，我们可以针对不同长短的分段，构造一颗哈弗曼树（不一定是二叉树，可以是3叉、4叉等），以减少外存的读写次数。我们称这棵哈弗曼树为最佳归并树。针对上面那个问题，构造如下所示的最佳归并树，即可将外存读写次数从484次减少到446次。

补充虚段
假如有8个初始分段，而要构造一棵三叉的最佳归并树，该怎么办呢？——补充长度为0虚段。
例如，针对如下8个分段[9，12，18，3，17，2，6，24]，构造一个三叉的最佳归并树，其结构如下，其中红色的节点为长度为0的虚段，用来辅助归并树的构建。

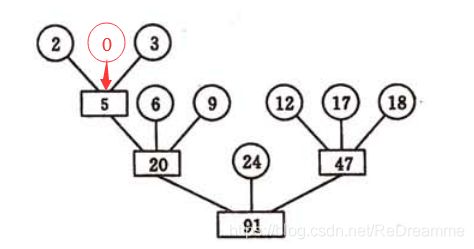
那么到底如何确定添加的虚段的数量呢?
一般的，假设分段数为 $n$，最佳归并树的路数为 $k$，若$(m-1)MOD(k-1)=0$，则不用加虚段，否则需要增加 $k-(m-1)MOD(k-1)-1$ 个虚段。(第一次归并为 $(m-1)MOD(k-1)+1$路归并 )。

C++代码（仅给出部分）

//排序包含10万个整数的文件，接置换-选择排序，置换-选择排序和败者树的实现细节不再给出
void BestMerge(list> &files) {
	int addedSegment = merge_k - (files.size() - 1) % (merge_k - 1) - 1;
	for (int i = 0; i < addedSegment; i++)files.push_back({ 0,"" });
	while (files.size()>1)
	{
		files.sort([](pair a, pairb) {return a.first < b.first; });
		Merge_K(files);
	}
}

void Merge_K(list> &files) {
	const int buffersSize = BuffSize / (merge_k + 1);

	array, merge_k> inputBuffer;
	vector outputBuffer;

	vector maxval;
	maxval.push_back(-1);
	array::iterator, merge_k + 1> inputbfIterators;
	inputbfIterators[merge_k] = maxval.begin();

	int mergenum = 0;
	string temp;

	arrayreader;
	for (int i = 0; i < merge_k; i++) {
		if (files.front().first>0) {
			reader[i].open(files.front().second);
			files.pop_front();
			for (int j = 0; j < buffersSize; j++) {
				if (reader[i] >> temp)inputBuffer[i].push_back(stoi(temp));
				else break;
			}
		}
		else {
			files.pop_front();
			inputBuffer[i].push_back(0x3f3f3f3f);
		}
		inputbfIterators[i] = inputBuffer[i].begin();
	}

	ofstream writer("subsection_filenum_" + to_string(files.size()+1) + ".txt");
	int outputnum = 0;

	array lossertree;
	int winner = CreateLosserTree(lossertree, inputbfIterators);

	while (true) {
		for (int i = 0; i < merge_k; i++) {
			if (inputbfIterators[i] == inputBuffer[i].end()) {
				
				inputBuffer[i].clear();
				for (int k = 0; k < buffersSize; k++) {
					if (reader[i] >> temp)inputBuffer[i].push_back(stoi(temp));
					else {
						inputBuffer[i].push_back(0x3f3f3f3f);
						break;
					}
				}
				inputbfIterators[i] = inputBuffer[i].begin();
			}
		}
		if (outputBuffer.size() >= buffersSize) {
			for (auto item : outputBuffer) {
				writer << to_string(item) << endl;
				outputnum++;
			}
			outputBuffer.clear();
		}
		winner = Adjust(lossertree, inputbfIterators, winner);
		if (*(inputbfIterators[winner]) != 0x3f3f3f3f)outputBuffer.push_back(*(inputbfIterators[winner]++));
		else break;
	}
	if (outputBuffer.size() > 0) {
		for (auto item : outputBuffer) {
			writer << to_string(item) << endl;
			outputnum++;
		}
	}
	files.push_back({ outputnum,"subsection_filenum_" + to_string(files.size()+1) + ".txt" });
	cout << "生成文件" << "subsection_filenum_" + to_string(files.size()) + ".txt" << endl;
	fFILENAMEilenum = files.size();
}