数据结构 外部排序（败者树、置换-选择排序、最佳归并树）

前言

我们知道，计算机在处理数据的时候会先把数据读入内存，然后做相应操作后再写回内存。例如排序，当你内存大小大于数据量的时候，排序所要考虑的时间复杂度仅仅只有在内存中的部分，我们称它为内部排序；相对地，当内存不够，数据量大时，我们就要考虑分阶段进行排序，并且还伴随着大量的 I/O 操作，我们称后者为外部排序。

本文主要讲外部排序中的败者树、置换选择排序、最佳归并树的算法原理，至于代码细节不做考虑。

---

原理

对于外部排序的顶层设计，我们大致可以归纳为三大步骤：首先，尽可能地读入数据到内存中进行内部排序，之后我们把排序完毕地数据进行写入文件操作，最后我们将这多个排序完成地段进行合并。

显然，我们对于这个排序不能使用类似直接选择排序类似的离线型算法，因为我们无法知道整体的最优点是否被当前数据段包含。所以我们采用类似归并排序的思想，对数据进行按段合并，只不过合并的时候采用 K路合并 ，也就是有 K个段。

根据上述思想，我们可以大致计算外部排序的时间：

假设 n 个记录进行外部排序的总时间为T，内部排序（初始化有序归并段 m 段）的时间为 $m\ast t_{IS}$ ，进行数据 I/O 操作 d 次的时间为 $d\ast t_{IO}$ ，进行内部归并所需时间为 $s\ast n\ast t_{mg}$，其中 s 为归并的趟数，n 为记录数。
$$T=m\ast t_{IS}+d\ast t_{IO}+s\ast n\ast t_{mg}(Ⅰ)$$

其中，对于文件在外存中存储方式是以『物理块』为单位的，也就是一次 I/O 可能读入多个记录，故我们算 d 的时候应该以记录数 n 和一块物理块的容量 c 进行相除，得到的才是一次对所有数据 I/O 的操作次数，除此之外，在初始化归并段的时候还要额外算一次 I/O 时间，所以公式如下：
$$d=2\ast \lceil \frac{n}{c}\rceil \ast (s+1)(Ⅱ)$$
对于 m 个初始段，l 为初始时分段的记录数，我们则可以大致算出它的一个上界：
$$m=\lceil \frac{n}{l}\rceil (Ⅲ)$$
对于 k 路合并，其结构可以抽象为一棵 k 叉树，则叶子节点数量为 m 。则归并树的高度为：
$$s=\lceil {\log }_{k}m\rceil (Ⅳ)$$

对于上述时间单位，$t_{IS}$ 为初始化归并段进行内部排序所需的内部排序时间，$t_{IO}$ 为物理块一次读或者写的时间，$t_{mg}$ 为内部归并的时间。显然，$t_{IO}$ 的时间取决于外部存储设备的性能，能确定的是它远大于 $t_{mg}$ ，所以我们提高外部排序的性能主要是要降低 d 的次数。

则我们可以通过降低 m 的数量或者提升 k 的路数来达到降低 d 的效果。

---

算法

多路归并平衡和败者树

对于多路归并部分的算法，由于子归并段已经有序，此时我们考虑两种算法进行合并

---

朴素合并

流程

对于当前的 m 个归并段，每次枚举其中 m 个队头的最小值，当所有队列操作结束时，合并的队列显然有序。

证明

对于每趟归并，我们需要做 $(n-1)(k-1)$ 次的比较，而 S 趟归并则需：
$$\begin{gathered} s\ast (n-1)\ast (k-1) \\ =\lceil {\log }_{k}m\rceil \ast (n-1)\ast (k-1) \\ =\lceil {\log }_{2}m\rceil \ast (n-1)\ast \frac{(k-1)}{\lceil {\log }_{2}k\rceil }(Ⅴ) \end{gathered}$$
可以发现，朴素地合并虽然能降低合并 IO 的次数，但内部归并的时间会随k的增大而递增，两者总把总时间增减相互抵消，总时间 T 基本趋于不变。

---

败者树

我们根据树形选择排序的思想可以建立一棵败者树。败者树就是对于分支节点存两个子树中的败者（对于本处败着的定义就是两个数字中较大的那个的下标索引），对于树的根节点再定义一个双亲结点，表示整个树的胜者。（对于这边就是整个树种最小的数的下标索引）

注意这边要区别于树形选择排序的竞赛树，或者也可以称位胜者树。

流程

每次从根结点的双亲结点获取到当前的最小值，然后把该叶子结点处的所在段取下一个数字，并更新从这个位置开始到达根部的所有结点。

如果该当前元素大于父节点的元素，也就是比上一轮的『败者』更劣，则上轮的败者作为该子树的胜者继续往上更新，而本元素则更新为本子树的败者也就是当前父节点的值。

对于败者树还有这样的理解：每个分支结点表示两个子树中胜者中对抗后失败的结点。类比到比赛中，相当于两个队伍从各自的分区获胜晋级上来了，对抗后赢的队伍还要继续往上晋级，而失败的队伍就结束了，对此进行颁奖表彰它到目前的成绩，也就是在当前结点记录这个败者。

证明

不难看出，败者树是一个完全二叉树，深度为 $\lceil {\log }_{2}k\rceil$，那么，在更新的时候最多要比较 $\lceil {\log }_{2}k\rceil$ 次，所以总的比较次数：
$$\begin{gathered} s\ast (n-1)\ast \lceil {\log }_{2}k\rceil \\ =\lceil {\log }_{k}m\rceil \ast (n-1)\ast \lceil {\log }_{2}k\rceil \\ =\lceil {\log }_{2}m\rceil \ast (n-1)\ast \frac{(k-1)}{\lceil {\log }_{2}k\rceil }\ast \lceil {\log }_{2}k\rceil = \\ \lceil {\log }_{2}m\rceil \ast (n-1)(Ⅵ) \end{gathered}$$
这个算法就与 k 的变化无关，故能降低总的时间复杂度。

---

置换-选择排序

本算法用于生成初始归并段，由于 $m=\lceil \frac{n}{l}\rceil$ ，所以我们要降低 m 可以提高 l 的数量，根据本算法则会把 l 的数量尽可能地提高。

思想

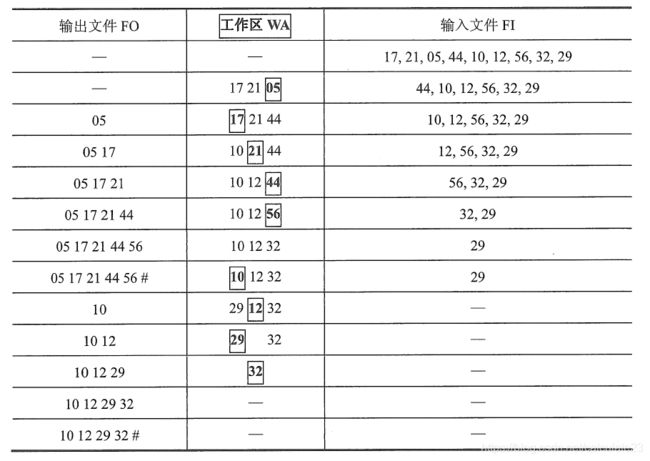
我们定义输出文件为 FO ，工作区为 WA ，输入文件为 FI ，其中工作区有 w 个元素。

起初，从输入文件按顺序输入 w 个记录到 WA 中。

接着，找到这 w 个元素中的最小值到 FO 中，为什么要最小值，因为这样才能保持有序，当然，如果 FO 中有元素，这个最小值还得大于等于 FO 中最后一次输入的元素。

之后，从 FI 再输入一个记录来替代被拿出去的位置，如果这个元素比之前输出的元素要小，显然这个记录不属于当前段，放着就好了。

最后，当工作区 WA 没元素或者没有一个比之前最后一次输出道 FO 的元素要大的，则这个归并段达到最大值了。

重复以上操作后，m 个归并段初始化完毕。

我们不难发现，实际上，上述算法是在有限的工作区操作长度尽可能地把序列划分称多个有序地段，当然这不是 m 段全局的递增子序列，因为受限于工作区 WA 的大小无法考虑到全局。

注意：不同的归并段 l 长度一般不相同，并且可以根据推雪机模型证明出 l 长度的期望为 2w 。

流程

例题

1. 设待排文件 FI = {17, 21, 05, 44, 10, 12, 56, 32, 29}，WA容量为 3 。
   

算法

对于这当中 w 个数的最小值我们可以用枚举的方法，当然，根据上一节提到的败者树我们可以结合起来，降低查询的复杂度，提升效率。

首先，我们需要尽力这 w 个记录的败者树，并且由于这 w 个记录不一定属于第一个归并段，也就是说我们操作过程中需要定义一个下限，当小于这个下限的最小值我们将它归为下一个归并段，所以我们需要对上节的败者树的逻辑稍微调整一下：多开一个字段表示元素所属的段落，在更新败者树的时候，如果新加的元素属于下一段（小于下限），那么无论如何它都属于败者，即使它比兄弟结点来得小。

---

最佳归并树

这边利用的是赫夫曼树的思想，拓展到 n 叉树中，之前的博客有提到过 传送门 。

实际上就是添加权值为 0 的虚结点使得 N 叉树最优，因为这边的归并操作的 IO 次数的计算等于归并树的带权路径和的两倍。

至于要添加的虚结点数量公式比较容易推，略。

---

End