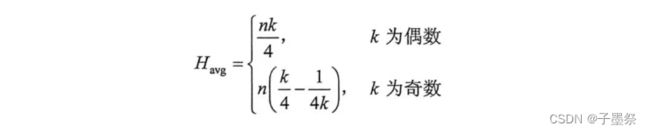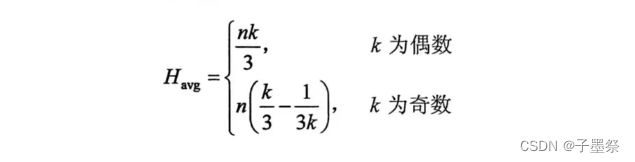片上网络(2)拓扑结构
前言
片上网络的拓扑(topology)确定了网络中节点和通道之间的物理布局和连接。拓扑对网络的整体成本效率(cost-performance) 有相当重要的影响。拓扑决定了一条消息的跳数或经过的路由器个数,以及每跳经过的互连线的物理距离,因此会对网络延迟产生显著的影响。因为信息经过路由器(router)和链路(link)需要消耗能量,所以拓扑对跳数的影响会直接反映在网络的功耗方面。此外,拓扑决定了节点之间可用路径的总数,从而影响网络扩散流量及满足带宽需求的能力。拓扑的实现复杂度取决于两个因素:每个节点上的链路数量(即节点度)和在芯片上布局拓扑的难易程度(即所需的导线长度和金属布线层数)。
总线是最简单的拓扑之一,它使用一个共享的通道来连接一组组件。总线上的所有组件都可以观察到总线上的每一条消息。因此,总线是一种有效的广播方式。然而,由于不断增加组件会造成共享通道趋近饱和,总线的可扩展性是十分受限的。
在本章中,我们将重点研究交换拓扑(switched topology)。在交换拓扑中,一组组件通过路由器和链路进行连接。我们首先描述几个指标,这些指标可以帮助我们在比较拓扑时形成一些直觉性的理解。接下来,我们将描述片上网络中常用的几个拓扑结构,并且利用之前描述的指标对它们进行比较。
一、指标
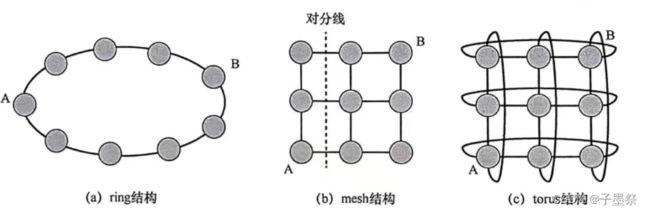
在设计片上网络时,需要首要考虑拓扑。因此,在确定片上网络的其他部分(如路由、流控制和微体系结构)之前就需要有能够快速比较不同拓扑的方法。下图展示了三种在片上网络中常用的拓扑结构(ring、mesh和 torus结构)。其中, ring 结构中的所有节点组成了一个一维的环形;在二维 mesh 结构(2D mesh)中,节点组成了规则的二维网格,每个节点与其四周的邻近节点相连;而 torus结构则是对 mesh结构的进一步改进,它通过将网络两侧边缘的对应节点相连,使网格在这一维度上构成了环路。
1.1与网络流量无关的指标
1.度(degree)
一个拓扑的度表示每个节点拥有的链路数量。 ring结构中的每个节点有两条链路,所以它的度为 2; torus 结构中的每个节点与4个相邻的节点间都存在链路,所以它的度为4。而 mesh 结构中不同位置节点的度是不同的。度是一个可以有效衡量网络开销的指标,节点的度越大,表示节点路由器需要越多的端口。相应地,路由器的实现复杂度及面积和功耗都会有所增大。我们把每个路由器的端口数称为路由器基数(router radix)。
2. 对分带宽(bisection bandwidth)
对分带宽是指将网络划分为两个相同部分后,两部分之间的通信带宽。例如,在上图中,穿过 ring结构的对分线的链路数量为2,穿过 mesh 结构的对分线的链路数量为3,穿过 torus 结构的对分线的链路数量为6。这一带宽指标可以有效地反映特定网络在最坏工作情况下的性能,因为对分带宽限制了可以从系统一端移动到另一端的总数据量。另外,这一指标同时也表示了实现片上网络时所必需的全局连线数量,所以它也可以用来衡量网络的开销。相对于评价片外网络而言,对分带宽其实并不能很好地评价片上网络,因为片上的全局连线资源同芯片与片外通信的引脚带宽资源相比,连线资源要丰富得多。
3.网络直径(diameter)
网络直径指的是拓扑中任意两个节点之间的最短路径组成的集合中的最大值(即网络中所有源-目的节点对的最短路径中的跳数最大值)。例如,ring 和 mesh 结构的网络直径为4, torus结构的网络直径为2。在没有链路竞争的情况下,网络直径可以作为衡量拓扑中最大延迟的指标。
1.2与网络流量相关的指标
1. 跳数(hop count)
从一个节点路由至下一个节点称为一跳(hop)。跳数是指一条消息从源节点路由到目的节点需要跳的总次数,或者指这条消息所通过的链路总数。这是一个可以简单有效地反映网络延迟的指标,因为即使在网络内部没有竞争的情况下,网络中的每一个节点和链路还是会引入传输延迟的。网络的最大跳数取决于其直径。除了最大跳数,平均跳数也可以很好地反映网络延迟,其表示网络所有可能的源-目的节点对之间的路径的跳数的平均值。
当三种拓扑(ring、mesh 和 torus)具有相同数量的节点,且网络流量随机且均匀时(每一个节点向其余节点发送消息的概率均相同时), ring结构的跳数比 mesh 结构和 torus结构都要多。例如,假设所有链路均为双向链路,并且采用最短路径路由法,ring 和 mesh 结构的最大跳数都是 4,而 torus 结构的跳数为 2。torus结构的平均跳数依旧最小,为1¹/₃; mesh结构的平均跳数稍大,为1⁷/₉; ring结构的平均跳数是这三种拓扑之中最大的,为2 2\9。
2. 最大通道负载(maximum channel load)
这一指标可用于估计网络所能支持的最大带宽,或者每个节点在网络饱和前每秒可注入的最大比特数。最大通道负载与最大注入带宽(maximum injectionbandwidth)之间存在如下关系。
最大注入带宽=1/最大通道负载
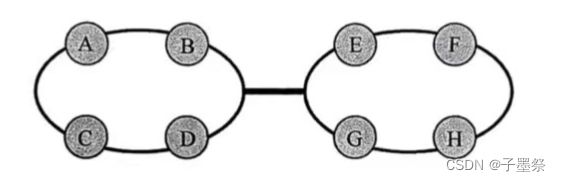
直观上,想要估计网络能够支持的最大带宽,首先需要确定在特定流量模式下网络中哪个链路最拥挤。要计算最大通道负载,首先要确定瓶颈通道。如下图,瓶颈通道就是连接两个ring结构的通道。
我们假设它为一个双向链路。在理想路由方法下,每个节点注入流量的一半将保持在其所在的 ring 结构内,而另一半将通过瓶颈通道到达另外一个 ring 结构中的节点。例如,对于由节点A 输出的每个数据包,它有 1/8 的概率到达节点B、C、D、E、F、G、H 或它本身。当数据包的目的地为节点 A、B、C、D时,数据包不经过瓶颈通道;但当它的目的地为节点E、F、G、H时,它就必须通过瓶颈通道。所以,节点A 注入带宽的1/2 将会通过瓶颈通道,对于其余节点也是如此。因此,这个瓶颈通道的负载为2。相应地,节点的最大注入带宽为1/2。结果是,网络在节点注入带宽达到 1/2时,整个网络就会饱和。向两个 ring 结构中添大更多的节点将进一步增大通道负载,从而减小网络带宽。
3. 路径多样性(path diversity)
在给定源节点和目的节点的前提下,如果这个节点对在某个拓扑中拥有多条最短路径, 而在另一个拓扑中只有一条最短路径,则认为前者的拓扑具有更大的路径多样性。拓扑中的路径多样性使路由算法在处理负载均衡问题时具有更大的灵活性,从而通过减小通道负载,提高了网络吞吐量。路径多样性还使得数据包能够拥有绕过网络中故障的潜力。图中的 ring结构没有提供路径多样性,因为在节点对之间永远只有唯一一条最短路径。
如上图(a)所示,如果一个数据包在节点A 和B之间沿顺时针方向移动,它将经过4跳;如果数据包沿逆时针方向移动,它要经过5跳。网络想要更多的传输路径,最简单的办法就是绕远。如果一个 ring 结构中节点个数为偶数,那么位于 ring结构两侧的节点由于有两个最短路径的存在,路径多样性就是2。图(b)和(c)中的 mesh 和 torus结构则提供了源-目的节点对之间更多最短路径以供选择。在图(b)的mesh 结构中,节点A 和B之间提供6条不同的最短路径,所有路径的距离都是4跳。
二、直连拓扑: ring、mesh 和 torus
直连拓扑指每个终端节点(如单芯片多处理器中的一个处理器核或缓存)都配备一个路由器的网络拓扑;所有路由器既是流量的产生与汇入端,又是流量的中转站。到目前为止,大多数片上网络的设计都使用了直连网络,因为将路由器与终端节点放在一起考虑,通常适合芯片这种存在电路面积限制的环境。
直连拓扑可以描述为 k-ary n-cube, 其中k是每个维度上的节点数,n是维度数。举个例子,4×4的mesh 或torus结构可以描述为 4-ary 2-cube,它们的维度数都是 2,每个维度上的节点数是 4,一共有 4×4=16个节点; 8×8 的 mesh或torus结构有64个节点,可以描述为 8-ar y 2-cube。同理,一个4×4×4 的mesh或torus结构有64个节点,可以描述为 4-ar y 3-cube。这样的描述方法假设每个维度上都具有相同数量的节点,所以网络的节点总数可以表示为 k”。从实际角度讲,绝大多数片上网络使用2D mesh 拓扑,以方便在平面基板上进行电路映射,因为更复杂的网络拓扑需要更多的金属布线层。这与部署在片外的网络是不同的,因为片外基板的连接线不受平面的限制,可以是立体的。在每个维度上,k个节点通过通道连接到离它们最近的邻居节点。ring 结构由于可以描述为k-ary1-cube, 所以也可以将其归为 torus类结构。
对一个 torus结构来说,所有的节点都有同样的节点度;但是,对 mesh 结构来说,网络边缘节点的度比网络中心节点的度要小。torus 结构是边缘对称的(mesh结构不是), 这个属性可以帮助 torus结构更好地平衡各通道的流量。相应地,由于不具备边缘对称性, mesh 结构对位于网络中心通道的负载要求比边缘通道高。
torus 网络在每个维度上需要两个通道,整个 torus网络需要2n个通道。因此,对一个2D torus网络来说,它的度是 4;对一个3D torus 网络来说,它的度是6。对mesh 网络来说,它的度也是和 torus网络相同的,尽管在网络边缘的端口可能不会被使用到。torus 网络的平均最小跳数是通过计算网络中所有可能的节点对之间的最短路径的均值得到的。torus 网络的平均最小跳数计算如下。
torus 网络去除环绕的链路后就是 mesh 网络。mesh 网络的平均最小跳数比torus 网络稍大, 其平均最小跳数计算如下。
对于均匀随机流量下参数k为偶数的 torus网络,其对分切割后两部分之间的最大通道负载是 k/8,其将网络最大注入带宽限制在了 8/k flit/node/cycle。对 mesh 来说,最大通道负载将会增大到k/4,因此网络最大注入带宽减小至 4/kflit/node/cycle。
和 ring网络相比, mesh 和 torus网络都具有路径多样性。随着网络维度的增加,其路径多样性也会增加。
三、非直连拓扑:交叉开关、蝶形网络、clos 网络和 fat tree 网络
非直连拓打指所有终端节点通过一个或多个中间交换节点(switch node)相连的网络拓扑。与直连拓扑中每个节点既是终端节点又是交换节点不同,直连拓扑中终端节点与交换节点是彼此分离的。只有终端节点是流量的源(发出新的流量)或目的地(处理输入的流量而不向下继续传递),中间交换节点只是流量的中转站(将流量从输入送到指定的输出)。
3.1交叉开关
最简单的非直连拓扑是交叉开关(crossbar),一个交叉开关通过 n×m个简单的交换节点连接了n个输入和m个输出。其中,n个输入和m个输出进行全连接,每个输入都连接到所有的 m个输出。这种结构是非阻塞的,因为它总是可以将发送方与特定的接收方直接连起来。
3.2蝶形网络
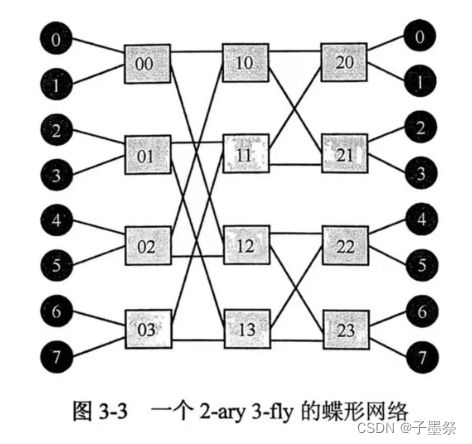
蝶形(butterfly)网络是非直连拓扑的典型例子,可以描述为 k-ary n-fly。该网络具有k²个如处理器核或内存的终端节点;该网络共有 n级交换节点,每级含kⁿ⁻¹个k×k的交换节点。换句话说, k是交换节点的入度/出度, n是交换节点的级数。下图展示了一个 2-ary 3-fly 的蝶形网络。圆形节点为终端节点,方形节点为交换节点。
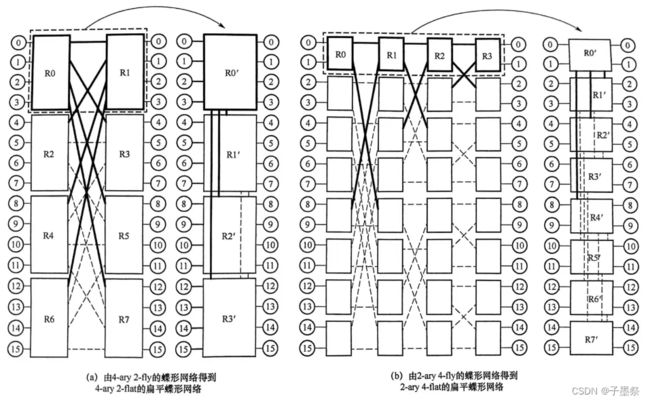
扁平蝶形网络的详细变化方法如下:
3.3 fat tree网络
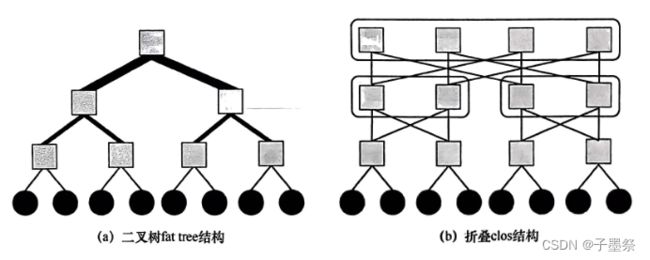
fat tree 在逻辑上是一个二叉树结构,如下图所示。一个fat tree网络可以由clos网络折叠而成。
3.4不规则拓扑
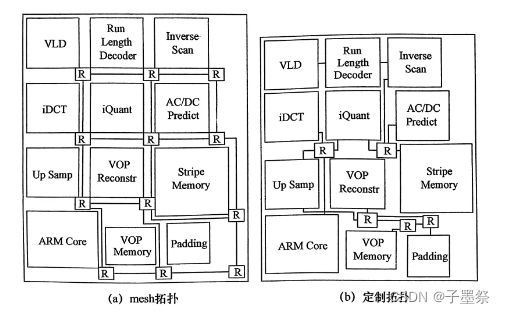
多处理器片上系统设计可以使用多种异构IP模块,可以根据具体情况,减少拓扑中交换节点和链路的数量,可以明显减小功耗和面积。
定制的拓扑对网络的连通性有一定的限制。
注:ARM的CMN-700使用的是mesh网络。