PyTorch: tensor操作(一) contiguous

tensor在内存中的存储

信息区和存储区

tensor在内存中的存储包含信息区和存储区

• 信息区（Tensor）包含tensor的形状size，步长stride，数据类型type等
• 存储区（Storage）包含存储的数据

高维数组在内存中是按照行优先顺序存储的，什么是行优先顺序？假设我们有一个(3, 4)的tensor，他其实是按照一维数组的方式存储的，只不过在tensor的信息区记录了他的size和stride导致实际上展示出的数组是二维的，size为(3, 4)

二维数组

内存中的一维形式

接下来我们看一个例子，例子表明tensor中的元素在内存上是连续的，并且也证明了确实是行优先顺序存储

tensor = torch.tensor([[[1 ,2, 3, 4], [5, 6, 7, 8], [9, 10,11,12]], 
                       [[13,14,15,16],[17,18,19,20],[21,22,23,24]]])
print(tensor.is_contiguous())
for i in range(2):
    for j in range(3):
        for k in range(4):
            print(tensor[i][j][k].data_ptr(), end=' ')
'''
True
140430616343104 140430616343112 140430616343120 140430616343128
140430616343136 140430616343144 140430616343152 140430616343160 
140430616343168 140430616343176 140430616343184 140430616343192 
140430616343200 140430616343208 140430616343216 140430616343224 
140430616343232 140430616343240 140430616343248 140430616343256 
140430616343264 140430616343272 140430616343280 140430616343288 
'''

shape && stride

继续上述的例子我们来看一下在信息区的shape和stride属性，对于(2, 3, 4)维的tensor他的shape为(2, 3 ,4)，stride为(12, 4, 1)

shape

shape很容易理解，就是tensor的维度，上述例子为(2, 3, 4)的tensor，维度就为(2, 3, 4)

stride

stride代表着多维索引的步长，每一步都代表内存上的偏移量+1，对于(2, 3, 4)维度的tensor：stride+1代表着(dim2)+1，stride+4代表其余dim不变，(dim1)+1，stride+12代表其余dim不变，(dim0)+1，如下图所示

图示stride

stride计算方法

$$strid{e}_i=strid{e}_{i+1}\ast siz{e}_{i+1}i\in [0,n-2]$$

对于shape(2, 3, 4)的tensor，计算如下(stride3=1)

$$\begin{gathered} strid{e}_2=strid{e}_3\ast shap{e}_3=1\ast 4=4 \\ strid{e}_1=strid{e}_2\ast shap{e}_2=4\ast 3=12 \end{gathered}$$

stride = [1] # 初始化第一个元素  
# 从后往前遍历迭代生成 stride  
for i in range(len(tensor.size())-2, -1, -1):  
    stride.insert(0, stride[0] * tensor.shape[i+1])  
print(stride)          # [12, 4, 1]
print(tensor.stride()) # (12, 4, 1)

理解了tensor在内存中的存储之后，我们再来看contiguous

contiguous

contiguous

返回一个连续内存的tensor

Returns a contiguous in memory tensor containing the same data as self tensor. If self tensor is already in the specified memory format, this function returns the self tensor.

什么时候用contiguous呢？

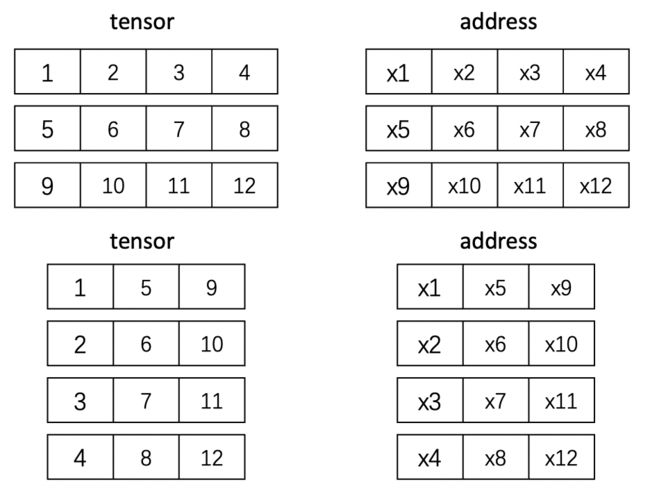
简单理解就是tensor在内存地址中的存储顺序与实际的一维索引顺序不一致时使用，如下所示，对上面的tensor进行一维索引，结果为[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]，对原tensor运用transpose进行转置，在对其进行一维索引，结果为[1, 5, 9, 2, 6, 10, 3, 7, 11, 4, 8, 12]，这时索引顺序发生了变化，所以需要用contiguous

注意：不论怎么变化每个元素对应的地址是不变的，比如11对应的地址为x11，transpose之后11依然对应x11，那么变化的是什么呢？还记得tensor分为信息区和存储区吗，存储区是不变化的，变化的是信息区的shape，stride等信息，有时间以后做介绍~

代码示例

tensor = torch.tensor([[1,2,3,4],[5,6,7,8],[9,10,11,12]])
print(tensor)
print(tensor.is_contiguous())
tensor = tensor.transpose(1, 0)
print(tensor)
print(tensor.is_contiguous())
'''
tensor([[ 1,  2,  3,  4],
        [ 5,  6,  7,  8],
        [ 9, 10, 11, 12]])
True
tensor([[ 1,  5,  9],
        [ 2,  6, 10],
        [ 3,  7, 11],
        [ 4,  8, 12]])
False
'''

为什么要用contiguous

有人可能会有疑问，既然上述情况索引与之前不一样了（不连续了），为什么要让他变连续呢？因为pytorch的某些操作需要索引和内存连续，比如view

代码示例（接着上面的例子）

tensor = tensor.contiguous()
print(tensor.is_contiguous())
tensor = tensor.view(3, 4)
print(tensor)
'''
True
tensor([[ 1,  5,  9,  2],
        [ 6, 10,  3,  7],
        [11,  4,  8, 12]])
'''

如果不用contiguous会报以下错误

RuntimeError: view size is not compatible with input tensor's size and stride (at least one dimension spans across two contiguous subspaces). Use .reshape(...) instead.

为什么contiguous能有效？

contiguous用了一种简单粗暴的方法，既然你之前的索引和内存不连续了，那我就重新开辟一块连续的内存给他加上索引即可

代码示例，从下面代码中stride变化可以看出，transpose之后的tensor确实是改变了信息区的信息

tensor = torch.tensor([[1,2,3,4],[5,6,7,8],[9,10,11,12]])
print(tensor.is_contiguous())	# True
for i in range(3):
    for j in range(4):
        print(tensor[i][j], tensor[i][j].data_ptr(), end=' ')
    print()
print(tensor.stride()) 			# (4, 1)
'''
True
tensor(1) 140430616321664 tensor(2) 140430616321672 tensor(3) 140430616321680 tensor(4) 140430616321688 
tensor(5) 140430616321696 tensor(6) 140430616321704 tensor(7) 140430616321712 tensor(8) 140430616321720 
tensor(9) 140430616321728 tensor(10) 140430616321736 tensor(11) 140430616321744 tensor(12) 140430616321752 
(4, 1)
'''

tensor = tensor.transpose(1, 0)
print(tensor.is_contiguous())	# False
for i in range(4):
    for j in range(3):
        print(tensor[i][j], tensor[i][j].data_ptr(), end=' ')
    print()
print(tensor.stride()) 			# (1, 4) changed
'''
False
tensor(1) 140430616321664 tensor(5) 140430616321696 tensor(9) 140430616321728 
tensor(2) 140430616321672 tensor(6) 140430616321704 tensor(10) 140430616321736 
tensor(3) 140430616321680 tensor(7) 140430616321712 tensor(11) 140430616321744 
tensor(4) 140430616321688 tensor(8) 140430616321720 tensor(12) 140430616321752 
(1, 4)
'''

tensor = tensor.contiguous()
print(tensor.is_contiguous())	# True
for i in range(4):
    for j in range(3):
        print(tensor[i][j], tensor[i][j].data_ptr(), end=' ')
    print()
print(tensor.stride())      	# (3, 1)
'''
True
tensor(1) 140431681244608 tensor(5) 140431681244616 tensor(9) 140431681244624 
tensor(2) 140431681244632 tensor(6) 140431681244640 tensor(10) 140431681244648 
tensor(3) 140431681244656 tensor(7) 140431681244664 tensor(11) 140431681244672 
tensor(4) 140431681244680 tensor(8) 140431681244688 tensor(12) 140431681244696 
(3, 1)
'''