C++哈希函数_哈希表_哈希冲突_负载因子_仿函数_针对字符串的模板特化特化_闭散列(线性探测)哈希表_开散列哈希桶的模拟实现(Key_Value模型数组)
文章目录
-
- 1.哈希中的基本概念
- 哈希函数
- 常见的哈希函数与缺陷
- 哈希表
- 2.哈希冲突
- 哈希冲突的解决方法(闭散列与开散列)
- 闭散列(开放地址法)
- 负载因子
- C++实现除留余数法闭散列线性探测哈希表(Key_Value模型)
- 开散列(哈希桶/拉链法)
- C++实现除留余数法开散列哈希桶(Key_Value模型)
- 3.代码位置
1.哈希中的基本概念
哈希函数
之前的二叉搜索树与红黑树以及顺序结构他们的关键字和它的储存位置没有对应关系,所以在查找一个元素时要经过多次的关键字比较。
顺序查找时间复杂度为O(N),平衡树中为树的高度,即O(logN ),搜索的效率取决于搜索过程中元素的比较次数。
如果构造一种存储结构,通过某种函数(hashFunc)使元素的存储位置与它的关键码之间能够建立一一映射的关系,那么在查找时通过该函数可以不经过任何比较,一次直接从表中得到要搜索的元素。
向该结构中插入数据时
根据待插入元素的关键字,以哈希函数计算出该元素的存储位置并按此位置进行存放
向该结构搜索数据时
利用哈希函数对元素的关键字进行同样的计算,把求得的函数值当做元素的存储位置,在结构中按此位置取元素比较,若关键字相等则搜索成功
常见的哈希函数与缺陷
常见的哈希函数有:
- 直接定址法
- 除留余数法
缺陷:
直接定址法:1.如果数据范围很大,直接定址法会浪费很多空间。
2.不能处理浮点数和字符串等数据
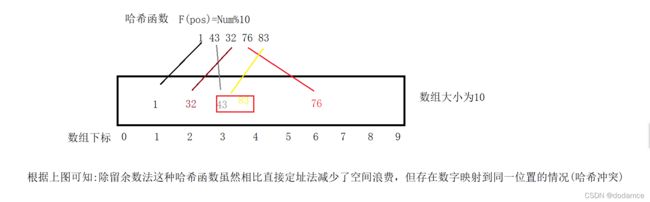
除留余数法:
哈希表
上述过程就是哈希方法,在哈希方法中使用的将关键字与数据储存建立起联系的函数为哈希函数,构造出的数组称为哈希表
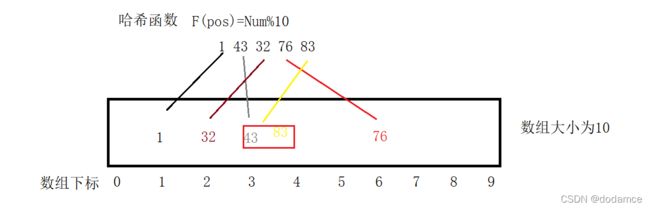
2.哈希冲突
哈希冲突的解决方法(闭散列与开散列)
闭散列(开放地址法)
闭散列解决哈希冲突有两种方法
- 线性探测法
- 二次探测法
线性探测法:
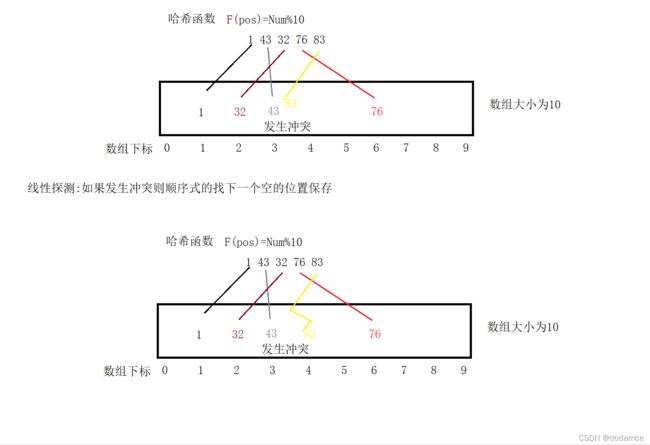
查找的时候先按照哈希函数计算映射位置。如果不是这个数字,还要依次向下一个位置继续查找。
注意: 当线性探测数组没有空位时,要对数组进行增容
线性探测的缺陷
线性探测会导致”踩踏效应“,某个位置出现冲突时,可能导致其他数据冲突
二次探测:
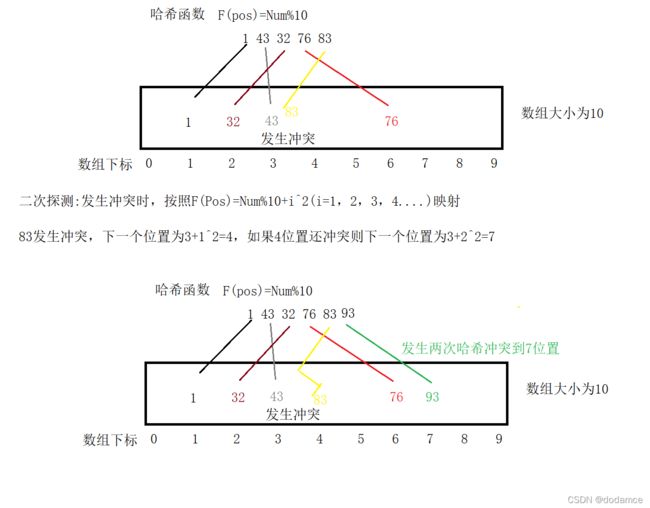
如果超过了数组大小则类似循环队列一样,又回到了数组前面。
二次探测相比于线性探测减少了踩踏现象
负载因子
负载因子=已经储存的数据个数/空间大小。
负载因子越大,冲突的概率越大,增删查改的效率越低,空间利用率低。反之
在闭散列中负载因子最大为1
在闭散列中负载因子一般设置为0.7.也就是数据占了空间的70%就要增容,否则哈希冲突太多,效率收到影响
C++实现除留余数法闭散列线性探测哈希表(Key_Value模型)
注意:
1.为了方便删除数组中的数据和标记位置为空,选择添加状态枚举标记每个元素的状态,删除某个元素即把这歌元素的状态设置为删除即可。这个位置为空就将这个位置的状态设置为空状态
2.针对字符串类型无法进行整形运算,这里选择添加仿函数,用户可以自己定义类型转化为关键字的方法
3.因为实现哈希表选择C++STL中的vector和pair实现,所以不需要写析构函数,系统会自动调用vector和pair的析构函数
Hash_Table.h
#pragma once
#includeTest_Hash_Table.cpp
#include"Hash_Table.h"
void Test()//测试插入/删除/查找/打印接口
{
CloseHash::HashTable<int, int>Table;
vector<int>ret = { 1,2,100,20,4,44 };
Table.Erase(10);
for (const auto s : ret)
{
Table.Insert(make_pair(s, s));
}
Table.PrintHashTable();
for (size_t i = 0; i < ret.size(); i++)
{
if (Table.Find(ret[i]))
{
Table.Erase(ret[i]);
Table.PrintHashTable();
}
}
}
//针对字符串类型
//方法一:自定义仿函数
//方法二:偏特化默认仿函数
//struct StrHashKey
//{
// int operator()(const string& Str)
// {
// int Sum = 0;
// for (int i = 0; i < Str.size(); i++)
// {
// Sum += Str[i];
// }
// return Sum;
// }
//};
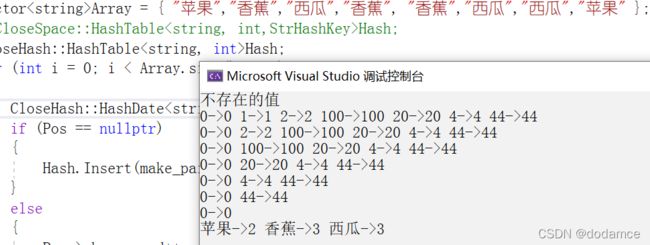
void Test2()//测试字符串类型
{
//统计次数
vector<string>Array = { "苹果","香蕉","西瓜","香蕉", "香蕉","西瓜","西瓜","苹果" };
//CloseSpace::HashTableHash;
CloseHash::HashTable<string, int>Hash;
for (int i = 0; i < Array.size(); i++)
{
CloseHash::HashDate<string,int>*Pos=Hash.Find(Array[i]);
if (Pos == nullptr)
{
Hash.Insert(make_pair(Array[i], 1));
}
else
{
Pos->_kv.second++;
}
}
Hash.PrintHashTable();
}
int main()
{
Test();
Test2();
return 0;
}
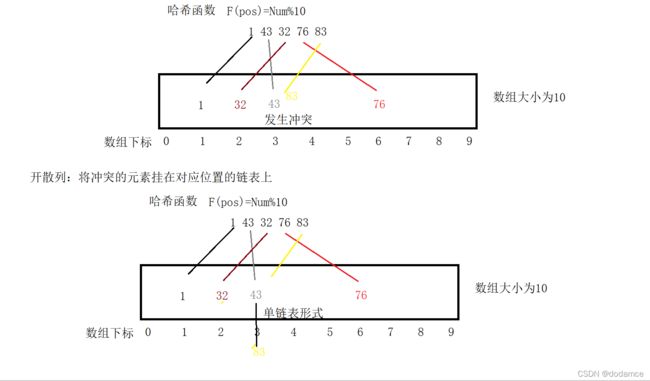
开散列(哈希桶/拉链法)
首先对关键字集合用散列函数计算散列地址,具有相同地址的关键字归于同一子集合,每一个子集合称为一个桶,各个桶中的元素通过一个单链表链接起来,各链表的头结点存储在哈希表中。
开散列一般负载因子为1时增容。相比于闭散列来讲,有效的避免了哈希冲突的踩踏现象,同时空间利用率高
C++实现除留余数法开散列哈希桶(Key_Value模型)
注意:
1.与闭散列注意点相同,要用状态标记数据的状态
2.针对字符串类型还要进行模板特化处理
3.开散列增容时不选择闭散列那样的定义新的对象复用函数。因为开散列每个位置是链表,如果在定义新对象意味着开辟新的链表节点,如果复用之前的函数就会出现释放之前旧节点,创建新节点的性能损失。
所以在开散列扩容选择:开辟新数组重新计算映射关系然后移动旧节点到新数组,最后交换数组的方法
4.HashDate中有自定义的元素指针,所以默认的析构函数不能使用,拷贝构造以及赋值运算符重载会导致浅拷贝问题
OpenHashTable.h
#pragma once
#includeOpenHashTable.cpp
#include"OpenHashTable.h"
void Test1()//测试插入/查找/删除/打印接口
{
OpenHash::Hash<int, int>Table;
vector<int>ret = { 1,2,100,20,4,44 };
for (int i = 0; i < ret.size(); i++)
{
Table.Insert(make_pair(ret[i], i));
}
Table.PrintHashTable();
for (const auto& e : ret)
{
if (Table.Find(e))
{
Table.Erase(e);
Table.PrintHashTable();
}
}
}
void Test2()//测试字符串类型
{
//统计次数
vector<string>Array = { "苹果","香蕉","西瓜","香蕉", "香蕉","西瓜","西瓜","苹果" };
OpenHash::Hash<string, int>Hash;
for (int i = 0; i < Array.size(); i++)
{
OpenHash::HashDate<string, int>* Pos = Hash.Find(Array[i]);
if (Pos == nullptr)
{
Hash.Insert(make_pair(Array[i], 1));
}
else
{
Pos->_kv.second++;
}
}
OpenHash::Hash<string, int>Copy(Hash);
OpenHash::Hash<string, int>Copy2 = Copy;
Hash.PrintHashTable();
Copy.PrintHashTable();
Copy2.PrintHashTable();
}
int main()
{
//Test1();
Test2();
return 0;
}
注意:极端情况下当所有的数据都冲突的时候,此时查找的时间复杂度为O(N)于顺序表相同。为了解决这种情况,可以将每个桶的结构由单链表的形式改成红黑树或AVL树提高查找效率
3.代码位置
Github代码位置
Gitee代码位置