ACM-数据结构-并查集

ACM竞赛中，并查集（DisjointSets）这个数据结构经常使用。顾名思义，并查集即表示集合，并且支持快速查找、合并操作。

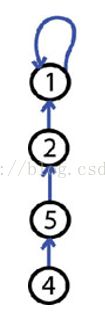
并查集如何表示一个集合？它借助树的思想，将一个集合看成一棵有根树。那又如何表示一棵树？初始状态下，一个元素即一棵树，根即是元素本身。

并查集如何支持合并操作？不难发现，按照树的思想，在同一棵树中的所有元素，根都是相同的。也就是说，合并两个不同的集合，只需要将其中一个集合的根设置为另一个集合的根即可，而需要改变根的那个集合，其实只需要改变根节点的父节点即可。

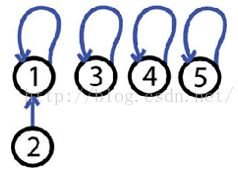
并查集如何支持快速查找操作？如果完全按照上面的合并方法进行合并操作，最后生成的树，可能是完全线性的，那么查询的时间复杂度就退化成了O(n)，因为在这种情况下，程序不得不遍历完所有节点才能查询到当前元素所属的根节点。

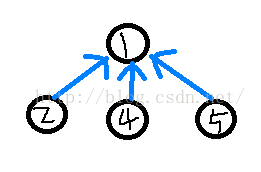
路径压缩算法优化并查集查询操作。按照集合原来的定义，集合中的元素是满足无序性的，因此可以在查询操作进行的过程中，当程序遍历到根节点然后返回的时候，将所有属于当前根节点的元素的父节点直接设置为当前根节点。如此一来，原来的一条链就变成了一般的树了。当下一次查询的时候，就可以很快的遍历到根节点了，复杂度下降为O(1)。

还有一种优化查询速度的方法，那就是合并两个集合的时候，按秩进行合并，这里的秩代表的以当前元素为根节点的元素个数。很明显，将秩较小的树合并到秩较大的树上更优。

最后，就是具体如何用代码实现并查集？其实，并查集中只涉及到了保存当前元素的父节点这一信息，所以利用一个数组set[i]代表节点i的父节点即可，如果set[i]=i那么代表当前集合的根即为i元素本身。

以一道例题为例，HDOJ：1212，时空转移（点击打开链接）：

How Many Tables

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 17478    Accepted Submission(s): 8574

Problem Description

Today is Ignatius' birthday. He invites a lot of friends. Now it's dinner time. Ignatius wants to know how many tables he needs at least. You have to notice that not all the friends know each other, and all the friends do not want to stay with strangers.

One important rule for this problem is that if I tell you A knows B, and B knows C, that means A, B, C know each other, so they can stay in one table.

For example: If I tell you A knows B, B knows C, and D knows E, so A, B, C can stay in one table, and D, E have to stay in the other one. So Ignatius needs 2 tables at least.

 

Input

The input starts with an integer T(1<=T<=25) which indicate the number of test cases. Then T test cases follow. Each test case starts with two integers N and M(1<=N,M<=1000). N indicates the number of friends, the friends are marked from 1 to N. Then M lines follow. Each line consists of two integers A and B(A!=B), that means friend A and friend B know each other. There will be a blank line between two cases.

 

Output

For each test case, just output how many tables Ignatius needs at least. Do NOT print any blanks.

 

Sample Input

  
  
    
    
    
    

     
     
     
     
   
   2
5 3
1 2
2 3
4 5

5 1
2 5
  
  
    
    
    
    

 

Sample Output

  
  
    
    
    
    

     
     
     
     
   
   2
4
  
  
    
    
    
    

 

Author

Ignatius.L

 

Source

杭电ACM省赛集训队选拔赛之热身赛

 

Recommend

Eddy   |   We have carefully selected several similar problems for you:   1325  1198  1863  1102  1162 

 

题意：

给出一些人之间关系，如果两个人有直接或间接关系，那么这两个人就属于同一个集合，最后统计集合的个数。

分析：

并查集思想，初始每一个人属于各自一个集合，如果当前读入的两个有关系的人不在同一集合，那么就合并他们所属的集合，集合个数减一。

源代码：

#include 

const int NumSets = 1005;
typedef int DisjSet[NumSets + 1];
typedef int Rank[NumSets + 1];
DisjSet S;
Rank R;

// Initialize the set and rank
void Initialize()
{
    for(int i=0; i= R[fa2])
    {
        S[fa2] = fa1;
        R[fa1] += R[fa2];
    }
    else
    {
        S[fa1] = fa2;
        R[fa2] += R[fa1];
    }
}

int main()
{//freopen("sample.txt", "r", stdin);
    int cas;
    scanf("%d", &cas);
    while(cas--)
    {
        int n, m;
        Initialize();
        scanf("%d%d", &n, &m);
        for(int i=0; i

其它并查集题目还有，HDOJ：1232、1558、1811、1829、1198。UESTC：203、1070。