数据结构——并查集
并查集是一种数据结构,是树的一种应用,用于处理一些不交集(一系列没有重复元素的集合)的合并以及查询问题。并查集支持如下操作:
- 查询:查询某个元素属于哪个集合,通常是返回集合内的一个“代表元素”。这个操作一般是为了判断两个元素是否在同一个集合之中。
- 合并:将两个集合合并为一个。
- 添加:添加一个新集合,其中有一个新元素。不如查询和合并操作重要。
我们来看下面一个比较有趣的并查集应用的例子:
话说江湖上散落着各式各样的大侠,有上千个之多。他们没有什么正当职业,整天背着剑在外面走来走去,碰到和自己不是一路人的,就免不了要打一架。但大侠们有一个优点就是讲义气,绝对不打自己的朋友。而且他们信奉“朋友的朋友就是我的朋友”,只要是能通过朋友关系串联起来的,不管拐了多少个弯,都认为是自己人。这样一来,江湖上就形成了一个一个的群落,通过两两之间的朋友关系串联起来。而不在同一个群落的人,无论如何都无法通过朋友关系连起来,于是就可以放心往死了打。但是两个原本互不相识的人,如何判断是否属于一个朋友圈呢?
我们可以在每个朋友圈内推举出一个比较有名望的人,作为该圈子的代表人物,这样,每个圈子就可以这样命名“齐达内朋友之队”“罗纳尔多朋友之队”……两人只要互相对一下自己的队长是不是同一个人,就可以确定敌友关系了。如此一来,门派便产生了。
在上面的例子中,我们可以认为每个门派都是一个集合,门派的掌门人作为集合的“代表元素”,通过确认双方的掌门人是否是同一个人来确定对方是否是自己人。对于没有门派的大侠,我们也可以认为他自己组成一个门派,掌门人就是他自己。集合的合并就类似于门派的合并,门派合并后需要重新推出一个掌门人,也就是要重新选取集合的“代表元素”。
实现方法一
实现方法一总是记住一个集合中编号最小的元素,类似一个门派中的大侠总是记住自己的掌门人是谁。
- 我们定义一个数组set[1…n],其中set[i]表示元素i所在集合;
- 用编号最小的元素标记所在集合。
我们来看下面一个例子,假设有以下不相交集合:
{1, 3, 7}, {4}, {2, 5, 9 10}, {6, 8}
数组set[1…n]为:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| set[i] | 1 | 2 | 1 | 4 | 2 | 6 | 1 | 6 | 2 | 2 |
其中1, 3, 7组成一个集合,他们中间最小为1,因此set[1]、set[3]、set[7]都为1。
假设我们现在要将{1, 3, 7}、{2, 5, 9 10}这两个集合合并,合并方式如下:
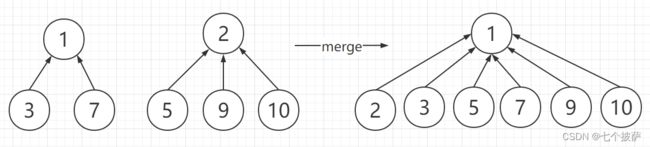
数组set[1…n]更新为:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| set[i] | 1 | 1 | 1 | 4 | 1 | 6 | 1 | 6 | 1 | 1 |
代码实现
初始化
初始时我们传入元素个数,并将set[i]设置为自身。
private int[] set;
/**
* 构造方法,初始化set数组
*
* @param num 元素数量
*/
public MergeFindSet1(int num) {
set = new int[num];
for (int i = 0; i < num; i++) {
// 初始时初始化为自身
set[i] = i;
}
}
查找方法
查找方法比较简单,由于set中记录的永远是集合当中的代表元素,因此只需要返回set[i]即可:
/**
* 查询某个元素属于哪个集合
*
* @param num
* @return
*/
public int find(int num) {
return set[num];
}
合并方法
在并查集的合并方法中,我们传入两个元素的编号,代表这两个元素在同一个集合当中。我们先找到两个元素所在集合的代表元素,接着找两个代表元素中编号大的那个,将编号大的元素的set[max]赋值为编号小代表元素min。同时由于方法一总是记住的是集合当中编号最小的,因此还需要更新set[i]=max的所有元素。
/**
* 集合的合并操作
*
* @param a
* @param b
*/
public void merge(int a, int b) {
int findA = find(a);
int findB = find(b);
int max = Math.max(findA, findB);
int min = Math.min(findA, findB);
// 用编号小的元素标记所在集合
// 同时还需要把以前同一个集合中的元素的set[i]更新
for (int i = 0; i < set.length; i++) {
if (set[i] == max) {
set[i] = min;
}
}
}
测试
public static void main(String[] args){
MergeFindSet1 mergeFindSet1 = new MergeFindSet1(11);
mergeFindSet1.merge(1, 3);
mergeFindSet1.merge(3, 7);
mergeFindSet1.merge(2, 5);
mergeFindSet1.merge(5, 9);
mergeFindSet1.merge(9, 10);
mergeFindSet1.merge(6, 8);
for (int i = 0; i < 11; i++) {
System.out.print(mergeFindSet1.find(i) + " ");
}
System.out.println("\n==={1, 3, 7}和{2, 5, 9 10}合并后===");
mergeFindSet1.merge(3, 9);
for (int i = 0; i < 11; i++) {
System.out.print(mergeFindSet1.find(i) + " ");
}
}
得到的输出结果为:
0 1 2 1 4 2 6 1 6 2 2
==={1, 3, 7}和{2, 5, 9 10}合并后===
0 1 1 1 4 1 6 1 6 1 1
和我们上面的推论一致。
实现方法二
在实现方法一中,合并方法需要搜索全部的元素,时间复杂度为O(n),效率并不是很高。
我们可以使用树结构去改造并查集的结构,对于集合中的元素,只需要记住它的上级节点。类似以下这种结构:
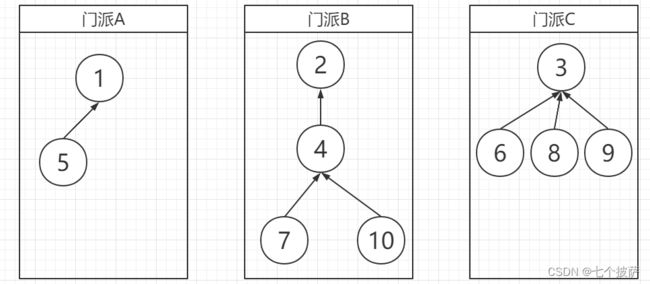
定义数组set[1…n]:
set[i]=i,则i表示本集合,并是集合对应树的根。以门派为例子,i是门派的掌门人。set[i]=j, j!=i,则j是i的父节点,以门派为例,j是i的上级。
我们以上面的例子去构造set数组,set数组为:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| set[i] | 1 | 2 | 3 | 2 | 1 | 3 | 4 | 3 | 3 | 4 |
假设我们现在需要将上图的门派A和门派B进行合并,合并后的门派A+B如下:
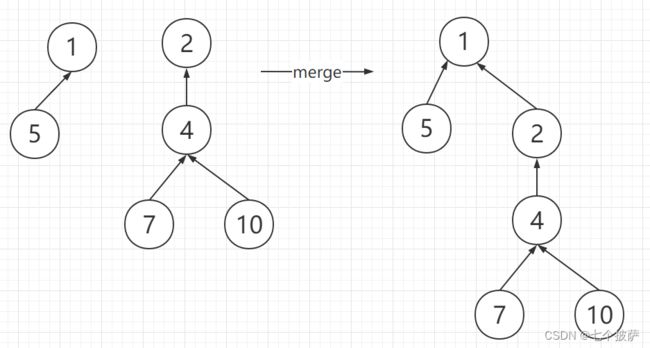
set数组更新为:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| set[i] | 1 | 1 | 3 | 2 | 1 | 3 | 4 | 3 | 3 | 4 |
代码实现
初始化
和上面方法1一样,初始化set数组,初始时set[i]都赋值为自身。
private int[] set;
public MergeFindSet2(int num) {
set = new int[num];
for (int i = 0; i < num; i++) {
// 初始时初始化为自身
set[i] = i;
}
}
查找方法
方法二查找元素所属集合就是树中的查找根节点的方式。
public int find(int num) {
while (set[num] != num) {
num = set[num];
}
return num;
}
合并方法
使用方法二进行集合合并时,以门派为例,只需要把其中一个掌门的掌门人信息更新即可。
public void merge(int a, int b) {
int findA = find(a);
int findB = find(b);
if (findA > findB) {
set[findA] = findB;
} else {
set[findB] = findA;
}
}
测试
public static void main(String[] args) {
MergeFindSet2 mergeFindSet2 = new MergeFindSet2(11);
mergeFindSet2.merge(1, 5);
mergeFindSet2.merge(4, 7);
mergeFindSet2.merge(4, 10);
mergeFindSet2.merge(2, 4);
mergeFindSet2.merge(3, 6);
mergeFindSet2.merge(3, 8);
mergeFindSet2.merge(3, 9);
for (int i : mergeFindSet2.set) {
System.out.print(i + " ");
}
System.out.println();
for (int i = 0; i < 11; i++) {
System.out.print(mergeFindSet2.find(i) + " ");
}
System.out.println("\n===========合并帮派A和B后=========");
mergeFindSet2.merge(5, 7);
for (int i : mergeFindSet2.set) {
System.out.print(i + " ");
}
System.out.println();
for (int i = 0; i < 11; i++) {
System.out.print(mergeFindSet2.find(i) + " ");
}
}
得到的输出结果为:
0 1 2 3 2 1 3 4 3 3 4
0 1 2 3 2 1 3 2 3 3 2
===========合并帮派A和B后=========
0 1 1 3 2 1 3 4 3 3 4
0 1 1 3 1 1 3 1 3 3 1
其中第一行和第四为set数组,和我们上面的推论相同。
合并方法优化
方法二在合并的时候平均时间复杂度为O(logn),相比方法一得到了改善。但是如果树为单支树,查找的时间复杂度会退化为O(n),依然存在效率问题。
方法三对merge方法进行了优化,在进行merge前会先获取两棵树的高度,merge时将高度小的树合并到高度大的树,在一定程度上维持了平衡,避免了单支树的情况。以帮派的例子为例,假如帮派A的掌门人是a,帮派B的掌门人是b,如果帮派A和帮派B要握手言和,合并为一个帮派,那么只需要让掌门a认掌门b为上级,或者让掌门b认掌门a为上级即可。那究竟是掌门a上位还是掌门b上位呢?那就要看哪个帮派的成员结构更复杂,形成的树更高了。
合并方法如下:
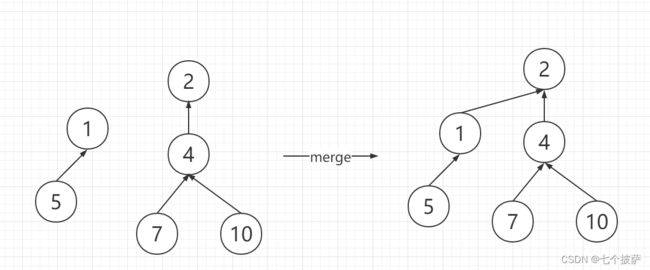
假设两棵树的高度分别为h1和h2,则合并后树的高度是:
- h1 != h2:max(h1, h2)
- h1 == h2:h1 + 1
代码实现
初始化
对比前两种方法,方法三需要增加一个height数组用于存储树的高度,height[i]表示以i为根节点的树的高度。
int[] set;
int[] height;
public MergeFindSet3(int num) {
set = new int[num];
height = new int[num];
for (int i = 0; i < num; i++) {
// 初始时初始化为自身
set[i] = i;
// 高度初始化为1
height[i] = 1;
}
}
合并方法和查询方法
这里查询方法和方法二的一样,在merge之前会先判断元素所在树的高度,根据树的高度决定如何挂树。
public void merge(int a, int b) {
int aRoot = find(a);
int bRoot = find(b);
// 两棵树高度相等时,随便挑一个作为根节点就行
if (height[aRoot] == height[bRoot]) {
set[bRoot] = aRoot;
height[aRoot] = height[aRoot] + 1;
}
// 如果a所在子树的高度比b的高,把b挂到a,a的高度不变
else if (height[aRoot] > height[bRoot]) {
set[bRoot] = aRoot;
}
// b所在子树高度比a高,把a挂到b
else {
set[aRoot] = bRoot;
}
}
public int find(int num) {
while (set[num] != num) {
num = set[num];
}
return num;
}
测试
public static void main(String[] args) {
MergeFindSet3 mergeFindSet3 = new MergeFindSet3(11);
mergeFindSet3.merge(1, 5);
mergeFindSet3.merge(2, 4);
mergeFindSet3.merge(4, 7);
mergeFindSet3.merge(4, 10);
mergeFindSet3.merge(3, 6);
mergeFindSet3.merge(3, 8);
mergeFindSet3.merge(3, 9);
System.out.print("index: ");
for (int i = 0; i < 11; i++) {
System.out.print(i + " ");
}
System.out.println();
System.out.print(" set: ");
for (int i : mergeFindSet3.set) {
System.out.print(i + " ");
}
System.out.println();
System.out.print(" root: ");
for (int i = 0; i < 11; i++) {
System.out.print(mergeFindSet3.find(i) + " ");
}
System.out.println("\n合并5和7所在集合后:");
mergeFindSet3.merge(5, 7);
System.out.print(" set: ");
for (int i : mergeFindSet3.set) {
System.out.print(i + " ");
}
System.out.println();
System.out.print(" root: ");
for (int i = 0; i < 11; i++) {
System.out.print(mergeFindSet3.find(i) + " ");
}
}
得到的输出结果为:
index: 0 1 2 3 4 5 6 7 8 9 10
set: 0 1 2 3 2 1 3 2 3 3 2
root: 0 1 2 3 2 1 3 2 3 3 2
合并5和7所在集合后:
set: 0 1 1 3 2 1 3 2 3 3 2
root: 0 1 1 3 1 1 3 1 3 3 1
路径压缩算法
路径压缩算法是对find方法的优化。考虑这样的场景,门派的结构非常复杂,门派中的每个大侠又都只知道自己的上级是谁,并不知道自己的掌门是谁,当两个大侠碰面时,他们需要一级一级向上询问来确定掌门人,这样的查找效率就比较低下。最理想的结构是所有人都知道掌门人是谁,这样就产生了路径压缩算法。当大侠找到自己的掌门是谁后,就记住自己的掌门,下次直接找掌门再确认就好。
以下图左边的树为例,假如我们要查找元素5和元素7的根节点,压缩后的路径如下:
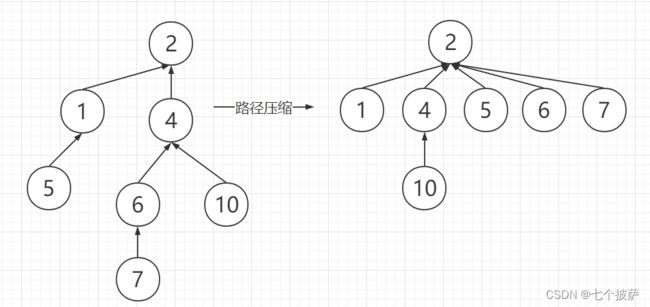
代码实现
路径压缩算法实现的find方法
public int find2(int num) {
// 查找根节点
int root = num;
while (set[root] != root) {
root = set[root];
}
// 将路径上经过的元素都指向根节点
while (set[num] != root) {
int parent = set[num];
set[num] = root;
num = parent;
}
return root;
}
测试
我们以下图为例测试方法的正确性:
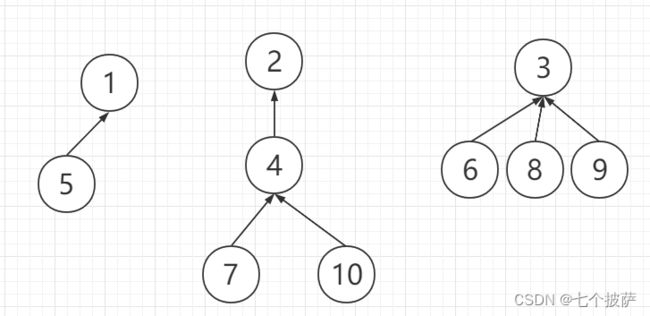
如果路径正确压缩,最终的树结构为:
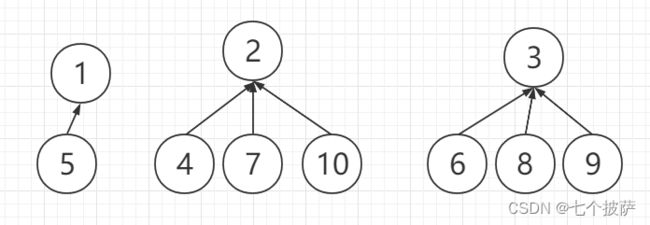
public static void main(String[] args) {
MergeFindSet2 mergeFindSet2 = new MergeFindSet2(11);
mergeFindSet2.merge(1, 5);
mergeFindSet2.merge(2, 4);
mergeFindSet2.merge(4, 7);
mergeFindSet2.merge(4, 10);
mergeFindSet2.merge(3, 6);
mergeFindSet2.merge(3, 8);
mergeFindSet2.merge(3, 9);
System.out.println("===========初始时的set数组=========");
for (int i : mergeFindSet2.set) {
System.out.print(i + " ");
}
for (int i = 0; i < 11; i++) {
mergeFindSet2.find2(i);
}
System.out.println("\n===========find一轮后的set数组=========");
for (int i : mergeFindSet2.set) {
System.out.print(i + " ");
}
}
得到的输出结果为:
===========初始时的set数组=========
0 1 2 3 2 1 3 4 3 3 4
===========find一轮后的set数组=========
0 1 2 3 2 1 3 2 3 3 2