博弈类Dp习题集

1.Problem - C - Codeforces

        （一）题目大意

                给定你一串数字，Alice和Bob玩游戏，如果Alice最后选完所有数字和为偶数，则Alice赢，否则Bob赢，现在问你谁一定会赢。

                

        （二）解题思路

                这题一看就知道是一个博弈类Dp，我们不用关心数字大小，只需要关心Alice最后拿了几个奇数，对于Alice来说它每一步棋要尽可能的使他的奇数个数为偶数，Bob来说则是要让Alice拿到奇数，对于Alice来说，他要从每一次拿奇数或者拿偶数挑一个最大的成为当前局面的最佳，而Bob则是要挑一个最小的局面让Alice输，于是我们可以用记忆化写。

                对于f[odd][player][x][y]表示当前奇数个数为odd，玩家为player，剩余奇数个数为x，剩余偶数个数为y，Dp状态定义好了，考虑边界，很容易想到，当无数可取的时候就是游戏结束的时候，输赢判断，若当前odd为奇数则返回0，否则返回1。

        （三）代码实现

#include "bits/stdc++.h"
using namespace std;
const int N = 1e2 + 10;
int f[2][2][N][N];
int dp(int odd,int player,int x,int y)
{
    if(f[odd][player][x][y] != -1) return f[odd][player][x][y];
    if(x == 0 && y == 0) return !odd;
    int cost = 0;
    if(player == 0) {
        if(x > 0) cost = max(cost,dp(odd ^ 1,player ^ 1,x - 1,y));
        if(y > 0) cost = max(cost,dp(odd,player ^ 1,x,y - 1));
    }
    else {
        cost = 1;
        if(x > 0) cost = min(cost,dp(odd,player ^ 1,x - 1,y));
        if(y > 0) cost = min(cost,dp(odd,player ^ 1,x,y - 1)); 
    }
    return f[odd][player][x][y] = cost;
}
void solve()
{
    int n,odd,eve,x;
    odd = eve = 0;
    cin >> n;
    for(int i = 1;i <= n;i++) {
        cin >> x;
        if(x & 1) odd ++;
        else eve ++;
    }
    if(dp(0,0,odd,eve)) cout << "Alice" << endl;
    else cout << "Bob" << endl;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    memset(f,-1,sizeof(f));
    int T;
    cin >> T;
    while(T --) {
        solve();
    }
    return 0;
}

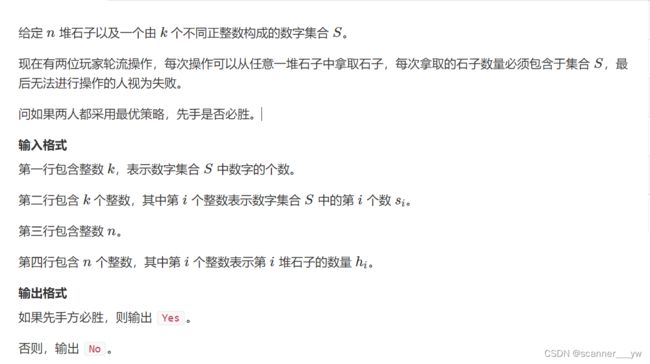
2.893. 集合-Nim游戏 - AcWing题库

        (一）题目大意

         （二）解题思路

                对于每一个操作数，我们都能得到一个NIM游戏，因此我们把这些能得到的NIM游戏的游戏值异或起来，若为0，则先手必败，否则，先手必胜。对于每一堆石头，他能操作的前提是他能够拿走一点，因此对于每一个石头我们也可以看做一个游戏，用最小补集作为游戏的值，若为0则表示不能操作了（表示必败），否则表示你能够操作使得别人达到必败态的局面（表示必胜）。

          （三）代码实现

#include "bits/stdc++.h"
using namespace std;
const int N = 10010;
int f[N],a[N],b[N];
int n,k;
int sg(int x)
{
    if(f[x] != -1) return f[x];
    set  st;
    for(int i = 1;i <= n;i++) 
        if(x >= a[i])
            st.insert(sg(x - a[i]));
    int mex = 0;
    while(st.count(mex)) mex ++;
    return f[x] = mex;
}
int main()
{
    memset(f,-1,sizeof(f));
    cin >> n;
    for(int i = 1;i <= n;i++) cin >> a[i];
    cin >> k;
    int ans = 0;
    for(int i = 1;i <= k;i++) {
        cin >> b[i];
        ans ^= sg(b[i]);
    }
    if(ans) cout << "Yes" << endl;
    else cout << "No" << endl;
    return 0;
}

3.894. 拆分-Nim游戏 - AcWing题库

        （一）题目大意

         （二）解题思路

                跟上一题解题思路类似，只不过这里对于每一堆石子，又可以拆分成两个游戏，因此我们需要枚举每一堆式子的拆分的游戏，然后把异或值放入集合中，然后算出最小补集作为这个游戏的最终值。

        （三）代码实现

#include "bits/stdc++.h"
using namespace std;
const int N = 110;
int f[N];
int sg(int x)
{
    if(f[x] != -1) return f[x];
    set  st;
    for(int i = 0;i < x;i++)
        for(int j = 0;j <= i;j++)
            st.insert(sg(i) ^ sg(j));
    int mex = 0;
    while(st.count(mex)) mex ++;
    return f[x] = mex;
}
int main()
{
    int n,ans = 0;
    memset(f,-1,sizeof(f));
    cin >> n;
    for(int i = 1;i <= n;i++) {
        int x;
        cin >> x;
        ans ^= sg(x);
    }
    if(ans) cout << "Yes" << endl;
    else cout << "No" << endl;
    return 0;
}