初阶数据结构（四）带头双向链表

博主csdn个人主页：小小unicorn
⏩专栏分类：数据结构
代码仓库：小小unicorn的代码仓库
关注我带你学习编程知识

链表的相关介绍

在之前链表的学习中，我们知道：

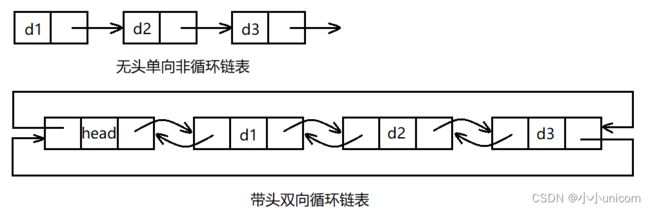
链表的结构一共有八种：带头单向循环链表、带头单向非循环链表、带头双向循环链表、带头双向非循环链表、无头单向循环链表、无头单向非循环链表、无头双向循环链表、无头双向非循环链表。

然而在这八种结构中，我们只挑两种来进行刨析，即无头单向非循环链表和带头双向循环链表。

不带头单向非循环链表：结构简单，一般不会用来存储数据。实际上更多是作为其他数据结构的子结构，如哈希桶、图的链接表等等。此外，这种结构在笔试面试中出现很多。

带头双向循环链表：结构最复杂，一般用在单独存储数据。实际中使用的链表数据结构都是带头双向循环链表。另外，这个结构虽然复杂，但是使用代码实现以后会发现结构会带来很多优势，实现反而简单了。

初始化链表

首先，我们还是需要先定义一个结点类型，与单向链表相比，双向链表的结点类型中需要多出一个前驱指针，用于指向前面一个结点，实现双向。

typedef int LTDataType;//存储的数据类型

typedef struct ListNode
{
	LTDataType data;//数据域
	struct ListNode* prev;//前驱指针
	struct ListNode* next;//后继指针
}ListNode;

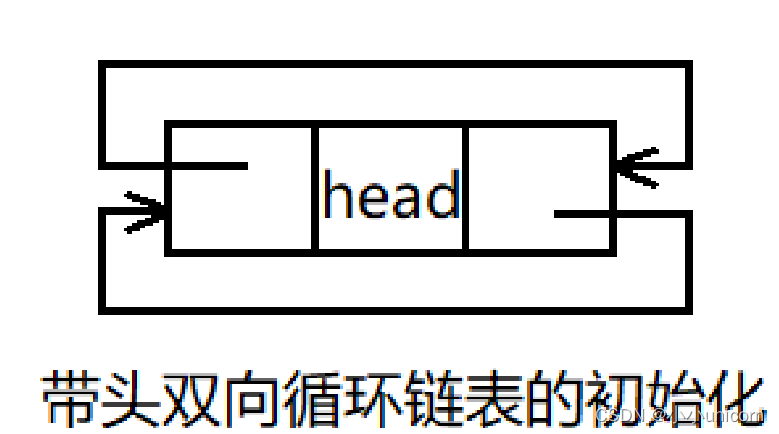
然后我们需要一个初始化函数，对双向链表进行初始化，在初始化的过程中，需要申请一个头结点，头结点的前驱和后继指针都指向自己，使得链表一开始便满足循环。

//创建一个新结点
ListNode* BuyListNode(LTDataType x)
{
	ListNode* node = (ListNode*)malloc(sizeof(ListNode));
	if (node == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	node->data = x;//新结点赋值
	node->prev = NULL;
	node->next = NULL;

	return node;//返回新结点
}

//初始化链表
ListNode* ListInit()
{
	ListNode* phead = BuyListNode(-1);//申请一个头结点，头结点不存储有效数据
	//起始时只有头结点，让它的前驱和后继都指向自己
	phead->prev = phead;
	phead->next = phead;
	return phead;//返回头结点
}

销毁链表

销毁链表，从头结点的后一个结点处开始向后遍历并释放结点，直到遍历到头结点时，停止遍历并将头结点也释放掉。

//销毁链表
void ListDestroy(ListNode* phead)
{
	assert(phead);

	ListNode* cur = phead->next;//从头结点后一个结点开始释放空间
	ListNode* next = cur->next;//记录cur的后一个结点位置
	while (cur != phead)
	{
		free(cur);
		cur = next;
		next = next->next;
	}
	free(phead);//释放头结点
}

打印双向链表

打印双向链表时也是从头结点的后一个结点处开始向后遍历并打印，直到遍历到头结点处时便停止遍历和打印（头结点数据不打印）。

//打印双向链表
void ListPrint(ListNode* phead)
{
	assert(phead);

	ListNode* cur = phead->next;//从头结点的后一个结点开始打印
	while (cur != phead)//当cur指针指向头结点时，说明链表以打印完毕
	{
		printf("%d ", cur->data);
		cur = cur->next;
	}
	printf("\n");
}

查找元素

给定一个值，在链表中寻找与该值相同的结点，若找到了，则返回结点地址；若没有找到，则返回空指针(NULL)。

//查找元素
ListNode* ListFind(ListNode* phead, LTDataType x)
{
	assert(phead);

	ListNode* cur = phead->next;//从头结点的后一个结点开始查找
	while (cur != phead)//当cur指向头结点时，说明链表已遍历完毕
	{
		if (cur->data == x)
		{
			return cur;//返回目标结点的地址
		}
		cur = cur->next;
	}
	return NULL;//没有找到目标结点
}

增加节点

头插

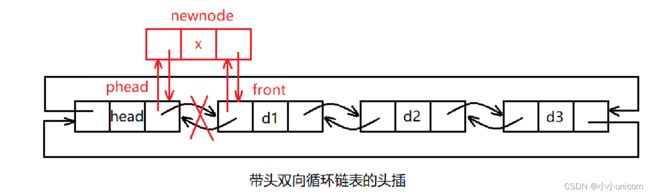
头插，即申请一个新结点，将新结点插入在头结点和头结点的后一个结点之间即可。

//头插
void ListPushFront(ListNode* phead, LTDataType x)
{
	assert(phead);

	ListNode* newnode = BuyListNode(x);//申请一个结点，数据域赋值为x
	ListNode* front = phead->next;//记录头结点的后一个结点位置
	//建立新结点与头结点之间的双向关系
	phead->next = newnode;
	newnode->prev = phead;
	//建立新结点与front结点之间的双向关系
	newnode->next = front;
	front->prev = newnode;
}

尾插

尾插，申请一个新结点，将新结点插入到头结点和头结点的前一个结点之间即可。因为链表是循环的，头结点的前驱指针直接指向最后一个结点，所以我们不必遍历链表找尾。

//尾插
void ListPushBack(ListNode* phead, LTDataType x)
{
	assert(phead);

	ListNode* newnode = BuyListNode(x);//申请一个结点，数据域赋值为x
	ListNode* tail = phead->prev;//记录头结点的前一个结点的位置
	//建立新结点与头结点之间的双向关系
	newnode->next = phead;
	phead->prev = newnode;
	//建立新结点与tail结点之间的双向关系
	tail->next = newnode;
	newnode->prev = tail;
}

在指定位置插入

在直到位置插入结点，准确来说，是在指定位置之前插入一个结点。我们只需申请一个新结点插入到指定位置结点和其前一个结点之间即可。

//在指定位置插入结点
void ListInsert(ListNode* pos, LTDataType x)
{
	assert(pos);

	ListNode* before = pos->prev;//记录pos指向结点的前一个结点
	ListNode* newnode = BuyListNode(x);//申请一个结点，数据域赋值为x
	//建立新结点与before结点之间的双向关系
	before->next = newnode;
	newnode->prev = before;
	//建立新结点与pos指向结点之间的双向关系
	newnode->next = pos;
	pos->prev = newnode;
}

删除节点

头删

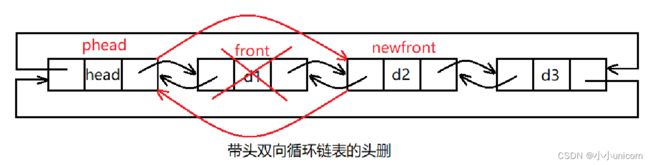
头删，即释放头结点的后一个结点，并建立头结点与被删除结点的后一个结点之间的双向关系即可。

//头删
void ListPopFront(ListNode* phead)
{
	assert(phead);
	assert(phead->next != phead);

	ListNode* front = phead->next;//记录头结点的后一个结点
	ListNode* newfront = front->next;//记录front结点的后一个结点
	//建立头结点与newfront结点之间的双向关系
	phead->next = newfront;
	newfront->prev = phead;
	free(front);//释放front结点
}

尾删

尾删，即释放最后一个结点，并建立头结点和被删除结点的前一个结点之间的双向关系即可。

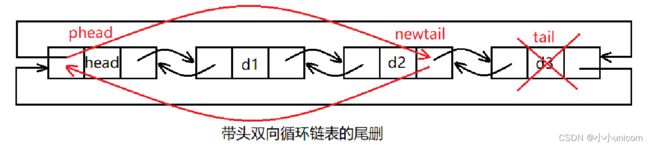
//尾删
void ListPopBack(ListNode* phead)
{
	assert(phead);
	assert(phead->next != phead);

	ListNode* tail = phead->prev;//记录头结点的前一个结点
	ListNode* newtail = tail->prev;//记录tail结点的前一个结点
	//建立头结点与newtail结点之间的双向关系
	newtail->next = phead;
	phead->prev = newtail;
	free(tail);//释放tail结点
}

在指定位置删除

删除指定位置结点，释放掉目标结点后，建立该结点前一个结点和后一个结点之间的双向关系即可。

//删除指定位置结点
void ListErase(ListNode* pos)
{
	assert(pos);

	ListNode* before = pos->prev;//记录pos指向结点的前一个结点
	ListNode* after = pos->next;//记录pos指向结点的后一个结点
	//建立before结点与after结点之间的双向关系
	before->next = after;
	after->prev = before;
	free(pos);//释放pos指向的结点
}

链表判空

链表判空，即判断头结点的前驱或是后驱指向的是否是自己即可。

//链表判空
bool ListEmpty(ListNode* phead)
{
	assert(phead);

	return phead->next == phead;//当链表中只有头结点时为空
}

获取链表元素

获取链表中的元素个数，即遍历一遍链表，统计结点的个数（头结点不计入）并返回即可。

//获取链表中的元素个数
int ListSize(ListNode* phead)
{
	assert(phead);

	int count = 0;//记录元素个数
	ListNode* cur = phead->next;//从头结点的后一个结点开始遍历
	while (cur != phead)//当cur指向头结点时，遍历完毕，头结点不计入总元素个数
	{
		count++;
		cur = cur->next;
	}
	return count;//返回元素个数
}