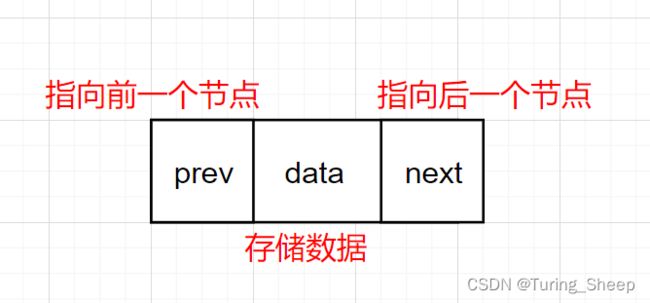
第四章 带头双向链表的讲解与实现

初阶数据结构

第一章 时间复杂度和空间复杂度
第二章 动态顺序表的实现
第三章 单向链表的讲解与实现
第四章 带头双向链表的讲解与实现

---

---

前言

上一章节中，我们学习了无头指针的单向链表的逻辑和代码实现，但是我们发现这种单向结构在使用的时候是存在很大的弊端的，比如说我们无法通过中间的某个节点直接找到他前一个节点，只能从头开始遍历。这是非常低效地一种方式。为了解决链表的单向性，我们本章节将介绍一个双向链表。
同时，由于上一章节中，我们的链表是不带头节点的，即没有哨兵位。因此，我们在实现接口函数的时候大概率要单独讨论链表为空的情况。那么本章节将介绍一种带头的链表，从而统一各种情况下的处理方式。
综上，我们就引出了我们今天的主题：带头双向链表

---

一、什么是头节点（哨兵位）

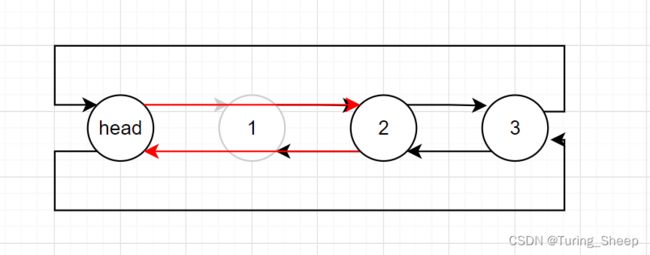
在上述的双向链表中，在第一个节点的前面多出了一个节点，这个节点的数据域是没有用处的。但是头节点的指针域具有很重要的作用，它的指向后方节点的指针域记录了第一个节点的地址。指向前方节点的指针域记录了最后一个节点的地址。
那么这样设置一个头节点有什么作用呢？
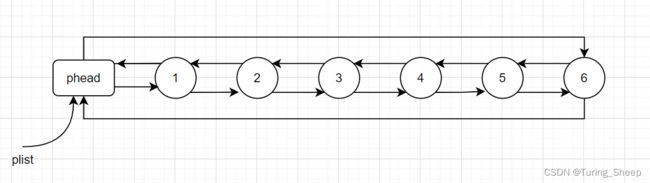
最大的作用就是让链表中的节点个数始终不为0，什么意思呢？我们看下方图示：

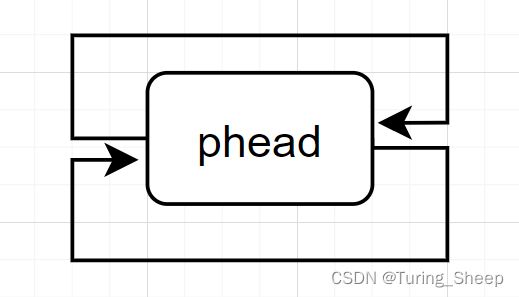
我们发现，即使链表为空，头节点依旧存在，其妙处将在下面实现接口函数的时候体现出来。

二、双向链表结点的定义

typedef int ElementType;
typedef struct DListNode
{
    struct DListNode* next;
    struct DlistNode* prev;
    ElementType data;
}DLTnode;

三、接口函数的实现

1、初始化

初始化，即开辟一个头节点，然后让这个头节点的前后指针域都指向自己。

DLTnode* DListInit()
{
    DLTnode* phead = (DLTnode*)malloc(sizeof(DLTnode));
    phead->next = phead;
    phead->prev = phead;
    return phead;
}

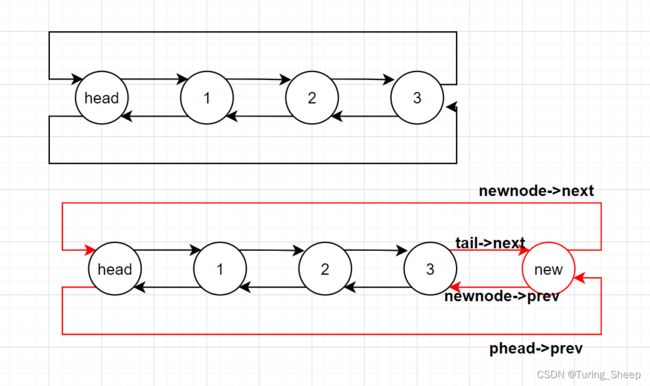
2、尾插

尾插的逻辑如下图所示：

void DListPushBack(DLTnode* phead, ElementType dat)
{
    assert(phead != NULL);
    DLTnode* newnode = (DLTnode*)malloc(sizeof(DLTnode));
    newnode->data = dat;
    DLTnode* tail = phead->prev;
    tail->next = newnode;
    newnode->prev = tail;
    newnode->next = phead;
    phead->prev = newnode;
}

我们发现上述代码并没有单独讨论空链表的情况，这就是头节点的好处，之所以不用讨论就是因为节点的个数不可能为0，最少也包括一个头节点。

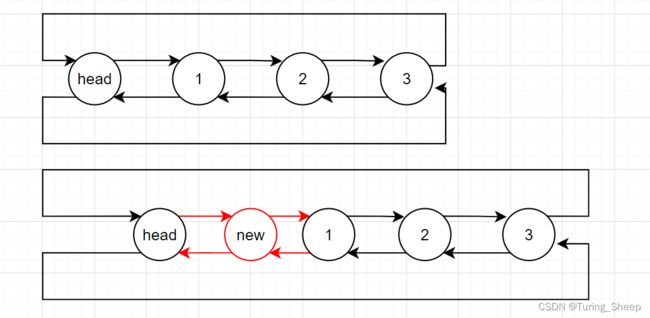
3、头插

void DListPushFront(DLTnode* phead, ElementType dat)
{
    assert(phead != NULL);
    DLTnode* newnode = (DLTnode*)malloc(sizeof(DLTnode));
    newnode->data = dat;
    newnode->next = phead->next;
    phead->next->prev = newnode;
    phead->next = newnode;
    newnode->prev = phead;

}

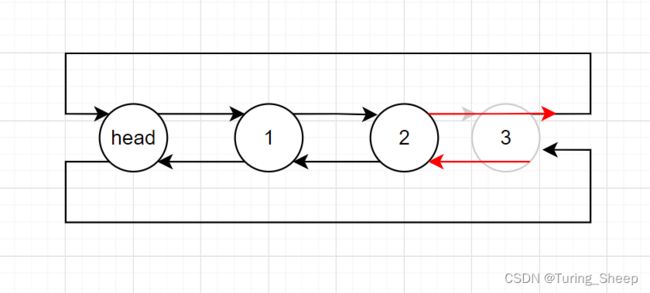
4、尾删

void DListPopBack(DLTnode* phead)
{
    assert(phead != NULL);
    assert(phead->next!=phead);//防止删掉头节点
    DLTnode* tail = phead->prev;
    DLTnode*tailprev=tail->prev;
    tailprev->next = phead;
    phead->prev = tailprev;
    free(tail);
    tail = NULL;

}

5、头删

void DListPopFront(DLTnode* phead)
{
    assert(phead!=NULL);
    assert(phead->next!=phead);//防止删掉头节点
    DLTnode* First = phead->next;
    DLTnode* second = phead->next->next;
    phead->next = second;
    second->prev = phead;
    free(First);
    First = NULL;
}

6、打印

打印的逻辑非常简单，就是从头遍历一遍即可，但是需要注意的是，这是一个循环链表，如果我们不加限制条件的话，他会一直循环下去。所以，我们这里需要加上判断条件。

void DListPrint(DLTnode* phead)
{
    assert(phead != NULL);
    DLTnode* cur = phead->next;
    while (cur != phead)
    {
        printf("%d ", cur->data);
        cur = cur->next;
    }
    printf("\n");
    
}

7、查找

逻辑同查找一致。

DLTnode* DListFind(DLTnode* phead, ElementType dat)
{
    assert(phead!=NULL);
    DLTnode* cur = phead->next;
    while (cur != phead)
    {
        if (cur->data == dat)
        {
            return cur;
        }
        else
        {
            cur = cur->next;
        }
    }
    return NULL;
}

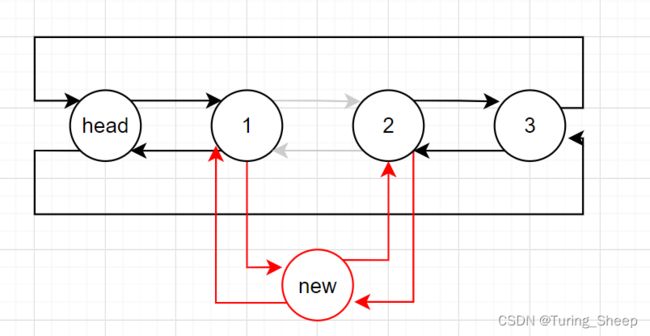
8、随机插入

void DListInsert(DLTnode*pos,ElementType dat)
{
    DLTnode* newnode = (DLTnode*)malloc(sizeof(DLTnode));
    newnode->data = dat;
    DLTnode* posprev = pos->prev;
    posprev->next = newnode;
    newnode->prev = posprev;
    newnode->next = pos;
    pos->prev = newnode;
}

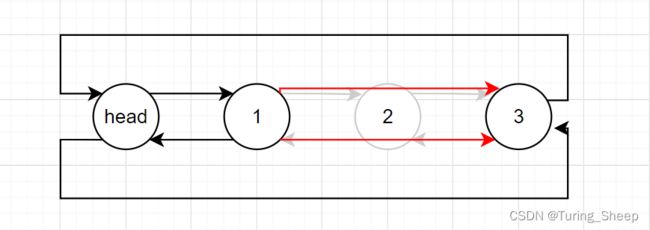
9、随机删除

void DListErase(DLTnode*pos)
{
    DLTnode*posprev = pos->prev;
    DLTnode* posnex = pos->next;
    posprev->next = posnex;
    posnex->prev = posprev;
    free(pos);
    pos = NULL;
}

10、销毁

销毁的逻辑和单链表一样，逐个遍历，逐个销毁，但是注意野指针问题！！

void DListDestory(DLTnode** pphead)
{
    DLTnode* cur = (*pphead)->next;
    while (cur != *pphead)
    {
        DLTnode* curnex = cur->next;
        free(cur);
        cur = curnex;
    }
    free(*pphead);
    *pphead = NULL;
    cur = NULL;
}

四、顺序表和链表的对比

1、顺序表：

（1）优点：

• 支持利用下标的偏移来访问顺序表中的任意位置。
• CPU高速缓存命中率更高。（稍后会讲到）

（2）缺点：

• 数据的插入消耗较多时间，时间复杂度为O(N)。
• 顺序表的容量涉及到扩容的问题：
  • 增容的过程中会造成一定程度的损耗。
  • 为了避免频繁地扩容，我们一般会按照倍数去增加，那么最终剩余的空间一般较多，造成了严重的空间浪费。

2、链表（双向带头循环链表）：

（1）优点：

• 任意位置插入删除时，时间效率高，时间复杂度为O(1)
• 不存在容量的概念，按需申请释放空间。

（2）缺点：

• 不支持利用下标的偏移来随机访问，这就意味着很多算法无法使用链表结构。
• 链表中存储一个值的同时，还需要存储链接指针，这也有一定的消耗。
• CPU高速缓存命中率低

3、什么是缓存命中

（1）什么是缓存

我们知道，cpu会调用内存中的数据来执行计算，现在的CPU性能越来越高效，计算速度飞快。这也导致其调用内存中的数据的速度增加。但是内存由于存储的数据量很大，所以晶体管的数量很大，这就导致在物理上延缓了内存的传输数据的速度。
由于二者速度差距巨大，就导致了CPU会“等待”内存传输数据的情况。这样就造成了时间上的浪费，CPU的性能也就无法充分的发挥。
为了解决这个问题，我们就需要解决二者速度差的问题，因此我们就需要提高数据传输的速度。但是，物理上的晶体管数量无法减少，我们就无法提速。因此，我们在二者之间搭建一片缓冲区域，即缓存。

（2）存储器的结构与高速命中

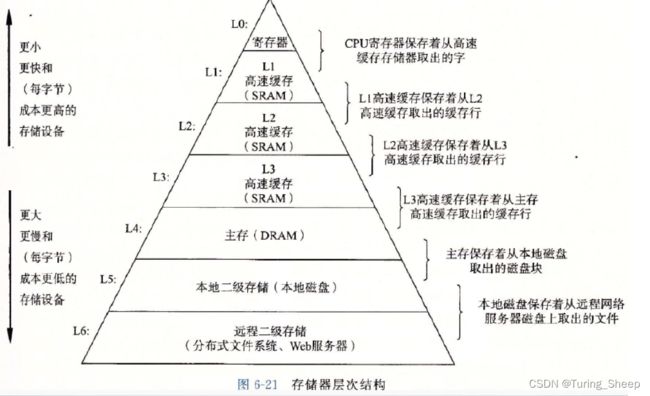
从下到上，各种存储器的内存逐渐降低，数据传输速度逐级增高。这要就在CPU和内存之间搭建了**“楼梯”。
那么每次CPU会从寄存器中读取数据，这二者的速度差距已经大大缩小了。我们以一个数组为例，我们想对第一个元素进行计算，我们不仅会把第一个元素所对的内存传输到寄存器，还会把其相邻的内存空间传输到寄存器中作为备用，每次传输到寄存器中的数据的大小取决于电脑的相应配置。
这样，我们在CPU访问完第一元素后，假设我们还需要计算第二个元素，我们又恰好在寄存器中存储了第二个元素的内存信息。CPU便可直接调用，而无需寄存器再去读取。这就叫缓存命中**。
因此，我们发现缓存命中的关键在于数据相邻存储。但是，链表不是相邻存储的，所以顺序表和链表相比，后者的缓存命中率大大降低。