JavaSE及数据结构---初识Java
目录
一、工作领域
企业级系统
Web开发领域
android平台应用
大数据平台开发
二、语言特性
1. 简单性
2. 面相对象
3. 分布式(微服务)
4. 健壮性
5. 安全性
6. 体系结构中立
7. 可移植性
8. 解释性
9. 高性能
10. 多线程
11. 动态性
三、Java的程序结构
四、Java的程序运行
五、标识符
六、关键字
七、初始集合框架
1、什么是集合框架
2. 背后所涉及的数据结构以及算法
2.1 什么是数据结构
2.2 容器背后对应的数据结构
2.3 相关java知识
2.4 什么是算法
八、时间和空间复杂度
1、时间复杂度
1.1概念
1.2大O的渐进表示法
1.3常见时间复杂度计算举例
2.空间复杂度
2.1概念
一、工作领域
Java语言目前在 IT 领域的应用是非常广泛的,掌握 Java 语言可以从事不少 IT 行业的相关开发岗位,具体包括:
企业级系统
比如大型复杂的企业级软件系统,Java 的安全机制以及跨平台性的优势,其在分布式系统领域开发中有广泛应用,涉及到金融、电信、交通、电子商务、ERP 系统等。
Web开发领域
Java语言在设计初期,赶上了互联网发展的风口,当时就瞄准了互联网开发,凭借稳定的性能表现和较好的扩展性,Java语言一直是大型互联网平台的重要解决方案。
android平台应用
Android是一种智能手机操作系统, Java 是一门非常流行的编程语言。 Android 上的应用程序就是大多是用Java 编写的, Android 的 SDK 大部分就是直接将 Java SDK 翻译过来的,所以具有 Java 基础,也可以快速上手Android 开发。
大数据平台开发
大数据相关的各类框架,比如:Hadoop 、 spark 、 storm 、 flflink 等,以及各种中间件 flflume 、 kafka、 sqoop等,这些框架以及工具等大多数是用 Java 语言开发的,随着大数据技术的落地应用, Java 在大数据领域的应用前景也是比较广阔的。
除上述开发领域外,Java 在游戏领域、人工智能领域、科学计算领域、嵌入式领域也有一定的应用。因此学好Java,将来就业的选择也会非常广泛。
二、语言特性
1. 简单性
Java语法是 C++ 语法的一个 “ 纯净版本 ” ,相当于对 C++ 做了一个减法。这里没有头文件、指针运算(甚至指针语法)、结构、联合、操作符重载、虚基类等等。不仅如此,Java 开发环境远远超出大多数其他编程语言的开发环境。
2. 面相对象
什么是面向对象?
在Java 的世界里,一切皆对象 。比如:人、狗、手机、电脑等都是对象。所谓面相对象,就是依靠对象之间的交互来完成事情,比如:人用手机网上购物,狗吃骨头...Java的面向对象特性与 C++ 旗鼓相当,与 C++ 的主要不同点在于多重继承。在 Java 中,取而代之的是更简单的接口概念。而且与C++ 相比, Java 提供了更丰富的运行时自省功能。
3. 分布式(微服务)
Java有丰富的例程库,用于处理像 HTTP 和 FTP 之类的 TCP/IP 协议。 Java 应用程序能够通过 URL 打开和访问网络上的对象,其便捷程度就好像访问本地文件一样。
4. 健壮性
Java与 C++ 最大的不同在于 Java 采用的指针模型可以消除重写内存和损坏数据的可能性(对于曾经花费几个小时来检查由于指针bug 而引起内存冲突的人来说,一定很喜欢 Java 的这一特性)。不仅如此, Java 编译器能够检测许多在其他语言中仅在运行时才能够检测出来的问题。
5. 安全性
Java适用于网络 / 分布式环境。为了达到这个目标,在安全性方面投入了大量的精力。使用 Java 可以构建防病毒、防篡改的系统。
从一开始,Java就设计成能够防范常见的各种攻击:
- 运行时堆栈溢出。蠕虫和病毒常用的攻击手段。
- 破坏自己进程空间之外的内存。
- 未经授权读写文件
6. 体系结构中立
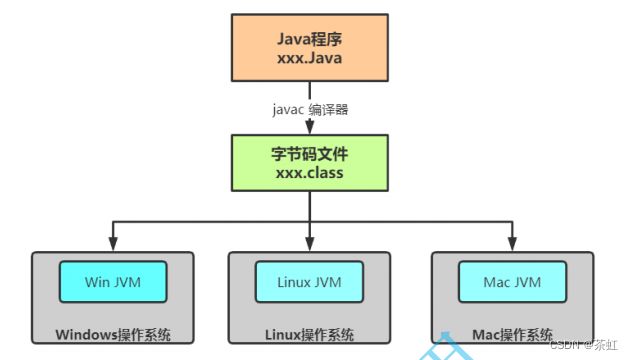
编译器生成一个体系结构中立的目标文件格式,按照该中规范生成的文件,只要有Java 运行时系统,这些编译后的代码就可以在许多处理器上运行。Java 编译器通过生成与特定计算机体系结构无关的字节码指令来实现 这一特性 。精心设计的字节码不仅可以很容易的在任何机器上解释执行,而且还可以动态地翻译成本地机器代码。这就是为什么可以:“Wrice once , Run anywhere” 。
而且其他语言编写的程序,在编译后如果能够严格按照字节码文件的规范生成.class文件,也可以在JVM上运行。
7. 可移植性
与C/C++ 不同, Java 规范中没有 “ 依赖具体实现的地方 ” 。 基本数据类型的大小以及有关运算都做了明确的说 明 。例如, Java 中的 int 永远是 32 位的整数,而在 C/C++ 中, int 可能是 16 位整数、 32 位整数,也可能是编译器提供商指定的其他大小。在Java 中,数据类型具有固定的大小,这消除了代码移植时令人头疼的主要问题。
8. 解释性
Java为了实现与平台无关,自己维护了一套基于栈架构的指令集, Java 源代码经过编译之后,字节码文件中的指令就是按照自己的指令集来组织的,但是在具体硬件环境中运行时,系统并不能识别,因为Java 程序在执行时,Java 解释器会逐条的将字节码文件中的指令翻译成 CPU 的指令集。
9. 高性能
边解释边执行,垃圾会说等导致了Java 代码运行效率偏低,近年来 JVM 也在不断的优化,比如: JIT( 即时编译器) ,热点代码探测,让 Java 程序的执行效率大幅提高,在有些场合不亚于 C/C++ 。
10. 多线程
Java在当时很超前。它是第一个支持并发程序设计的主流语言。多线程可以带来更好的交互响应和实时行为。并发程序设计绝非易事,但是Java 在这方面表现出色,可以很好的管理这个工作。
11. 动态性
Java与 C/C++ 相比更加具有动态性。它能够适应不断发展的环境。库中可以自由的添加新方法和实例变量,而对客户端没有任何影响。在Java 中找出运行时类型信息十分简单(反射的特性,后续会学到)
因此:Java 不仅仅是一门编程语言,也是一个由一些列计算机软件和规范组成的技术体系 。
三、Java的程序结构
一个完整的Java 程序的结构, Java 程序的结构由如下三个部分组成:
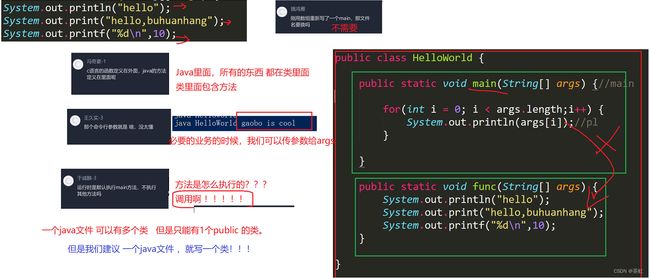
1.源文件(扩展名为*.java):源文件带有类的定义。类用来表示程序的一个组件,小程序或许只会有一个类。类的内容必须包含在花括号里面。2.类:类中带有一个或多个方法。方法必须在类的内部声明。3.方法:在方法的花括号中编写方法应该执行的语句。总结一下:类存在于源文件里面;方法存在于类中;语句存在于方法中。
注意:在一个源文件中只能有一个public 修饰的类,而且源文件名字必须与 public 修饰的类名字相同 。
四、Java的程序运行
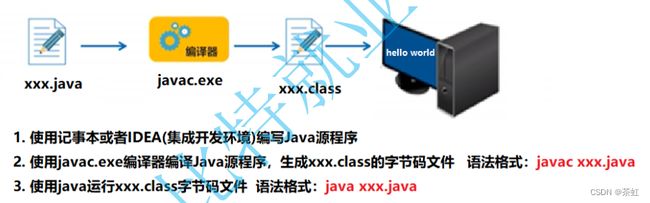
Java是一门半编译型、半解释型语言。先通过 javac 编译程序把源文件进行编译,编译后生成的 .class 文件是由字节码组成的平台无关、面向JVM 的文件。最后启动 java 虚拟机来运行 .class 文件,此时 JVM 会将字节码转换成平台能够理解的形式来运行。
注意:在运行Java程序前,必须先安装好JDK(Java Development Kit即Java开发工具包),JDK里面就包含了javac和java工具,Java程序最终是在JVM(Java虚拟机)中运行的。
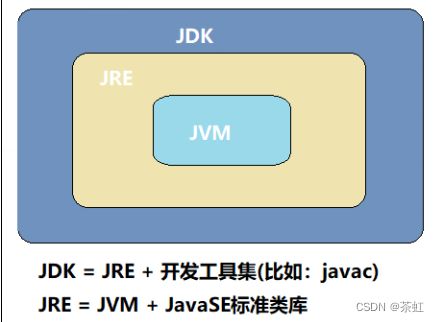
JDK、 JRE 、 JVM 之间的关系?
- JDK(Java Development Kit):Java开发工具包,提供给Java程序员使用,包含了JRE,同时还包含了编译 器javac与自带的调试工具Jconsole、jstack等。
- JRE(Java Runtime Environment):Java运行时环境,包含了JVM,Java基础类库。是使用Java语言编写程序运行的所需环境。
- JVM:Java虚拟机,运行Java代码
五、标识符
在上述程序中,Test 称为类名, main 称为方法名,也可以将其称为标识符,即: 在程序中由用户给类名、方法名或 者变量所取的名字 。
【 硬性规则 】
标识符中可以包含:字母、数字以及 下划线和 $ 符号等等。
注意:标识符不能以数字开头,也不能是关键字,且严格区分大小写 。
【 软性建议 】
- 类名:每个单词的首字母大写(大驼峰)
- 方法名:首字母小写,后面每个单词的首字母大写(小驼峰)
- 变量名:与方法名规则相同
六、关键字
七、初始集合框架
1、什么是集合框架
官方教程
Trail: Collections (The Java™ Tutorials) (oracle.com)![]() https://docs.oracle.com/javase/tutorial/collections/index.html
https://docs.oracle.com/javase/tutorial/collections/index.html
Java 集合框架 Java Collection Framework ,又被称为容器 container ,是定义在 java.util 包下的一组接口 interfaces和其实现类 classes 。其主要表现为将多个元素 element 置于一个单元中,用于对这些元素进行快速、便捷的存储 store 、检索 retrieve 、管理 manipulate ,即平时我们俗称的增删查改 CRUD 。例如,一副扑克牌( 一组牌的集合 ) 、一个邮箱 ( 一组邮件的集合 ) 、一个通讯录 ( 一组姓名和电话的映射关系 ) 等等。
类和接口总览
2. 背后所涉及的数据结构以及算法
2.1 什么是数据结构
数据结构(Data Structure) 是计算机存储、组织数据的方式,指相互之间存在一种或多种特定关系的数据元素的集合。
2.2 容器背后对应的数据结构
该阶段,我们主要学习以下容器,每个容器其实都是对某种特定数据结构的封装,大概了解一下,后序详细说明并模拟实现:
1. Collection : 是一个接口,包含了大部分容器常用的一些方法
2. List : 是一个接口,规范了 ArrayList 和 LinkedList 中要实现的方法
ArrayList : 实现了 List 接口,底层为动态类型顺序表
LinkedList :实现了 List 接口,底层为双向链表
3. Stack :底层是栈,栈是一种特殊的顺序表
4. Queue :底层是队列,队列是一种特殊的顺序表
5. Deque :是一个接口
6. Set :集合,是一个接口,里面放置的是 K 模型
HashSet :底层为哈希桶,查询的时间复杂度为 O(1)
TreeSet :底层为红黑树,查询的时间复杂度为 O(log2N),关于 key 有序
7. Map :映射,里面存储的是 K-V 模型的键值对
HashMap :底层为哈希桶,查询时间复杂度为 O(1)
TreeMap :底层为红黑树,查询的时间复杂度为O(log2N),关于key 有序
2.3 相关java知识
1. 泛型 Generic2. 自动装箱 autobox 和自动拆箱 autounbox3. Object 的 equals 方法4. Comparable 和 Comparator 接口
2.4 什么是算法
算法(Algorithm): 就是定义良好的计算过程,他取一个或一组的值为输入,并产生出一个或一组值作为输出。简单来说算法就是一系列的计算步骤,用来将输入数据转化成输出结果。
八、时间和空间复杂度
1、时间复杂度
1.1概念
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个数学函数 ,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
1.2大O的渐进表示法
// 请计算一下func1基本操作执行了多少次?
void func1(int N)
{ int count = 0;
for (int i = 0; i < N ; i++)
{
for (int j = 0; j < N ; j++)
{
count++;
}
}
for (int k = 0; k < 2 * N ; k++)
{
count++;
}
int M = 10;
while ((M--) > 0)
{
count++;
}
System.out.println(count);
}实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
大O 符号( Big O notation ):是用于描述函数渐进行为的数学符号
1.3常见时间复杂度计算举例
// 计算func2的时间复杂度?
void func2(int N)
{
int count = 0;
for (int k = 0; k < 2 * N ; k++)
{
count++;
}
int M = 10;
while ((M--) > 0)
{
count++;
}
System.out.println(count);
}// 计算func3的时间复杂度?
void func3(int N, int M)
{ int count = 0;
for (int k = 0; k < M; k++)
{
count++;
}
for (int k = 0; k < N ; k++)
{
count++;
}
System.out.println(count);
}// 计算func4的时间复杂度?
void func4(int N)
{
int count = 0;
for (int k = 0; k < 100; k++)
{
count++;
}
System.out.println(count);
}// 计算bubbleSort的时间复杂度?
void bubbleSort(int[] array)
{
for (int end = array.length; end > 0; end--)
{
boolean sorted = true;
for (int i = 1; i < end; i++)
{
if (array[i - 1] > array[i])
{
Swap(array, i - 1, i);
sorted = false;
}
}
if (sorted == true)
{
break;
}
}
}// 计算binarySearch的时间复杂度?
int binarySearch
(
int[] array, int value)
{
int begin = 0;
int end = array.length - 1;
while (begin <= end)
{
int mid = begin + ((end-begin) / 2);
if (array[mid] < value)
begin = mid + 1;
else if
(array[mid] > value) end = mid - 1;
else
return mid;
}
return -1;
}// 计算阶乘递归factorial的时间复杂度?
long factorial(int N)
{
return N < 2 ? N : factorial(N-1) * N;
}// 计算斐波那契递归fibonacci的时间复杂度?
int fibonacci(int N)
{
return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);
}【 实例答案及分析 】1. 实例 1 基本操作执行了 2N+10 次,通过推导大 O 阶方法知道,时间复杂度为 O(N)2. 实例 2 基本操作执行了 M+N 次,有两个未知数 M 和 N ,时间复杂度为 O(N+M)3. 实例 3 基本操作执行了 100 次,通过推导大 O 阶方法,时间复杂度为 O(1)4. 实例 4 基本操作执行最好 N 次,最坏执行了 (N*(N-1))/2 次,通过推导大 O 阶方法 + 时间复杂度一般看最坏,时间复杂度为 O(N^2)5. 实例 5 基本操作执行最好 1 次,最坏次,时间复杂度为 O( log2N)ps: 在算法分析中表示是底数 为 2 ,对数为 N ,有些地方会写成 lgN 。(建议通过折纸查找的方式讲解 logN 是怎么计算出来的) ( 因为二分查找每次排除掉一半的不适合值, 一次二分剩下: n/2两次二分剩下: n/2/2 = n/4)6. 实例 6 通过计算分析发现基本操作递归了 N 次,时间复杂度为 O(N) 。7. 实例 7 通过计算分析发现基本操作递归了2的N次方次,时间复杂度为O(2的N次方 )。(建议画图递归栈帧的二叉树讲解)
2.空间复杂度
2.1概念
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少 bytes 的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟实践复杂度类似,也使用大 O 渐进表示法 。
2.2举例
// 计算bubbleSort的空间复杂度?
void bubbleSort(int[] array)
{
for (int end = array.length; end > 0; end--)
{
boolean sorted = true;
for (int i = 1; i < end; i++)
{
if (array[i - 1] > array[i])
{
Swap(array, i - 1, i);
sorted = false;
}
}
if (sorted == true)
{
break;
}
}
}// 计算fibonacci的空间复杂度?
int[] fibonacci(int n)
{
long[] fibArray = new long[n + 1];
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; i++)
{
fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
}
return fibArray;
}// 计算阶乘递归Factorial的空间复杂度?
long factorial(int N)
{
return N < 2 ? N : factorial(N-1)*N;
}【 实例答案及分析 】1. 实例 1 使用了常数个额外空间,所以空间复杂度为 O(1)2. 实例 2 动态开辟了 N 个空间,空间复杂度为 O(N)3. 实例 3 递归调用了 N 次,开辟了 N 个栈帧,每个栈帧使用了常数个空间。空间复杂度为 O(N)