数据结构中的队列以及相关的题型
队列
- 1.队列的概念
- 2.队列的使用
- 3.队列的模拟实现
- 4.队列循环
-
- 4.1循环队列的引入
- 4.2 循环队列使用
- 4.3 如何区分空与满
- 5.相关题型
-
- 5.1. 用队列实现栈。
- 5.2. 用栈实现队列。
- 5.3. 实现一个最小栈
1.队列的概念
只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出
入队列:进行插入操作的一端称为队尾
出队列:进行删除操作的一端称为队头
2.队列的使用
底层使用LinkedList实现的

注意:Queue是个接口,在实例化时必须实例化对象LinkedList的对象,因为LinkedList实现了Queue接口
package Day1027;
import java.util.LinkedList;
import java.util.Queue;
public class Queue {
public static void main(String[] args) {
Queue<Integer> q = new LinkedList<>();
q.offer(1);
q.offer(2);
q.offer(3);
q.offer(3);
q.offer(4);
q.offer(5); //从队尾入队列
System.out.println(q.size());
System.out.println(q.peek()); //获取队头元素
q.poll();
System.out.println(q.poll);//从队头出队列,并将删除元素返回
if(q.isEmpty()){
System.out.println("队列空");
}else{
System.out.println(q.size());
}
}
}
问题: 队列能使用连续空间吗?
使用连续空间实现队列的时候,可以保证入队列操作时间复杂度O(1)
3.队列的模拟实现
队列中既然可以存储元素,那底层肯定要有保存元素的空间。常见的空间类型有:顺序结构和链式结构
public class MyQueue<E>{
public static class Node<E>{
private E value;
private Node<E> next;
public Node(E val){
value = val;
next = null;
}
}
Node<E> front; //标记队头
Node<E> back; //标记队尾
int size;
public boolean offer(E e){
Node<E> node = new Node<>(e);
if(null == front) {
front = node;
}else{
back.next =node;
}
back = node;
size++;
return true;
}
public E poll(){
if(0 == size){
throw new RuntimeException("队列为空,无法出队列");
}
Node<E> deINode = front;
front = front.next;
if(null == front){
back = null;
}
size--;
return deINode.value;
}
public E peek(){
if(0==size){
throw new RuntimeException("队列为空,无法获取队头元素");
}
return front.value;
}
public boolean isEmpty(){
return 0 == size;
}
public int size(){
return size;
}
}
}
4.队列循环
4.1循环队列的引入
出队列的方式:
方法一:保持front不动,始终放在0位置,将队头之后的所有元素整体往前移一位,最后将所有元素整体往前移一位,最后将rear往前移一位。
时间复杂度为O(N)
方法二:每次出队列中,将front往后移动一位
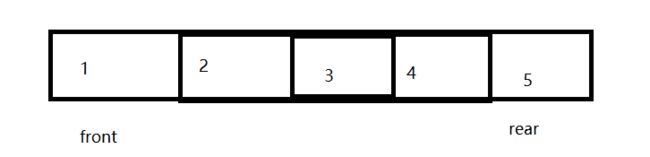
时间复杂度O(1)
缺陷:
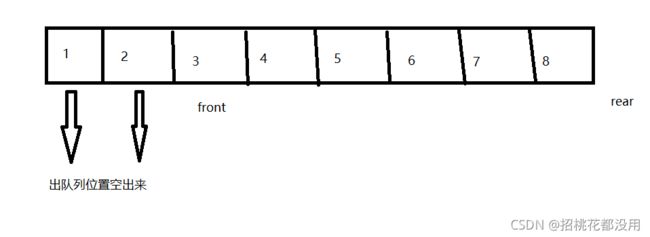
上述现象称为队列的假溢出(元素已经插不进去)
真溢出:队列中有效元素已经和空间大小相等了
为了解决上述使用连续空间实现队列时的假溢出问题===》循环队列
4.2 循环队列使用
环形队列常用数组实现
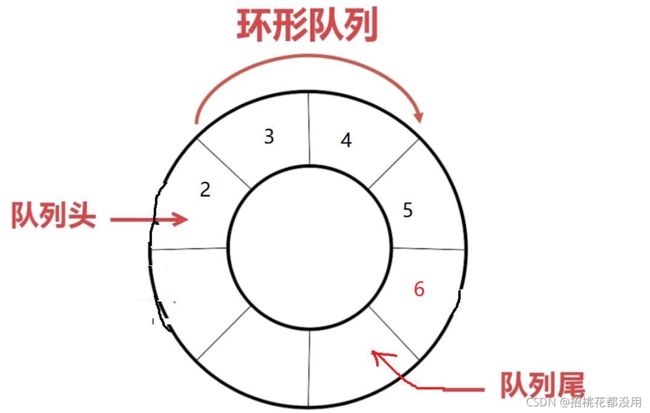
入队列:将元素放在rear队尾的位置,然后rear往后移动
出对列:front往后移动一步,上一个元素出队列
4.3 如何区分空与满

第三种方法:设置一个标志位:
入队列时: rear向下一位移动,将flag = true
出队列时: front 向下一位移动 将flag = false
设计一个循环队列
class MyCircularQueue {
int[] array;
int front;//定义头结点
int rear;//定义尾结点
int count;//定义有效节点
int N;//定义数组长度
public MyCircularQueue(int k) {
array = new int[k];
N = k;
}
public boolean enQueue(int value) {
if(isFull()){
return false;
}
array[rear] = value;
rear++;
if(rear == N){
rear = 0;
}
count++;
return true;
}
public boolean deQueue() {
if(isEmpty()){
return false;
}
front++;
front %= N;
count--;
return true;
}
public int Front() {
if(isEmpty()){
return -1;
}
return array[front];
}
public int Rear() {
if(isEmpty()){
return -1;
}
return array[(rear + N - 1)% N];
}
public boolean isEmpty() {
return 0 == count;
}
public boolean isFull() {
return count == array.length;
}
}
/**
* Your MyCircularQueue object will be instantiated and called as such:
* MyCircularQueue obj = new MyCircularQueue(k);
* boolean param_1 = obj.enQueue(value);
* boolean param_2 = obj.deQueue();
* int param_3 = obj.Front();
* int param_4 = obj.Rear();
* boolean param_5 = obj.isEmpty();
* boolean param_6 = obj.isFull();
*/
5.相关题型
5.1. 用队列实现栈。
class MyStack {
Queue<Integer> queue1;
Queue<Integer> queue1;
public MyStack() {
queue1 = new LinkedList<Integer>;
queue2 = new LinkedList<Integer>;
}
public void push(int x) {
queue2.offer(x);
while(!queue1.isEmpty()){
queue2.offer(queue1.poll());
}
Queue<Integer> temp = queue1;
queue1 = queue2;
queue2 = temp;
}
public int pop() {
return queue1.poll()
}
public int top() {
return queue1.peek;
}
public boolean empty() {
return queue1.isEmpty;
}
}
/**
* Your MyStack object will be instantiated and called as such:
* MyStack obj = new MyStack();
* obj.push(x);
* int param_2 = obj.pop();
* int param_3 = obj.top();
* boolean param_4 = obj.empty();
*/
5.2. 用栈实现队列。
入队列:直接将元素放入s1中
出队列:如果s2是空的,将s1中的所有元素导入到s2中,然后将s2栈顶元素删除掉
获取队头元素:如果s2是空的,将s1中的所有元素导入到s2中,然后获取s2栈顶的元素
void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空,返回 true ;否则,返回 false
class MyQueue {
Deque<Integer> s1;
Deque<Integer> s2;
public MyQueue() {
s1= new LinkedList<Integer>();
s2 = new LinkedList<Integer>();
}
public void push(int x) {
s1.push(x);
}
public int pop() {
if (s2.isEmpty()) {
in2out();
}
return s2.pop();
}
public int peek() {
if (s2.isEmpty()) {
in2out();
}
returns2.peek();
}
public boolean empty() {
return s1.isEmpty() && s2.isEmpty();
}
private void inout() {
while (!s1.isEmpty()) {
s2.push(inStack.pop());
}
}
}
5.3. 实现一个最小栈
入栈,出栈,获取栈顶元素时间复杂度都是O(1),获取栈顶元素中的最小值的时间复杂度是O(1)
方法一:只是用一个栈
入栈 :data
一次性压入两个元素:data 最小值
假设先压入最小值,后压入data
每次压入数据,需要将data与栈中最小值先进行比较
如果 data < 栈中的最小值 压入两个data
如果 data >= 栈中的最小值 先压入栈中原来的最小值,然后再压入data
获取栈顶元素:peek()
方法二:用两个栈s1 s2模拟实现
s1:放有效数据
s2:放栈中最小值
入栈:如果s2是空的,将元素往s1 和 s2各压入一份
将data 与 s2栈顶元素进行比较
data < s2 栈顶元素,将data往s1和s2各压入一份
data >= s2 栈顶元素,将data和s1中压入
class MinStack {
Stack<Integer> a;//用来入栈
Stack<Integer> b;//储存最小元素
public MinStack() {
a = new Stack();
b = new Stack();
}
public void push(int val) {
//如果b为空或者即将入栈元素小于等于b的栈顶元素,此时a,b同时入栈val
if(b.empty() || b.peek() >= val){
b.push(val);
}
a.push(val);
}
//删除栈顶元素也要考虑大小问题
public void pop() {
if(b.peek() >= a.peek()){
b.pop();
}
a.pop();
}
public int top() {
if(a.empty()){
return -1;
}
return a.peek();
}
public int getMin() {
if(b.empty()){
return -1;
}
return b.peek();
}
}