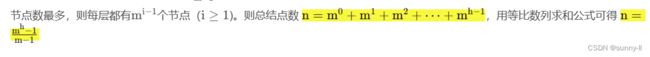【数据结构】树的概念理解和性质推导（保姆级详解，小白必看系列）

目录

一、前言

为什么要学习非线性结构 ---- 树（Tree）

线性结构的优缺点

  优化方案 ----- 树（Tree）

树的讲解流程

 二、树的概念及结构

树的概念

树的相关定义

  树的表示方法

  树在现实中的应用

  树的性质（超重要哦！！）

  性质1：树中的节点数等于所有节点度数加 1

  性质2：度为 m 的树中第 i 层至多有 m^i-1 个节点（i>=1）

  性质3：高度为 h 的 m 叉树至多有  m^h-1/m-1 个节点​

  性质4：具有n个结点的m叉树的最小高度为⌈logm(n*(m-1)+1)⌉

 三、共勉

---

一、前言

         在之前的几篇文章中已经详细的介绍了数据结构中的顺序表、链表、栈、队列、数组等，都是一对一的线性关系。本文将开始介绍一种新的数据结构 --------- 树（一对多的非线性关系）。

         那么肯定有 老铁 要发问啦，有线性结构去存储数据，为什么还要用非线性的结构去存储呢 ？它们之间有什么区别呢 ？ 接下里我将依次给大家解惑，让大家真正的搞懂数据结构，学习起来才有动力。

为什么要学习非线性结构 ---- 树（Tree）

线性结构的优缺点

在线性结构中，无论是顺序存储，还是链式存储，线性表均有其优缺点：

顺序表优点：

1️⃣：顺序存储可以在 O(1) 的时间内找到特定次序的元素（下标的随机访问）

2️⃣：CPU 高速缓存，命中率较高

顺序表缺点： 

1️⃣：顺序存储在，数据中间、头部 的插入和删除元素需要挪动大量元素，需要时间O(n)

2️⃣:  顺序存储时，会出现空间不足，只能进行空间的扩容（异地扩容代价比较大）

链表优点：

1️⃣：在任意位置进行数据的插入和删除的效率高，所需时间为O(1)

2️⃣:  按需申请空间和释放，不存在扩容

链表的缺点：

1️⃣：在寻找特定次序的元素需要从链表头部向后查找，需要时间O(n)

2️⃣:  CPU高速缓存，命中率低 

⭐ ：其实链表和顺序表是一个互补的数据结构
⭐ ：链表详解

⭐ ：顺序表详解

  优化方案 ----- 树（Tree）

⭐：树形结构：很好的结合了顺序表和链表的优点，可以在O(logn)的时间内完成查找、更新、插入、删除等操作，在实际的应用中，很多算法可以借助于树形结构高效的实现很多功能。

树的讲解流程

此时此刻大家肯定很想了解什么是树，在本篇博客中，并不能把所有树的结构在此篇文章中进行详细的介绍，我会通过步步延申的方式去讲解树。

树 ➡ 二叉树➡ 搜索二叉树 ➡ 平衡搜索二叉树 (AVL树和红黑树) ➡ M叉多叉平衡搜索树 (B树和B+树)

 

 二、树的概念及结构

树的概念

1️⃣：树是一种非线性的数据结构，它是由 n (n>=0) 个有限结点组成一个具有层次关系的集合。

2️⃣: 把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下。树根可以发出多个分支，每个分支也可以继续发出分支，树枝之间是不想交的。
3️⃣ ：树有一个特殊的结点，称为根结点，根节点没有前驱结点

4️⃣：除根节点外，其余结点被分为 M (M>0) 个互不相交的集合 T1、T2 … 、Tm，其中每一个集合 Ti (1<=i<=m) 又是一棵结构与树类似的子树，每棵子树的根结点有且只有一个前驱，可以有0个或多个后继

5️⃣：因此，树是递归定义的

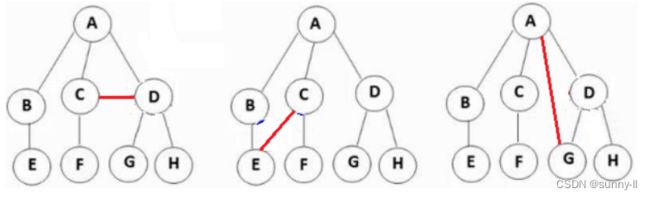
 ⚠ 注意：树形结构中，子树之间不能有交集，否则就不是树形结构

▶  子树 是不相交的

▶  除了根节点外，每个节点有且仅有一个父节点

▶  一棵 N 个节点的树有 N-1 条连

树的相关定义

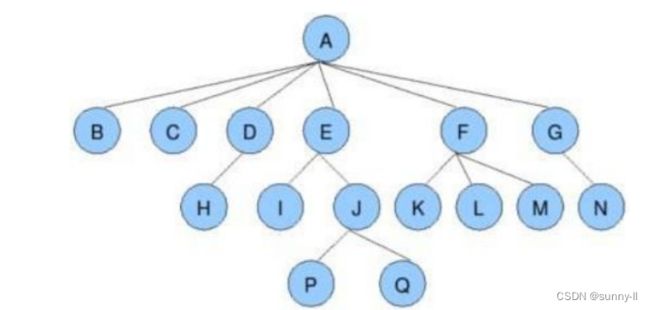
1️⃣ 节点的度：一个节点含有的子树的个数称为该节点的度； 如上图：A 的为6

2️⃣ 叶节点或终端节点：度为0的节点称为叶节点； 如上图：B、C、H、I…等节点为叶节点

3️⃣ 非终端节点或分支节点：度不为0的节点； 如上图：D、E、F、G…等节点为分支节点

4️⃣ 双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点； 如上图：A 是 B 的父节点

5️⃣ 孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点； 如上图：B 是 A 的孩子节点

6️⃣ 兄弟节点：具有相同父节点的节点互称为兄弟节点 (这里指的是亲兄弟，而非表堂兄弟)； 如上图：B、C 是兄弟节点

7️⃣ 树的度：一棵树中，最大的节点的度称为树的度； 如上图：树的度为 6

8️⃣ 节点的层次：从根开始定义起，根为第 1 层，根的子节点为第 2 层， 以此类推；如上图：树的层次为 4

9️⃣ 树的高度或深度：树中节点的最大层次 (这里有 2 种说法：其一，根算 0，其二，根算 1)； 如上图：树的高度为 4
   这里推荐理解其二，因为：
   当要算空树的高度是多少时，按其一的理解，高度是 -1；按其二的理解，高度是 0
   当要算只有一个根节点的树的高度是多少时，按其一的理解，高度是 0；按其二的理解，高度是 1

堂兄弟节点：双亲在同一层的节点互为堂兄弟；如上图：H、I 互为兄弟节点

1️⃣1️⃣ 节点的祖先：从根到该节点所经分支上的所有节点；如上图：A 是所有节点的祖先

1️⃣2️⃣ 子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是 A 的子孙

1️⃣3️⃣ 森林：由 m(m>0) 棵互不相交的树的集合称为森林，并查集就是一个森林
 

  树的表示方法

1️⃣： 树结构相对线性表就比较复杂了，要存储表示起来比较麻烦，既要保存值域，也要保存结点和结点之间的关系。

2️⃣： 实际中树有很多种表示方式如：双亲表示法，孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法。

 ⚠ 注意：对于树的定义其实并不好定义，因为其中有许多未知的因素

1️⃣：明确说明树的度是多少，比如树的度是 6

struct TreeNode
{
	int data;
	//这种结构其实是很浪费的，因为最大的度是6,但往下可能并没有那么多
	struct TreeNode* subs[6];//指针数组
}

⚠ 注意：这种结构其实是很浪费的，因为最大的度是6,但往下可能并没有那么多

 2️⃣：双亲表示法

struct TreeNode
{
	int data;
	struct TreeNode* parent;
}

⚠ 注意：这种结构主要应用在------并查集

 3️⃣：左孩子右兄弟表示法 (比较实用)

typedef int DataTpye;
struct Node
{
	struct Node* _firstChild1;//第一个孩子节点(如有多个孩子，那么只指向最左边的)
	struct Node* _pNextBrother;//指向下一个兄弟节点
	DataType _data;//节点中的数据域
}

  树在现实中的应用

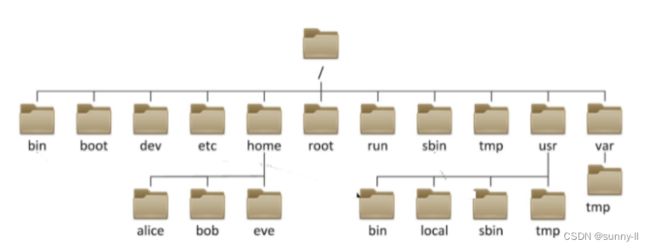
❗ 以下为 Linux 下的目录树 ❗

由此可知，在用树表示目录数据结构中，从根目录到任何数据文件，仅有唯一一条路径可以达到，因为树的结构不是相交的。

  树的性质（超重要哦！！）

 

 性质1：树中的节点数等于所有节点度数加 1

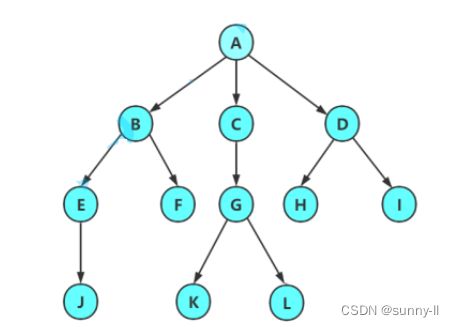
✨：从上图可知，有 12 个节点  ，A的度为：3， B的度为2， C 的度为1， D的度为2， E的度为1， F的度为0， G的度为2， H的度为0 ， I的度为0，J的度为0，K的度0，L的度为0。

✨：由性质 1 可知 树的节点个数 = 每个节点的度数 + 1 

所以上图 树的节点数 = （3+2+1+2+1+0+2+0+0+0+0+0）+1 = 12

  性质2：度为 m 的树中第 i 层至多有 m^i-1 个节点（i>=1）

  性质3：高度为 h 的 m 叉树至多有  m^h-1/m-1 个节点


 

  性质4：具有n个结点的m叉树的最小高度为⌈logm(n*(m-1)+1)⌉

 

 三、共勉

以下就是我对数据结构---树的理解，如果有不懂和发现问题的小伙伴，请在评论区说出来哦，同时我还会继续更新对数据结构-------二叉树，请持续关注我哦！！！！！