简明时序电路分析
我想向大家分享一下如何对简单时序电路进行分析,故本篇博客主要面向数字电子技术初学者,不烧脑。
时序?什么叫时序?
相信看这篇博客的同学们都已经学习过组合逻辑电路,组合逻辑电路的最大特点就是:
在任何时刻,电路的输出状态只取决于同一时刻的输入状态,而与电路原来的状态无关。
那什么叫“时序电路呢?”
所谓时序,就是“时间上的次序”,举个简单的例子:地球人都知道,把大象塞进冰箱分为三步:
- 打开冰箱门
- 把大象放进去
- 关上冰箱门
这时,如果前一个塞大象的人最后没有关上冰箱门,那么下一个塞大象的人只需要做两步:
- 把大象放进去
- 关上冰箱门
咱们意识到,在这个“塞大象”的过程中,前面冰箱门的状态会对后面的人的操作产生影响,所以我们称这个过程是有“记忆”的,或者说是“时序”的,由此我们可以引出时序电路的概念:
输出不仅取决于当时的输入值,而且还与电路过去的状态有关
时序电路的结构特点
![]()
上图是时序电路的一般化模型,由此我们可以总结出时序电路的两大特点:
-
电路由组合电路和存储电路组成( 存储电路由锁存器、触发器构成)
-
电路存在反馈
时序电路的分类
按照时钟的数量,我们可以将时序电路分为同步时序电路和异步时序电路
同时我们还可以依据输出是否与输入有关,将其分为穆尔型(Moore) 和米利型(Mearly)
上图是米利型电路的基本模型,其特点是:输出与输出有关。
(所以输出有可能会受到输入信号的扰动)
。
上图是 穆尔型电路的基本模型,其特点是:输出与输入无关。
时序电路的分析方法
简单总结有三步:
- 写方程
- 画状态转移真值表和输出波形
- 画状态转移图
写方程
看到一副简单的时序电路图,我们需要会看图列写出三个方程:
- 激励方程
用于表达激励信号与输入信号、状态变量的关系式
是不是 感觉有些晦涩难懂?其实这个方程很好列写,我们来看一个例子:
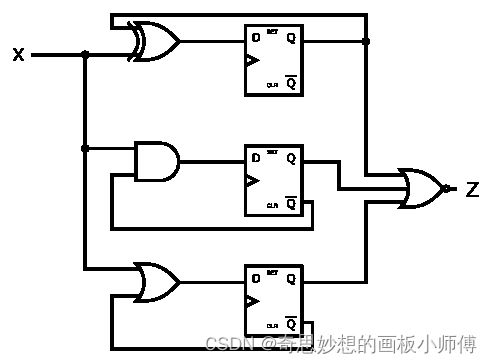
这是HDLBits上的一道题目,为了讲的更加清楚,我们将三个D触发器的输入和输出分别命名为D1~D3,Q1~Q3。
那么什么叫激励呢?所谓激励信号其实就是存储电路(触发器,锁存器)的输入信号,对应D触发器就是我们的“D”端,如果是JK触发器,那么就是J和K端,写激励方程其实就是写出 激励信号的逻辑表达式。
看图,我们能很快写出,D1 = Q1^X、D2 =(!Q2)&(X) ,D3 = (!Q3)|X;这就是所谓激励方程。
2.状态方程
状态方程说实话是三个方程中最需要前面记忆和积累的一个方程,因为它的列写和选用的触发器和锁存器有关系。那怎么样开始列写呢?
首先,我们要明确,状态方程是在触发沿来临时,描述触发器输入和输出的方程。
例如D触发器,这个方程就应该列写为:
我们通常将其写成 次态![]() 与 输入变量A 和 现态
与 输入变量A 和 现态![]() 的关系。
的关系。
例子:
其状态方程可以写成:
3.输出方程
输出方程很好写,主要是表达输出信号与输入信号、状态变量的关系式。上面的例子中,输出方程:
需要注意的是,输出往往都是组合逻辑,所以,输出方程中的状态变量是 现态。
画状态转移真值表和状态波形
为什么要画状态转移真值表或者状态转移波形?我个人认为是为了将抽象的电路具体化。试想,没有人喜欢看着一堆杂乱的布线和若隐若现的几个逻辑器件分析电路的功能,虽然论易懂性,,状态转移图比状态转移真值表更加易懂,但是画状态转移图需要先画出状态转移真值表。
状态转移真值表,顾名思义,其中必须要包含现态,输入,次态和输出,这四个变量。一般我们将状态转移真值表化成这样:
或者我们干脆写出状态表的形式:
这边的重点就是对于图表格式的记忆,我们试着解读一下第一行的内容:
当现态为00时,若输入A为0,那么相应次态为00,输出为0;若输出A为1,那么次态为10,输出为0;
状态波形可以由状态转移真值表轻松画出,但是波形图在手工分析中不常用,绘制难度也不大,只需要将时钟信号的上升沿或者下降沿进行信号变换即可。
状态转移图
状态转移图是描述一个状态机最直观的方法,用上面的例子画出状态转移图:
很容易知道,状态转移图的最基本结构就是下面这个小单元,Q1Q0是状态,A是相应状态转换的输入,Y是时序电路的输出,这是一个米利型电路的状态图,一般穆尔型电路的Y可以画在圆圈里,和状态用 / 隔开。
状态转移图可以用于直观分析时序电路系统的功能,例如计数器,移位寄存器,以及电路是否可以自启动,以及有效状态的个数等等。
路漫漫其修远兮,吾将上下而求索。