Pytorch学习进度记录

Tensor创建

直接创建

torch.tensor()

功能： 从data创建tensor

• data: 数据，可以是list, numpy
• dtype: 数据类型，默认与data一致
• device: 所在设备，cuda/cpu
• requires_grad: 是否需要梯度
• pin_memory: 是否存于锁页内存

torch.tensor(
	data,
    dtype = None,
    device = None,
    requires_grad = False;
    pin_memory = False)

#方法一：
arr = np.ones((3, 3))
t = torch.tensor(arr, device='cuda')

功能： 从numpy创建tensor

注意事项： 从torch.from_numpy创建的tensor与原ndarray共享内存，当修改其中一个的数据，另一个也将被改动

#方法二：
arr = np.array([[1, 2, 3], [4, 5, 6]])
t = torch.from_numpy(arr)

依据数值创建

torch.zeros()

功能： 依size创建全 0 张量

• size: 张量的形状，如 (3, 3)、(3, 244, 244 )
• out: 输出的张量
• layout: 内存中布局形式，有 strided, sparse_coo等
• device: 所在设别
• requires_grad: 是否需要梯度

out_t = torch.tensor([1])
t = torch.zeros((3, 3), out = out_t)
print(id(t), id(out_t), id(t) == id(out_t))
#1910503281032 1910503281032 True

由上可知道， out 的实际功能就是将 torch.zeors 生成的张量赋值给 out_t 包括地址

torch.zeors_like()

功能： 依input形状创建全0张量

torch.zeors_like(
	input,
    dtype=None,
    layout=None,
    device=None,
    requires_grad=False
)

torch.ones()

torch.ones_like()

torch.full()

torch.full(
	size,
    fill_value,
    out=None
    dtype=None,
    layout=torch.strided,
    device=None,
    requires_grad=False
)

torch.full((3, 3), 10)

torch.arange()

功能： 创建等差的 1 维张量

注意事项： 数值区间为 [start, end)

torch.arange(start=0,
            end,
            step=1,
            out=None,
            dtype=None,
            layout=torch.strided,
            device=None,
            requires_grad=False)

torch.arange(2, 10 ,2)

torch.linspace()

功能： 创建均分的 1 维张量

注意事项： 数值区间为 [start, end]

• steps: 数列的长度

torch.arange(start,
            end,
            step=100,
            out=None,
            dtype=None,
            layout=torch.strided,
            device=None,
            requires_grad=False)

t = torch.linespace(2, 10, 6) #tensor([ 2.0000, 3.6000, 5.2000, 6.8000, 10.0000 ])

依概率分布创建张量

torch.normal()

功能： 生成正态分布(高斯分布)

• mean: 均值
• std: 标准差

torch.normal(mean, std, out=None)

torch.normal(mean, std, size, out=None)

当都是标量的时候，需要添加size

四种模式：

• mean为标量， std为标量
• mean为标量， std为张量
• mean为张量， std为标量
• mean为张量， std为张量

torch.randn()

torch.randn_like()

功能： 生成标准正态分布

拼接、切分、索引和变换

一、张量拼接与切分

cat()不会扩张张量纬度， 而stack()会扩张张量的纬度

1.1 torch.cat()

• tensors: 张量序列
• dim: 要拼接的纬度

torch.cat(tensors, dim=0, out=None)

t = torch.ones((2, 3))
t_cat = torch.cat([t, t], dim=0) #([4, 3])
# t_cat = torc.cat([t, t, t], dim=1) #([2, 9])

1.2 torch.stack()

• tensors: 张量序列
• dim: 要拼接的纬度

torch.stack(tensors, dim=0, out=None)

t = torch.ones((2, 3))
t_stack = torch.stack([t, t], dim=2) #([2, 3, 2])
#t_stack = torch.stack([t, t], dim=0) #([2, 2, 3])
#t_stack = torch.stack([t, t, t], dim=0) #([3, 2, 3])

1.3 torch.chunk()

功能： 将张量按纬度dim进行平均切分

返回值: 张量列表

注意事项： 若不能整除，最后一份张量小于其他张量

• input: 要切分的张量
• chunks: 要切分的份数
• dim: 要切分的纬度

torch.chunk(input, chunks, dim=0)

a = torch.ones((2, 5))
list_of_tensors = torch.chunk(a, dim=1, chunks=2)
for idx, t in enumerate(list_of_tensors):
    print("第{}个张量：{}, shape is {}".format(idx+1, t , t.shape))
'''
第1个张量： tensor([[1., 1., 1.],
        [1., 1., 1.]]), shape is torch.Size([2, 3])
第2个张量： tensor([[1., 1.],
        [1., 1.]]), shape is torch.Size([2, 2])
'''

torch.split()

功能： 将张量按纬度 dim 进行切分

返回值： 张量列表

• tensor: 要切分的张量
• split_size_or_sections: 为 int 时，表示每一份的长度；为list时，按list元素切分
• dim: 要切分的纬度

torch.split(tensor, split_size_or_sections, dim=0)

t = torch.ones((2, 5))
list_of_tensors = torch.split(t, [2, 1, 2], dim=1)
#第一个张量shape is torch.size([2, 2]) following: size([2, 1]), size([2, 2])

二、张量索引

2.1 torch.index_select()

功能： 在纬度 dim 上，按 index 索引数据

返回值： 依 index 索引数据拼接的张量

• input: 要索引的张量
• dim: 要索引的纬度
• index: 要索引数据的序号

torch.index_select(input, dim, index, out=None)

t = torch.randint(0, 9, size=(3, 3))
idx = torch.tensor([0, 2], dtype=torch.long)
t_select = torch.index_select(t, dim=1, index=idx)
print("t:\n{}\nt_select:\n{}".format(t, t_select))
'''
t:
tensor([[1, 3, 4],
        [8, 2, 0],
        [8, 1, 4]])
t_select:
tensor([[1, 4],
        [8, 0],
        [8, 4]])
'''

三、张量变换

torch.reshape()

功能： 变换张量形状

注意事项： 当张量在内存中时连续时，新张量与 input 共享数据内存

torch.reshape(input, shape)

torch.transpose()

功能： 交换张量的两个纬度

torch.t(input)

功能： 2维张量转置，对矩阵而言，等价于 torch.transpose(input, 0, 1)

torch.squeeze()

功能： 压缩长度为1的纬度(轴)

• dim: 若为None，移除所有长度为1的轴；若指定纬度，当且仅当该轴长度为1时，可以被移除

torch.squeeze(input, dim=None, out=None)

torch.unsqueeze()

功能： 依据 dim 扩展纬度

• dim: 扩展的纬度

torch.unsqueeze(input, dim, out=None)

线性回归

import torch
import numpy as np
import matplotlib.pyplot as plt

torch.manual_seed(10) #随机数种子
lr = 0.1 #设置学习率

#创建训练数据
x = torch.rand(20, 1) * 10 # x data (tensor), shape = (20, 1)
y = 2 * x + (5 + torch.randn(20, 1)) #y data (tensor), shape = (20, 1)

#初始化参数
w = torch.randn((1), requires_grad=True)
b = torch.randn((1), requires_grad=True)

for iteration in range(1000):
    #前向传播
    wx = torch.mul(w, x)
    y_pred = torch.add(wx, b)

    #计算 MSE LOSS
    loss = (0.5 * (y - y_pred) ** 2).mean()

    #反向传播
    loss.backward()

    #更新参数
    b.data.sub_(lr * b.grad)
    w.data.sub_(lr * w.grad)

    #绘图
    if iteration % 20 == 0:
        plt.scatter(x.data.numpy(), y.data.numpy())
        plt.plot(x.data.numpy(), y_pred.data.numpy(), 'r-', lw=5)
        plt.text(2, 20, 'Loss-%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color': 'red'})
        plt.xlim(1.5, 10)
        plt.ylim(8, 28)
        plt.title("Iteration: {}\nw: {} b: {}".format(iteration, w.data.numpy(), b.data.numpy()))
        plt.pause(0.5)

        if loss.data.numpy() < 1:
            break

计算图

计算图使用来描述运算的有向无环图

计算图有两个主要元素：结点(Node)和边(Edge)

结点表示数据，如向量，矩阵，张量

边表述运算，如加减乘除卷积等

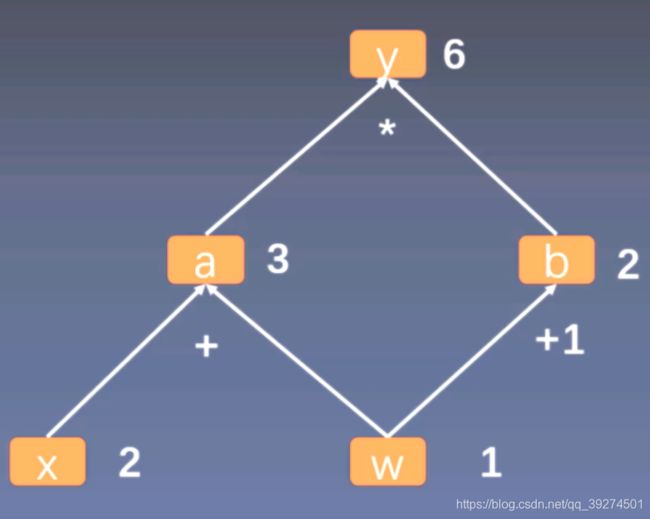
用计算图表示:y = (x + w) * (w + 1)
a = x + w

b = w + 1

y = a * b

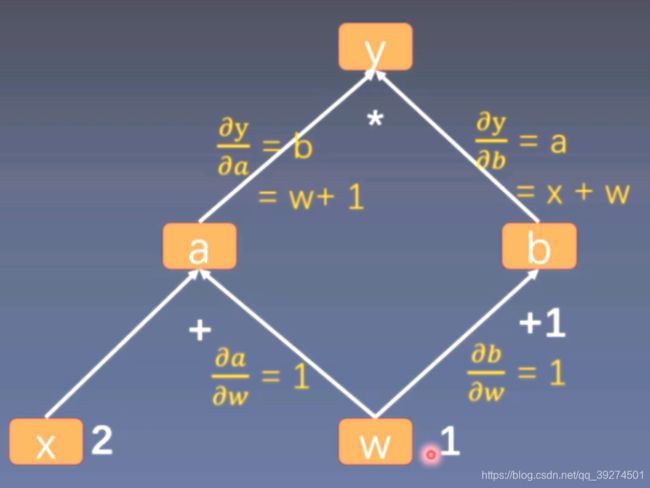
计算图与梯度求导

y = (x + w) * (w + 1)

a = x + w

b = w + 1

y = a * b

$\frac{\partial y}{\partial w}=\frac{\partial y}{\partial a}\frac{\partial a}{\partial w}+\frac{\partial y}{\partial b}\frac{\partial b}{\partial w}$
== b * 1 + a * 1
== b + a
== (w + 1) + (x + w)
== 2 * w + x +1
== 2 * 1 + 2 + 1 = 5