数学建模-相关性分析及热力图

目录

一、相关性分析

二、相关性分析实例

三、三种相关系数

3.1 Pearson线性相关系数 

3.2 Kendall tau系数

3.3 Spearman相关系数

4、Matlab代码

4.1 Pearson 显著性检验

4.2 Pearson 相关系数矩阵

4.3 Kendalltau相关系数矩阵

4.4 Spearman相关系数矩阵 

5、代码部分解释

---

 

一、相关性分析

       相关性分析是指对两个或多个具备相关性的变量元素进行分析，从而衡量两个变量因素的相关密切程度。相关性的元素之间需要存在一定的联系或者概率才可以进行相关性分析。相关性分析是很常用的方法。本文介绍三种相关系数，分别是Pearson相关系数（皮尔逊相关系数），Kendall tau 相关系数（肯德尔相关性系数），Spearman rho相关系数（斯皮尔曼秩相关性系数），同时介绍画相关性系数图和显著性检验。

二、相关性分析实例

       下表是一个全球各个国家幸福指数统计的数据，里面有幸福指数得分、经济、家庭、自由等指标，分析它们之间的相关性。

三、三种相关系数

3.1 Pearson线性相关系数 

        Pearson 线性相关系数是最常用的线性相关系数。最适用数据的形式：线性数据、连续且符合正态分布、数据间差异不能太大。设有m个对象,n个指标,可以构成数据矩阵 ，假设研究矩阵中第a列和第b列  的相关性,设a,b列的相关系数为

其中m为每列的长度，相关系数的值的范围是从–1到+1。值–1表示完全负相关，而值+1表示完全正相关。值0表示列之间没有相关性。

3.2 Kendall tau系数

 3.3 Spearman相关系数

        适用于两列变量，具有等级变量性质具有线性关系的数据，能够很好处理序列中相同值和异常值。Spearman 等效于应用于和列的秩序的 Pearson 线性相关系数。对于第a列和第b列的相关性,设a,b列的相关系数为

其中d为两个列的秩之差，m为每列的长度。

4、Matlab代码

4.1 Pearson 显著性检验

clc;clear;
load('happydata.mat')
%相关性分析
%默认类型为Pearson系数
[xiangguan,p_value]=corr(data);%等效于xiangguan=corr(data,'Type','Pearson');
%x轴和y轴的标签，要和数据的列数对应
index_name={'Score','Economy','Family','Health','Freedom','Generosity','Trust','Residual'};
y_index = index_name;
x_index=index_name;
figure(1)
%字号12，字体宋体，可以随意改变 显示默认配色
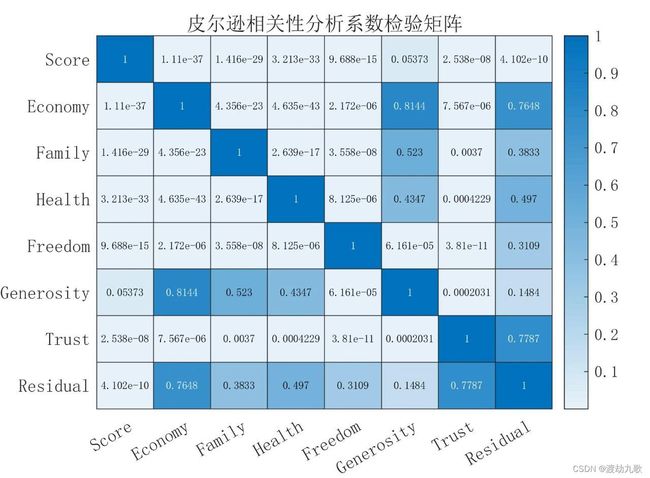
H = heatmap(x_index,y_index, p_value, 'FontSize',12, 'FontName','宋体');
H.Title = '皮尔逊相关性分析系数检验矩阵';

         P-value矩阵值小于0.05时说明相关性显著，否则不显著。例如：Economy和Freedom的P-value值很小，相关性显著。Economy和Freedom的P-value值为0.84144大于0.05，相关性不显著，说明它们两者基本不相关。

4.2 Pearson 相关系数矩阵

figure(2)
% 可以自己定义颜色块
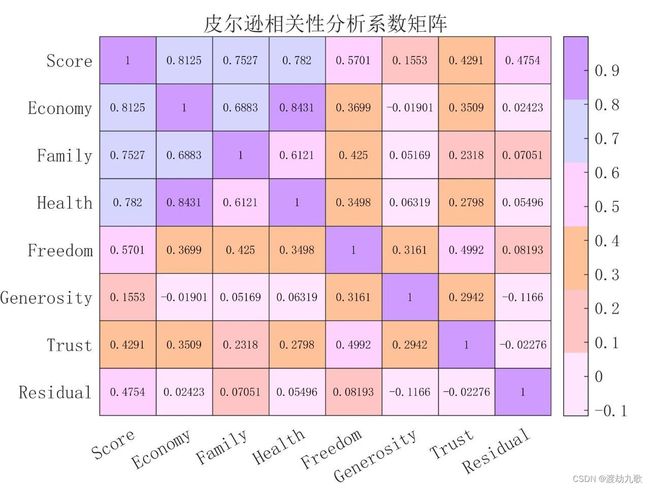
H = heatmap(x_index,y_index, xiangguan, 'FontSize',12, 'FontName','宋体');
H.Title = '皮尔逊相关性分析系数矩阵'; 
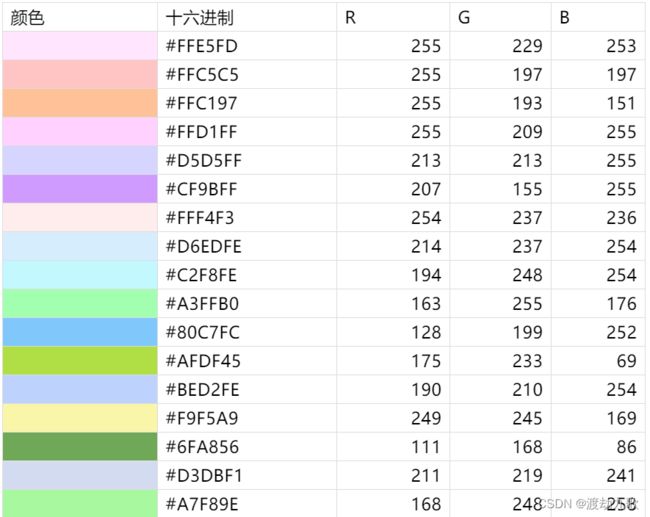
yandata=xlsread('颜色图.xlsx');
yandata1=yandata(1:6,:);% 取颜色表的1—6行颜色
color=yandata1/255;
colormap(color)

 

 我们可以自定义热力图的颜色，默认热力图颜色是第一张图的蓝色系。建议可以把自己喜欢的颜色保存到一张表里方便以后画图配色，在此导入了一张颜色的表：

 

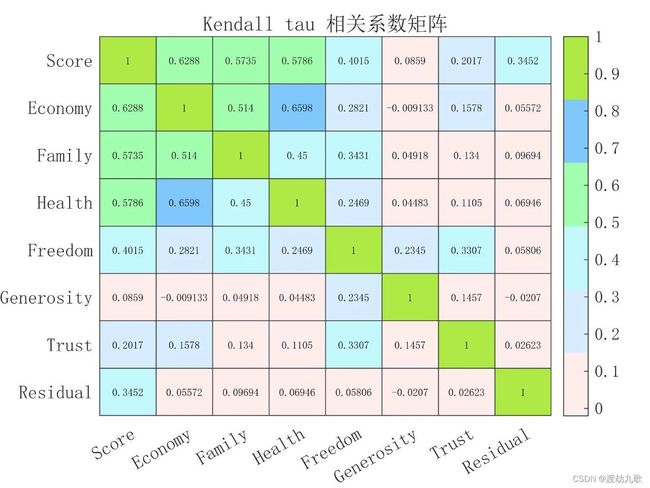
 4.3 Kendalltau相关系数矩阵

%  Kendall tau 系数
figure(3)
[xiangguan,~]=corr(data,'Type','Kendall');
H = heatmap(x_index,y_index, xiangguan, 'FontSize',12, 'FontName','宋体');
H.Title = 'Kendall tau 相关系数矩阵'; 
% 自己定义颜色块
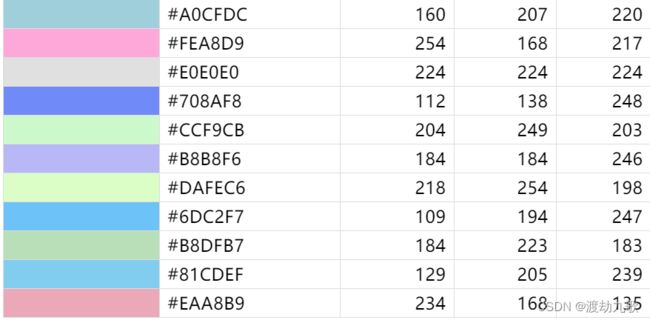
yandata=xlsread('颜色图.xlsx');
yandata1=yandata(7:12,:);% 取7—12行颜色
color=yandata1/255;
colormap(color)

4.4 Spearman相关系数矩阵 

%Spearman系数
figure(4)
[xiangguan,~]=corr(data,'Type','Spearman');
H = heatmap(x_index,y_index, xiangguan, 'FontSize',12, 'FontName','宋体');
H.Title = 'Spearman相关系数矩阵'; 
% 自己定义颜色块
yandata=xlsread('颜色图.xlsx');
yandata1=yandata([8,9,5,23,21],:);% 取指定行颜色
color=yandata1/255;
colormap(color)

5、代码部分解释

1、heatmap(tbl,xvar,yvar) 基于表 tbl 创建一个热图。xvar 输入参数指示沿 x 轴显示的表变量。yvar 输入参数指示沿 y 轴显示的表变量。默认颜色基于计数聚合，这种方法计算每对 x 和 y 值一起出现在表中的总次数。

2、heatmap(tbl,xvar,yvar,'ColorVariable',cvar) 使用 cvar 指定的表变量来计算颜色数据。默认的计算方法为均值聚合。

3、heatmap(cdata) 基于矩阵 cdata 创建一个热图。热图上的每个单元格对应 cdata 中的一个值。使用行向量 r 指定重复方案。例如，repmat(A,[2 3]) 与 repmat(A,2,3) 返回相同的结果。

4、heatmap(xvalues,yvalues,cdata) 指定沿 x 轴和 y 轴显示的值的标签。