【算法】二分相关题目

二分相关

二分查找

https://leetcode.cn/problems/binary-search/

在一个有序数组当中，查找值为target的元素，返回下标

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0,right = nums.size()-1;
        //当二者指向同一个元素的时候也要判断
        //例如：nums:[5] target:5 如果写成left < right 那么返回-1是错误的！应该返回的是0
        while(left <= right) 
        {
            int mid = (left + right) / 2;
            if(nums[mid] > target)
                right = mid - 1; //去左侧找
            else if(nums[mid] < target)
                left = mid + 1; //去右侧找
            else 
                return mid;
        }   
        return -1;
    }
};

---

在排序数组中查找元素的第一个和最后一个位置

https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置

• 本质是：在有序数组当中，找>=某个数最左侧的位置，找<=某个数最右侧的位置
• 但是这里要求必须要找到严格等的位置

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        int n = nums.size();
        vector<int> ans;
        if(n == 0) return {-1,-1};
        //1.找>=tarhet元素的最左边位置
        int left = 0,right = n-1;
        int index = 0;//记录位置
        while(left <= right)
        {
            int mid = (left + right) / 2;
            if(nums[mid] >= target)
            {
                index = mid;
                right = mid -1; //去左侧找更接近的
            }
            else 
                left = mid + 1;
        }
        //判断数组是否存在值为target的元素
        if(nums[index] != target) return {-1,-1};
        
        ans.push_back(index);

        //2.找<=target元素的最右边位置
        left = 0,right = n - 1;
        while(left <= right)
        {
            int mid = (left + right) / 2;
            if(nums[mid] <= target)
            {
                index = mid;
                left = mid +1;//去右侧找更接近的答案
            }
            else 
                right = mid - 1;
        }
        ans.push_back(index);
        return ans;
    }
};

---

寻找峰值

https://www.nowcoder.com/practice/fcf87540c4f347bcb4cf720b5b350c76?tpId=295&tqId=2227748&ru=/exam/company&qru=/ta/format-top101/question-ranking&sourceUrl=%2Fexam%2Fcompany

给定一个长度为n的数组nums，请你找到峰值并返回其索引。数组可能包含多个峰值，在这种情况下，返回任何一个所在位置即可。

1.峰值元素是指其值严格大于左右相邻值的元素。严格大于即不能有等于

2.假设 nums[-1] = nums[n] = $-\infty$

3.对于所有有效的 i 都有 nums[i] != nums[i + 1]

---

方法1：直接遍历数组，如果当前元素比周围两个元素都大，说明当前元素就是峰值元素

int findPeakElement(vector<int>& nums) 
{
    //特判第一个元素和最后一个元素
    int n = nums.size();
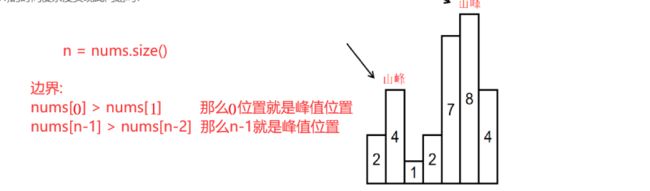
    if(nums[0] > nums[1]) return 0;
    if(nums[n-1] > nums[n-2]) return n - 1;
    //判断[1,n-2]位置的元素,看哪个位置的元素满足比周围元素都大
    for(int i = 1;i<=n-2;i++)
    {
        if(nums[i] > nums[i-1] && nums[i] > nums[i+1])
            return i;
    }
    return -1;
}

---

方法2：二分查找

只要出现 /\这种形式，就是峰值，如果中间位置不是峰值，那么肯定有一边的值比中间位置的值大

int findPeakElement(vector<int>& nums) {
    //特判第一个元素和最后一个元素
    int n = nums.size();
    if (nums[0] > nums[1]) return 0;
    if (nums[n - 1] > nums[n - 2]) return n - 1;
    //在[1,n-2]范围上进行二分
    int left = 1,right = n-2;
    while(left <= right)
    {
        int mid = (left + right)  /2;
        if(nums[mid] < nums[mid+1]) //从mid到mid+1呈现上升趋势(/)
        {
            left = mid + 1;//去右边找下降(\)趋势,就能找到峰值
        }
        else if(nums[mid] < nums[mid-1]) //mid-1到mid呈现下降趋势(\)
        {
            right = mid - 1;//去左边找上升(/)趋势,就能找到峰值
        }
        else  //nums[mid] > nums[mid+1] && nums[mid] > nums[mid-1]
            return mid;
    }
    return -1;
}

---

x 的平方根

https://leetcode.cn/problems/sqrtx/

方法1：暴力求解：枚举$[0,x]$的所有数进行判断

class Solution {
    public:
    int mySqrt(int x) {
        // 由于两个较⼤的数相乘可能会超过 int 最⼤范围  因此⽤ long long
        long long i = 0;
        for (i = 0; i <= x; i++)
        {
            // 如果两个数相乘正好等于 x，直接返回 i
            if (i * i == x) return i;
            // 如果第⼀次出现两个数相乘⼤于 x，说明结果是前⼀个数
            if (i * i > x) return i - 1;
        }
        // 为了处理oj题需要控制所有路径都有返回值
        return -1;
    }
};

---

方法2：使用二分。用long是为了防止mid*mid过大导致溢出！当然也可以将判断条件写成下面这种: $if(mid\ast mid>x)等价于=>if(mid>(x/mid))$

class Solution {
public:
    int mySqrt(int x) {
        //二分法
        if(x == 0)    return 0;
        if(x<=3) return 1;
        //在[1,x]范围进行二分
        long left = 1;
        long right = x;
        long ans = 1;//记录答案
        while(left <= right)//当left和right指向同一个数也需要判断
        {
            long mid = left +(right - left)/2;
            if(mid*mid > x)
            {
                //去左边二分
                right = mid-1;
            }
            else
            {
                //记录答案,继续去右边查找
                left = mid+1;
                ans = mid;
            }
        }
        return (int)ans;
    }
};

---

0~n-1中缺失的数字

https://leetcode.cn/problems/que-shi-de-shu-zi-lcof/description/

一个长度为n-1的递增排序数组中的所有数字都是唯一的，并且每个数字都在范围0～n-1之内。在范围0～n-1内的n个数字中有且只有一个数字不在该数组中，请找出这个数字

输入: [0,1,3]		输出: 2		输入: [0,1,2,3,4,5,6,7,9]		输出: 8

---

因为数组是有序的，方法1：使用哈希表 方法2：直接遍历 方法3：使用位运算 方法 4：高斯求和公式

class Solution {
public:
    //方法1:使用哈希表
    int missingNumber(vector<int>& nums) {
      unordered_map<int,int> um;
      int n = nums.size();
      for(auto& x:nums)  //在哈希表当中做映射
        um[x]++;
      for(int i = 0;i<=n;i++)
      {
        if(um[i] == 0)  //该元素不在哈希表当中存在=>说明是缺失的数字
          return i;
      }
      return -1;
    }
};
//方法2：直接遍历
class Solution {
public:
    int missingNumber(vector<int>& nums) {
      int n = nums.size();
      for(int i = 0;i<n;i++)
      {
        //数组是有序的
        if(nums[i] != i) return i;  
      }
      return n;//说明缺失的元素是n
    }
};
//方法3：位运算
class Solution {
public:
    int missingNumber(vector<int>& nums) {
      int n = nums.size();
      int miss = 0;
      for(auto& x:nums) miss ^= x; //先和原数组的所有元素进行以异或
      for(int i = 0;i<=n;i++) miss ^= i; //和[0,n]范围上的数进行异或
      return miss;
    }
};

//方法4：高斯求和公式
class Solution {
public:
    int missingNumber(vector<int>& nums) {
      //高斯求和公式：和= (首项+末项)x项数÷2
      int n = nums.size();
      int total = (0+n) * (n+1) / 2; 
      int sum = 0;
      for(auto& x:nums) sum+=x;
      return total - sum;//缺失的数
    }
};

方法5：二分算法

因为数组是升序排列的：

• 在第⼀个缺失位置的左边，数组内的元素都是与数组的下标相等的
• 在第⼀个缺失位置的右边，数组内的元素与数组下标是不相等

可以利⽤这个「⼆段性」，来使⽤「⼆分查找」算法

• 如果当前$nums[mid]==mid$ ：说明当前是在左边，要去右边找答案$left=mid+1$
• 如果当前$nums[mid]!=mid$ ：说明当前在右边，要去左边找答案$right=mid$

最后：当跳出循环的时候，还要判断此时指向的值和数组当中的值是否相同，如果相同，那么说明缺失的是下一个数

class Solution {
public:
    int missingNumber(vector<int>& nums) {
      int left = 0,right = nums.size()-1;
      while(left < right) //如果取等,可能会造成死循环 
      {
          int mid = (left + right) / 2;
          if(nums[mid] == mid)
            left = mid + 1;
          else 
            right = mid;
      }
      return left == nums[left] ? left + 1 : left;
    }
};

---

## 搜索插入位置

https://leetcode.cn/problems/search-insert-position/description/

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置

输入: nums = [1,3,5,6], target = 5		输出: 2
输入: nums = [1,3,5,6], target = 2		输出: 1    

---

插入位置的特点：第一次出现比它大的数的前一个位置 || 数组的最后一个位置 =>转化为找到$>=$target的左端点即可

• 直到我们的查找区间的⻓度变为1，也就是当$left == right $的时候，此时$left 或者 right$所在的位置就是我们要找的结果

细节：当跳出循环的时候，要判断当前$left(right)$位置的数和$target$的关系，来判断到底是插入到$left(right)$位置，还是最后一个位置

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
      int left = 0,right = nums.size()-1;
      int ans = 0;
      //找到>=target的最左边位置
      while(left < right)
      {
        int mid = (left + right) / 2;
        if(nums[mid] >= target)
          right = mid;
        else 
          left = mid + 1;
      }
      //如果nums[left] < target 说明应该插入到最后一个位置的后面
      if(nums[left] < target) return left+1;
      else return left;
    }
};

---