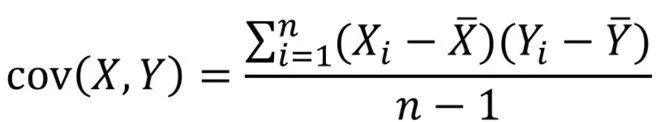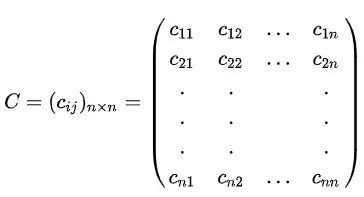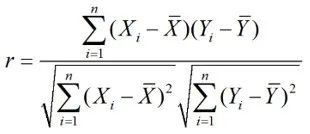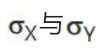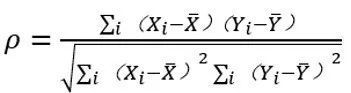相关性分析原理与实操
在数据分析过程中,通常引入统计学名词“变量”来代替不同的影响因素。在大量的变量关系中,相关关系是非常重要的关系。相关关系是指两个变量或若干变量之间存在的一种非严格的确定性关系。例如,土壤是植物养分元素的主要来源之一,则叶片养分元素含量与土壤有效养分元素含量之间可能存在相关关系;生物因环境的变化而改变,在不同纬度地区水热条件存在差异,则植被类型与纬度可能存在相关关系。在数据分析中,这种不确定的关系通常是我们研究的重点。
一、相关关系类型
①按相关的程度
按相关的程度不同,可分为完全相关、不相关、不完全相关。完全相关是指当一种现象的数量变化完全由另一种现象的数量变化所确定,在相关图中,表现为所有观察点都落在直线或曲线上,此时,相关关系就转化为函数关系。不完全相关是指两个现象之间的关系介于完全相关和不相关之间,如某国国民收入和国民支出之间的关系。在统计学中,相关分析主要研究不完全相关现象。
②按依存关系的表现形式
按依存关系的表现形式不同,可分为线性相关、非线性相关。线性相关是指两种相关现象之间的关系近似地表现为一条直线。非线性相关是指当一个变量发生变动时,另一个变量的变动在数值上不是均等的,在相关图中,二者之间形成的坐标点的分布趋势呈曲线形态,如二次抛物线、指数曲线、双曲线等。
③按相关的方向
按相关的方向不同,可分为正相关、负相关。正相关是指当一个变量的数值增加(或减少)时,另一个变量的数值也随之增加(或减少),即同方向变化。反之即为负相关。
二、相关分析的方法
①散点图
将X轴和Y轴定义为不同变量,通过观察数据点的分布情况可以清晰直观地确定变量间的相关关系。然而,无法对相关关系进行准确的度量,缺乏说服力,并且当数据超过两组时也无法完成各组数据间的相关分析。
②协方差
协方差用来衡量两个变量的总体误差,如果两个变量的变化趋势一致,协方差就是正值,说明两个变量正相关。如果两个变量的变化趋势相反,协方差就是负值,说明两个变量负相关。如果两个变量相互独立,那么协方差就是0,说明两个变量不相关。当变量为两组时的计算公式:
其中,
为X与Y的样本均值;n为样本数量。
当变量是两组以上的数据时,则需要使用协方差矩阵。矩阵计算公式如下:
其中,c为cov,n为样本数量。以X、Y、Z三个变量为例,c11是cov(X,X),c12是cov(X,Y),c13是cov(X,Z),以此类推。协方差可以通过数字衡量变量间的相关性,但无法对相关的密切程度进行度量。
③相关系数
相关系数(Correlation coefficient)是反应变量之间关系密切程度的统计指标,度量两要素之间的线性关系。相关系数的取值区间在1到-1之间。常见的相关系数有Pearson相关系数、Spearman相关系数和Kendall相关系数等。此外,相关系数分为样本相关系数(r)以及总体相关系数(ρ)。样本相关系数是根据样本数据计算出来的,而总体相关系数是根据总体全部数据计算出来的。
(1) Pearson相关系数
A.定义及解释
两个变量之间的Pearson相关系数定义为这两个变量的协方差与二者标准差积的商,这定义了总体相关系数,用ρ表示:
若用样本计算的协方差和标准差代替总体的协方差和标准差,则为样本相关系数,通常用表示:
另一个与上式等效的公式是通过标准化以后变量均值的积定义的,如下式所示;
其中,cov ( X, Y )为 X 的协方差乘以 Y 的协方差;
为X与Y的标准差;
为X与Y的样本均值;SX与SY为X与Y的样本标准差;n为样本数量。
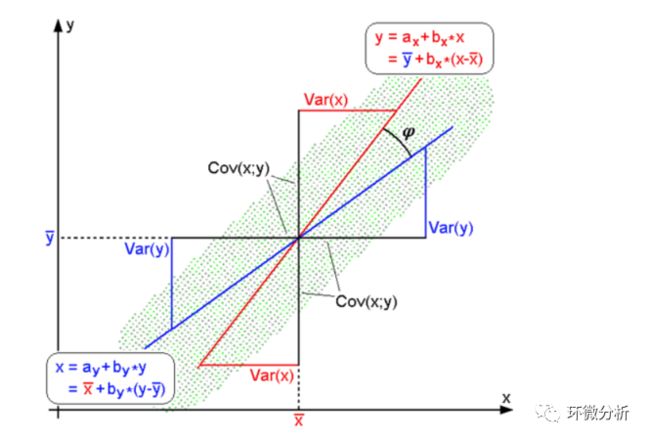
总体或样本Pearson相关系数绝对值均小于或等于1。相关系数绝对值为1时,说明所有数据点均落在同一条直线上(样本),或两变量完全在同一条直线上(总体)。Pearson相关系数具有对称性。此外,Pearson相关系数不随变量的位置或是大小发生变化。对于没有中心化的数据, 相关系数与两条可能的回归线和夹角的余弦值一致(红色为y=gx(x)的回归线,蓝色为x=gy(y) 的回归线)。
B.计算
经过整理后的Pearson相关系数计算公式为:
其中,lxy是X与Y之间的离均差积和;lxx是X的离均差平方和;lyy是Y的离均差平方和。
其中,
为X与Y的样本均值;n为样本数量。
C.适用范围
Pearson相关系数适合做连续变量的相关性分析
(a) 两变量呈直线相关关系,如果是曲线相关可能不准确;
(b) 异常值会对结果造成较大的影响。当使用Pearson相关系数时,需要确定数据是连续变量且成对出现,并且不存在异常值;
(c) 两变量符合正态分布。若是不符合正态分布,可以通过各种手段进行数据转化,例如log()、ln()等。
(2) Spearman相关系数
A.定义及计算
当数据不满足于正态分布,或有一些量无法用数据表达(优秀、良好、合格)时,可以在相关分析中引入秩分(秩分可以理解成等级排序,例如优秀、良好、合格降序排序后用等级1、2、3来代替)。即将两个变量先排序得到相应等级数字,并用等级数字代替原始数据,随后带入到Pearson相关系数公式,得到Spearman相关系数。
将观测的两个变量的对应元素相减得到一个差值d,则还可以将上述公式转化为:
其中:Xi与Yi为两个变量中对应的元素;
为X与Y的样本均值;di为两个变量的对应等级元素相减得到的差值。
等级(秩分)计算示例:
Spearman等级相关是根据等级资料研究两个变量间相关关系的方法。它是依据两列成对等级的各对等级数之差来进行计算的,Spearman等级相关对数据条件的要求没有积差相关系数严格,只要两个变量的观测值是成对的等级评定资料,或者是由连续变量观测资料转化得到的等级资料,不论两个变量的总体分布形态、样本容量的大小如何,都可以用Spearman等级相关来进行研究。如果两个变量之间的相关系数完全相同,斯皮尔曼相关系数就是+1或者-1,换句话说,相关系数距离+1或者-1越近表明两个变量之间的相关性就越强。
B.适用条件
(a) 不服从正态分布;
(b) 总体分布类型未知;
(c) 原始数据使用等级表示。
(3) Kendall相关系数
A.定义及计算
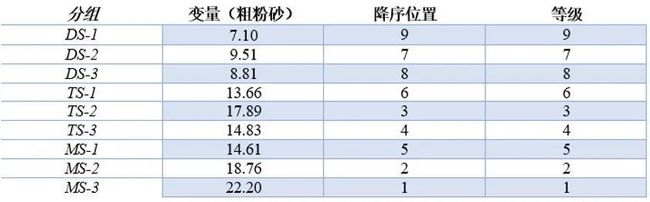
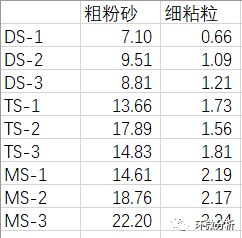
n个同类的统计对象按特定属性排序,其他属性通常是乱序的。同序对(concordant pairs)和异序对(discordant pairs)之差与总对数n(n-1)/2的比值定义为Kendall系数。示例如下图:
其中,MS-3中粗粉砂等级为1,细粘粒等级为1,则细粘粒等级为大于1的组别与MS-1为同序对,共有8个(MS-3/DS-1、MS-3/DS-2、MS-3/DS-3、MS-3/TS-1、MS-3/TS-2、MS-3/TS-3、MS-3/MS-1、MS-3/MS-2)。其余各组别的同序对个数分别为0、1、1、3、3、4、4、6个。则:
总对数SUM=8+7+6+5+4+3+2+1=36
同序对P=0+1+1+3+3+4+4+6+8=30
异序对Q=36-30=6
r=30-6/36=0.667
B.适用条件
适用于两定序变量相关分析,当两定距变量不满足正态分布条件,此时也可使用Kendall's tau_b系数。使用条件和Spearman系数类似,相对而言Spearman系数的更常用一些。
相关系数的优点是可以通过数字对变量的关系进行度量,并且带有方向性,1表示正相关,-1表示负相关,可以对变量关系的强弱进行度量,越靠近0相关性越弱。缺点是无法利用这种关系对数据进行预测,简单的说就是没有对变量间的关系进行提炼和固化,形成模型。
三、实现相关分析的软件
常见的可执行相关性分析的软件有SAS(Statistical Analysis System)、SPSS(Statistical package for the social science )、R、Python、Past和Microsoft Excel等。SAS 与SPSS都是专业的统计程序包,并且具有完备的数据访问、数据管理、数据分析功能模块。作为付费软件,也具有操作方便,统计方法齐全,高效输出等优点。R 语言是为数学研究工作者设计的一种数学编程语言,主要用于统计分析、绘图、数据挖掘。Python作为ABC语言的替代品,能简单有效地面向对象编程,实现多种统计分析。PAST数据分析工具软件是一个简单易用的数据分析工具,具有数据操作,功能策划,生态单变量和多变量统计分析等功能。Excel也可以使用内置公式对小数据集进行相关性分析。
四、相关分析的应用
相关分析应用十分广泛,在医疗、金融、微生物等领域均有应用。例如,可以使用相关分析探究奶茶摄入量与糖尿病病发的联系,也可以利用相关分析探究在同一生境中各种理化条件的相互影响关系。在微生物领域进行数据分析时,通常需要利用相关分析探究理化与ARGs/MGEs、ARGs与MGEs、理化与微生物、微生物与ARGs/MGEs等的联系,来解释微生物演替机理或探究抗性基因潜在宿主菌等。分析结果可通过相关性热图,网图等进行可视化。
五、相关分析示例
①绘制散点图
(1) 导入数据
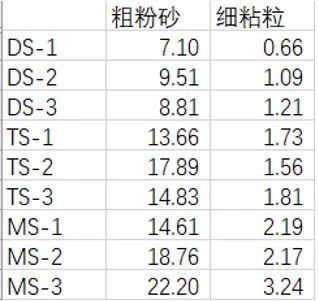
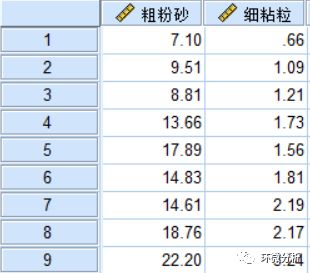
使用Excel将样地的理化数据整理为下图格式。列为理化因子指标,行为处理。数据为不同草地类型中粗粉砂和细粘粒含量,1-3为平行数据;关注“环微分析”公众号,后台回复“相关性分析”即可获取示例数据。
将数据导入SPSS,下图1-3为荒漠草地,4-6为典型草地,7-9为草甸草地;
(2) 绘制散点图检验变量是否存在相关关系
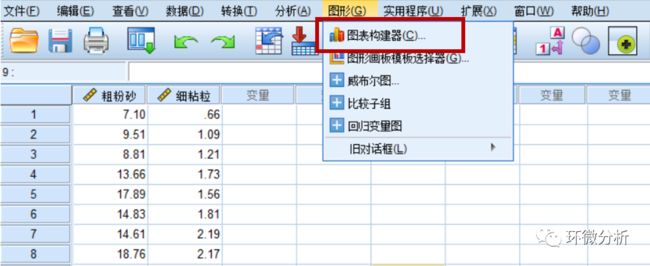
点击图形>图形构建器>图库>散点图/点图>简单散点图,将简单散点图拖到主对话框中,随后将变量分别拖动至X轴和Y轴;
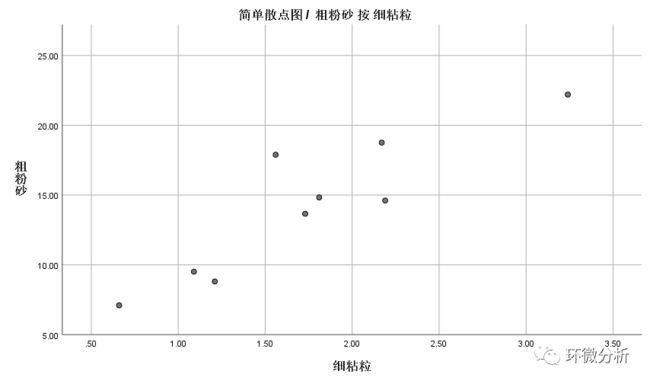
点击确认,得到散点图;
示例数据中,当细粘粒数值增大时,粗粉砂数值也增大,可以看出两变量之间存在正相关关系。
②计算协方差
将细粘粒设为X,粗粉砂设为Y,则:
cov= (7.62 +3.02 +2.83 +0.00 -0.67 +0.05 +0.21 +1.98 +12.07)/8=3.88
协方差为正值,说明粗粉砂和细粘粒成正相关关系。
③使用SPSS计算相关系数
(1) 检验变量间是否存在异常值
异常值是与整体数据分布不同的点,通过观察散点图可以很容易筛选异常值。如果存在异常值,则不适合使用Pearson相关系数。因为异常值会对Pearson造成较大影响。观察上面得到的散点图发现示例数据不存在异常值。但仅通过是否存在异常值不足以确定变量可以使用Pearson相关系数,还应进行正态分布检验。
(2) 正态分布检验
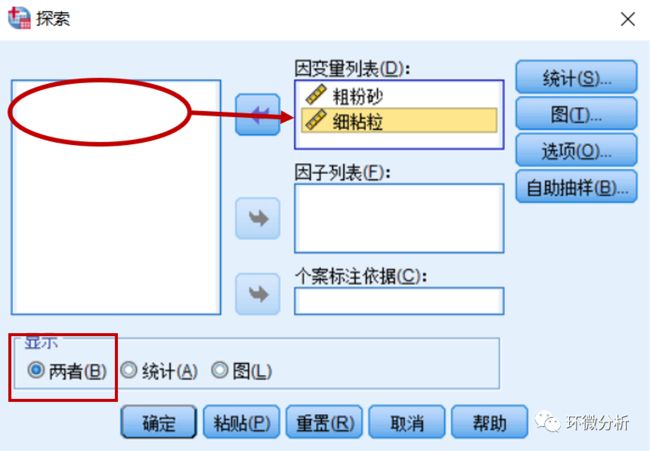
在主页面点击分析>描述统计>探索,将两个变量拖进因变量列表,在显示框中选择两者;
选择右侧图选项,在箱图框中选择无,在描述图框中均不选,在含检验的正态图框中打钩;
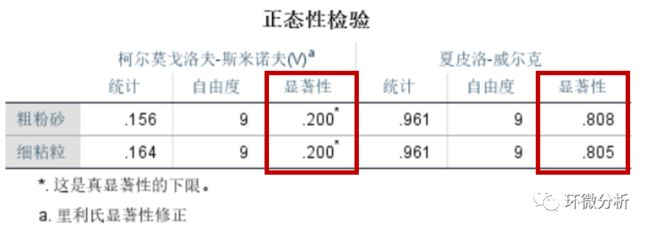
点击确定后,得到正态分布结果:
上图中采用采用的是K-S检验以及Shapiro-Wilk检验的结果。当显著性Sig>0.05时,表明该变量服从正态分布,否则为非正态分布。如表所示,上述数据检验结果显示Sig均大于0.05,说明变量间符合正态分布。三种相关系数均可以使用。
(3) 计算相关系数
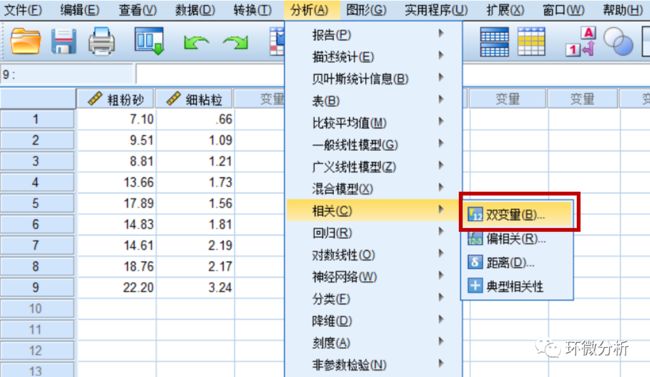
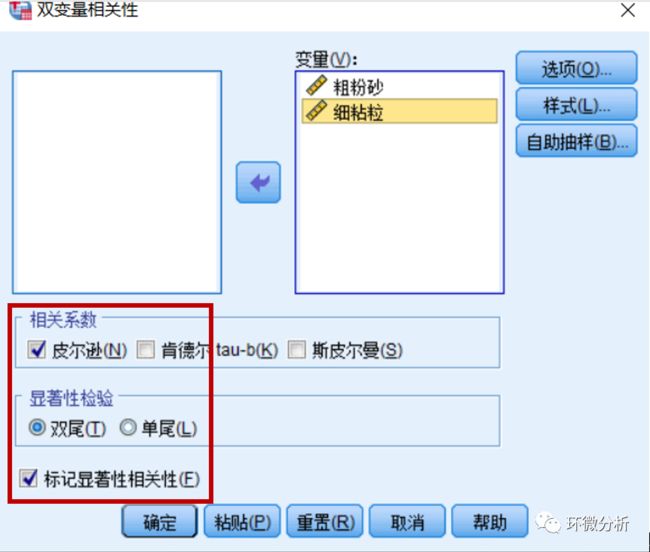
在主页面选择分析>相关>双变量,将两变量拖进变量框中,在相关系数框中选择相关系数计算方法(Pearson、Spearman和Kendall)。首先选择Pearson相关系数计算,点击确认。
得到结果如下图:
得到的数据表有三行,第一行皮尔逊相关性是相关系数r的值。一般情况下,0.8-1.0为极强相关;0.6-0.8为强相关;0.4-0.6为中等程度相关;0.2-0.4为弱相关;0.0-0.2 为极弱相关或无相关。本示例中,Pearson相关系数为0.897,说明粗粉砂和细粘粒之间存在极强的相关关系。
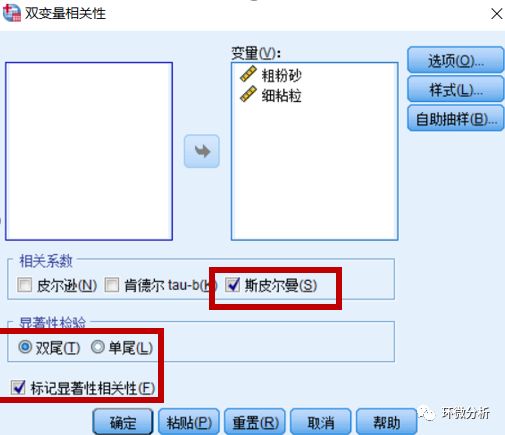
Spearman和Kendall的使用范围更广泛,在相关系数框中选择Spearman或Kendall相关系数,只有相关系数计算方法发生变化,其余设置同Pearson相关系数计算。相关系数计算方法选择Spearman,点击确定;
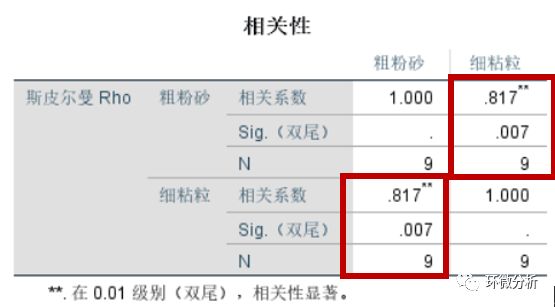
得到结果如下图:
本示例中,Spearman相关系数为0.817,说明粗粉砂和细粘粒存在极强的相关关系。
相关系数计算方法选择Kendall,点击确定;
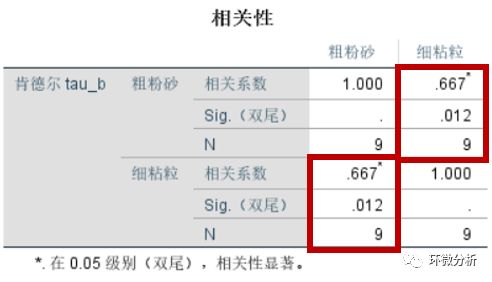
得到结果如下图:
本示例中,Kendall相关系数为0.667,说明粗粉砂和细粘粒存在中等程度相关关系。
(4) 显著性检验
相关系数矩阵表中Sig.(双尾)为显著性检验结果P值。这是因为在数据处理过程中,可能存在抽样的随机性和样本较少等问题,因此相关系数不能直接用来说明两变量之间是否存在显著的线性相关关系,必须进行显著性检验。相关分析的显著性检验,通常使用假设检验的方式对总体的显著性进行推断。一般情况下P<0.05视为显著,P<0.01视为极显著。显著性检验步骤如下:
A.假设两变量无显著线性关系,即两个变量存在零相关;
B.构建新的统计量t,如下式所示:
在变量X与Y服从正态分布时,该t统计量服从自由度为n-2的t分布。计算统计量t,并查询t分布对应的概率P值,如果P<0.05则说明两变量存在显著的线性相关关系,反之则不存在。在上述示例数据中,三种相关系数显著性检验结果为P值均小于0.05,说明粗粉砂和细粘粒存在显著线性关系。
提示:由上述分析可知,三种方法计算出来的相关系数值和显著性检验结果均存在差异,因此在实际应用中应该根据数据特征谨慎选择。当数据不满足双变量正态分布或总体分布未知,或数据资料为定序(有序分类变量)时,适用于Spearman或kendall相关系数。否则,宜用Pearson相关系数。
④使用Excel计算Pearson相关系数
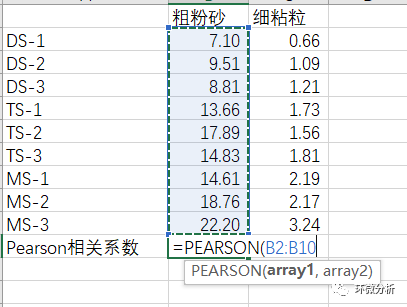
将数据整理成下图格式:
在空白格中输入=PEARSON(),array1选择粗粉砂列数据;
输入逗号,array2列选择细粘粒数据;
单击回车,即可得到相关系数。
六、相关性分析结果可视化
完成相关性分析以后,我们通常将相关性计算结果可视化为热图、网图等图形表达结果。热图、网图等可视化结果能够以更加直观明了的形式展现一个或多个系统中个体之间的相关关系,有助于我们在复杂的关系网络中发现关键节点与重要关系。常用的热图绘图软件(方法)有Excel,Origin,R,Heml以及在线绘图网站;常用的网图绘图软件(方法)有Cytoscape、Gephi以及在线绘图网站。
这篇推文对你有帮助吗?喜欢这篇文章吗?喜欢就不要错过呀,关注本知乎号查看更多的环境微生物生信分析相关文章。亦可以用微信扫描下方二维码关注“环微分析”微信公众号,小编在里面载入了更加完善的学习资料供广大生信分析研究者爱好者参考学习,也希望读者们发现错误后予以指出,小编愿与诸君共同进步!!!
学习环境微生物分析,关注“环微分析”公众号,持续更新,开源免费,敬请关注!
转载自原创文章:
相关性分析原理与实操
最后,再次感谢你阅读本篇文章,真心希望对你有所帮助。感谢!