短期风速预测|LSTM|ELM|批处理(matlab代码)
目录
1 主要内容
LSTM-长短时记忆
ELM-极限学习机
2 部分代码
3 程序结果
4 程序链接
1 主要内容
该程序是预测类的基础性代码,程序对河北某地区的气象数据进行详细统计,程序最终得到pm2.5的预测结果,通过更改数据很容易得到风速预测结果。程序主要分为三部分,分别是基于LSTM算法、基于ELM算法和基于LSTM和批处理组合算法,对于预测类程序,算法组合是创新的方向,很多预测都是通过智能算法对参数寻优+LSTM/ELM等算法进行组合,本次提供的三种基础性代码是对同一数据进行处理分析,并得到相应的预测结果,程序采用matlab编写,无需其他软件包,注释清楚,方便学习!
详实的气象数据是一大亮点。
-
LSTM-长短时记忆
-
ELM-极限学习机
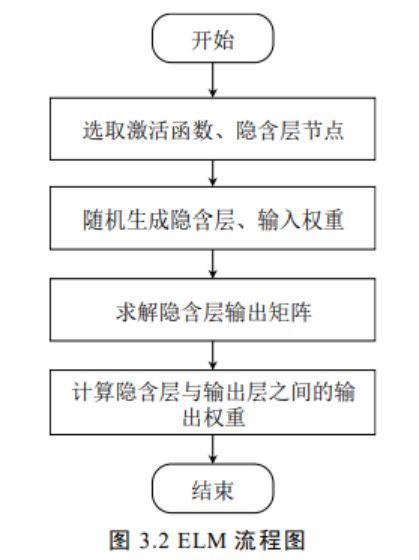
极 限 学 习 机 是 在 原 来 单 隐 含 层 神 经 网 络 (Single-hidden Layer Feedforward Networks,SLFNs)上加以改进后,发展而成的新型智能算法。ELM 方法具有学习效率高的特点,被广泛应用于分类、回归、聚类和特征学习等问题中。作为 一种新型的学习算法,ELM 学习速度快、不容易陷入局部最优,对于单隐层神经网络,可以随机初始化输入权重和偏置并得到相应的输出权重,有效克制了局部 极限的问题。因为极限学习机不包括神经网络反向传播中参数优化的过程,而是 通过求解广义逆矩阵的途径一步求出隐含层的偏置量,这样既提高了算法的精度, 同时收敛速度更快,学习效果更好。
2 部分代码
%% 此程序为不含批训练的lstm
clear;clc;close all;format compact
%% 加载数据
qx1=xlsread('沧州气象日度数据.xlsx','B2:G362');%由于有缺失值,因此只读了前几列最后几列
qx2=xlsread('沧州气象日度数据.xlsx','J2:O362');
qx=[qx1 qx2];
wr=xlsread('沧州污染日度数据.xlsx','C2:C362');%污染数据比气象数据多几条,我把对应日期的数据删除了
input=[wr(1:end-1,:) qx(2:end,:)]';%输入为前一天的pm2.5+预测日的气象 输出为预测日的pm2.5
output=wr(2:end,:)';
input=mapminmax(input,0,1);
[output,outputns]=mapminmax(output,0,1);
%% 提取300个样本为训练样本,剩下样本为预测样本
n=1:size(input,2);
i=300;
train_data=input(:,n(1:i));
train_label=output(:,n(1:i));
P_test=input(:,n(i+1:end));
T_test=output(:,n(i+1:end));
data_length=size(train_data,1);
data_num=size(train_data,2);
%% 网络参数初始化
% 结点数设置
input_num=data_length;%输入层节点
cell_num=3;%隐含层节点
output_num=1;%输出层节点
dropout=0;%dropout系数
cost_gate=1e-10;% 误差要求精度
ab=4*sqrt(6/(cell_num+output_num));% 利用均匀分布进行初始化
% 网络中门的偏置
bias_input_gate=rand(1,cell_num);
bias_forget_gate=rand(1,cell_num);
bias_output_gate=rand(1,cell_num);
%% 网络权重初始化
weight_input_x=rand(input_num,cell_num)/ab;
weight_input_h=rand(output_num,cell_num)/ab;
weight_inputgate_x=rand(input_num,cell_num)/ab;
weight_inputgate_c=rand(cell_num,cell_num)/ab;
weight_forgetgate_x=rand(input_num,cell_num)/ab;
weight_forgetgate_c=rand(cell_num,cell_num)/ab;
weight_outputgate_x=rand(input_num,cell_num)/ab;
weight_outputgate_c=rand(cell_num,cell_num)/ab;
%hidden_output权重
weight_preh_h=rand(cell_num,output_num);
%网络状态初始化
h_state=rand(output_num,data_num);
cell_state=rand(cell_num,data_num);
%% 网络训练学习
for iter=1:100%训练次数
iter
% yita=0.1;
yita=1/(10+sqrt(iter)); %自适应学习率
for m=1:data_num
%前馈部分
if(m==1)
gate=tanh(train_data(:,m)'*weight_input_x);
input_gate_input=train_data(:,m)'*weight_inputgate_x+bias_input_gate;
output_gate_input=train_data(:,m)'*weight_outputgate_x+bias_output_gate;
for n=1:cell_num
input_gate(1,n)=1/(1+exp(-input_gate_input(1,n)));
output_gate(1,n)=1/(1+exp(-output_gate_input(1,n)));
end
forget_gate=zeros(1,cell_num);
forget_gate_input=zeros(1,cell_num);
cell_state(:,m)=(input_gate.*gate)';
else
gate=tanh(train_data(:,m)'*weight_input_x+h_state(:,m-1)'*weight_input_h);
input_gate_input=train_data(:,m)'*weight_inputgate_x+cell_state(:,m-1)'*weight_inputgate_c+bias_input_gate;
forget_gate_input=train_data(:,m)'*weight_forgetgate_x+cell_state(:,m-1)'*weight_forgetgate_c+bias_forget_gate;
output_gate_input=train_data(:,m)'*weight_outputgate_x+cell_state(:,m-1)'*weight_outputgate_c+bias_output_gate;
for n=1:cell_num
input_gate(1,n)=1/(1+exp(-input_gate_input(1,n)));
forget_gate(1,n)=1/(1+exp(-forget_gate_input(1,n)));
output_gate(1,n)=1/(1+exp(-output_gate_input(1,n)));
end
cell_state(:,m)=(input_gate.*gate+cell_state(:,m-1)'.*forget_gate)';
end
pre_h_state=tanh(cell_state(:,m)').*output_gate;
h_state(:,m)=(pre_h_state*weight_preh_h)';
%误差计算
Error=h_state(:,m)-train_label(:,m);
Error_Cost(1,iter)=sum(Error.^2);
if(Error_Cost(1,iter)1;
break;
else %权重更新
3 程序结果
上面三个图是标准LSTM算法得到的预测结果,相对平均误差为0.4828。
上述两个图是LSTM+批处理得到的预测结果,相对平均误差为0.3690,可见增加批处理对于预测精度提成达23.6%。
上述两个图是ELM方法预测结果,相对平均误差为0.4052,较LSTM算法有所提升。
4 程序链接
短期风速预测|LSTM|ELM|批处理