(第十一步) STL: stl_rb_tree容器实现
RB-tree
红黑树的重要性,不言而喻,是一种插入和删除都为 O ( l o g ( N ) ) O(log(N)) O(log(N))的数据结构,具体原理可以看这个:红黑树插入和删除分析
之后程序的编写,和注释红黑树重平衡的情况也是对照上文的情况的,这里就不多做介绍,直接开始程序设计
设计的重点
首先根据侯捷书,所述的迭代器之间的关系图,但是我这里直接放在一起,没有分的很细致,设计迭代器
然后红黑树结构设计,引入了一个header结点,来表示根节点的父节点且为红色
-
当红黑树处于初始状态时,只有
header节点(为红色),它的左右子节点初始状态指向自己 -
当插入节点时,
header的父节点指向根结点,左子节点指向最小的节点,右子节点指向最大的节点 -
当不止一个结点存在时,header->left指向最小值,即最左节点,header->right指向最大值,即最右节点
实现功能
- begin()
- end()
- size()
- empty()
- insert_unique(val); 插入元素不重复
- clear();
- erase(val);
- find(val);
额外补充
红黑树是为后面的set、map准备,需要有键值,所以在Functional.h添加了一个仿函数identity(证同)
//********** [identity] ****************
template<class T>
struct identity {
const T& operator()(const T& x)const { return x; }
};
stl_rb_tree.h
#ifndef _RB_TREE_H_
#define _RB_TREE_H_
#include "../Includes/Allocator.h"
#include "../Includes/Algorithm.h"
#include "../Includes/Construct.h"
#include "../Includes/Iterator.h"
#include "../Includes/Utility.h"
#include "../Includes/Functional.h"
namespace mySTL {
template<class Key, class Value, class KeyOfValue, class Compare>
class rb_tree;
// 结点颜色
typedef bool rbtree_node_color;
const rbtree_node_color rbtree_red = true;
const rbtree_node_color rbtree_black = false;
namespace detail {
// 定义红黑树的结构体
template<class T>
struct rbtree_node
{
typedef rbtree_node_color color_type;
typedef rbtree_node<T>* base_ptr;
T val; // 值
color_type color; // 红黑树颜色
base_ptr parent; // 红黑树非常有必要知道父节点情况
base_ptr left; //
base_ptr right; //
rbtree_node() :val(0),color(rbtree_red), parent(0), left(0), right(0) { }
rbtree_node(const T&val) :val(val), color(rbtree_red), parent(0), left(0), right(0) { }
};
// 迭代器
template<class T>
class rbtree_iterator:public iterator<bidirectional_iterator_tag, T>
{
template<class Key, class Value, class KeyOfValue, class Compare>
friend class rb_tree;
public:
typedef rbtree_iterator<T> iterator;
typedef rbtree_iterator<const T> const_iterator;
typedef ptrdiff_t difference_type;
typedef T value_type;
typedef T* pointer;
typedef T& reference;
typedef bidirectional_iterator_tag iterator_category;
typedef rbtree_node<T> node_type;
typedef rbtree_node<T>* node_ptr;
public:
node_ptr ptr; // 与容器之间的连接
rbtree_iterator(){}
rbtree_iterator(node_ptr p) :ptr(p) {};
rbtree_iterator(const_iterator& x) :ptr(x.ptr) {};
public:
reference operator*()const { return ptr->val; }
pointer operator->()const { return &(ptr->val); }
rbtree_iterator& operator++();
rbtree_iterator operator++(int);
rbtree_iterator& operator--();
rbtree_iterator operator--(int);
template<class T>
friend bool operator==(const rbtree_iterator<T>& lhs, const rbtree_iterator<T>& rhs);
template<class T>
friend bool operator!=(const rbtree_iterator<T>& lhs, const rbtree_iterator<T>& rhs);
private:
// 辅助迭代器函数
// 搜索树的自加 it++
void increment();
// 搜索树的自减 it--
void decrement();
};
}
/* 首先我们应该注意的是模板的参数
* key代表红黑树上存储节点时依据的值
* value即节点的值
* KeyOfValue是仿函数,用于通过value获取到key
* Compare为比较key大小的标准
* Alloc是空间配置器
*/
template<class Key, class Value, class KeyOfValue, class Compare>
class rb_tree
{
private:
friend class detail::rbtree_iterator<Value>;
public:
typedef rbtree_node_color color_type;
typedef ptrdiff_t difference_type;
typedef size_t size_type;
typedef Key key_type;
typedef Value value_type;
typedef value_type* pointer;
typedef value_type& reference;
typedef const value_type* const_pointer;
typedef const value_type& const_reference;
typedef detail::rbtree_node<value_type> rbtreeNode;
typedef rbtreeNode* rbtree_node_ptr;
typedef allocator<detail::rbtree_node<value_type>> rbtreeAllocator;
public:
typedef detail::rbtree_iterator<value_type> iterator;
typedef detail::rbtree_iterator<value_type> const_iterator;
private:
rbtree_node_ptr header;
size_type node_count;
Compare key_compare;
protected:
//construct / destroy / init
rbtree_node_ptr getNode();
rbtree_node_ptr createNode(const Value& val = Value());
void putNode(rbtree_node_ptr ptr);
void deleteNode(rbtree_node_ptr ptr);
void init();
public:
rb_tree(const Compare& comp = Compare());
//复制节点,包括颜色
rbtree_node_ptr clone_node(rbtree_node_ptr x);
~rb_tree();
protected:
// 定义header节点属性
// header的左孩子指向key值最小的节点
rbtree_node_ptr& root()const { return (rbtree_node_ptr&)header->parent; }
rbtree_node_ptr& leftmost() const { return (rbtree_node_ptr&)header->left; }
rbtree_node_ptr& rightmost() const { return (rbtree_node_ptr&)header->right; }
// 使用6个函数,方便获取x的节点成员
static rbtree_node_ptr& left(rbtree_node_ptr x)
{
return (rbtree_node_ptr&)(x->left);
}
static rbtree_node_ptr& right(rbtree_node_ptr x)
{
return (rbtree_node_ptr&)(x->right);
}
static rbtree_node_ptr& parent(rbtree_node_ptr x)
{
return (rbtree_node_ptr&)(x->parent);
}
static reference value(rbtree_node_ptr x)
{
return x->val;
}
static const key_type& key(rbtree_node_ptr x)
{
return KeyOfValue()(value(x));
}
static color_type& color(rbtree_node_ptr x)
{
return (color_type&)(x->color);
}
public:
iterator begin() { return leftmost(); }
//const_iterator begin()const { return const_iterator(leftmost()); }
iterator end() { return header; }
//const_iterator end()const { return const_iterator(header); }
size_type size()const { return node_count; }
size_type max_size() const { return size_type(-1); }
bool empty() const { return node_count == 0; }
public:
pair<iterator, bool> insert_unique(const Value& val); // 插入元素不重复
void clear();
void erase(iterator position);
void erase(const Value& val);
iterator find(const Value& val);
protected:
iterator insert(rbtree_node_ptr x, rbtree_node_ptr p, const Value& val); // 实现插入
void rbtree_rebalance_for_insert(rbtree_node_ptr z, rbtree_node_ptr& root); // 实现插入重平衡
void rbtree_rotate_left(rbtree_node_ptr x, rbtree_node_ptr& root); // 左旋
void rbtree_rotate_right(rbtree_node_ptr x, rbtree_node_ptr& root); // 右旋
void recurErase(rbtree_node_ptr x);
// 删除的重平衡
rbtree_node_ptr rbtree_rebalance_for_erase(rbtree_node_ptr z, rbtree_node_ptr& root);
rbtree_node_ptr findRBTree(const Value& val, bool& isFind);
rbtree_node_ptr RBTreeMinimum(rbtree_node_ptr p);
rbtree_node_ptr RBTreeMaximum(rbtree_node_ptr p);
};
}
#include "../Detail/stl_rb_tree.impl.h"
#endif
stl_rb_tree.impl.h
#ifndef _RB_TREE_IMPL_H_
#define _RB_TREE_IMPL_H_
namespace mySTL {
namespace detail {
// 搜索树的自加 it++
template<class T>
void rbtree_iterator<T>::increment()
{
if (ptr->right != nullptr)
{
// 情况1:存在右节点,后继结点为右子树的最左结点
ptr = ptr->right;
while (ptr->left != nullptr)
ptr = ptr->left;
}
else
{
// 情况2:不存在右节点
node_ptr parent_node = ptr->parent;
// 如果ptr是右节点,向上找出不为右节点的节点
// 如果ptr为最右节点,此时会返回至ptr = root,
while (ptr == parent_node->right)
{
ptr = parent_node;
parent_node = parent_node->parent;
}
// ==出现的特殊情况3:ptr结点为root结点,
// 同时不存在右子树时,header == root->parent == ptr->parent == ptr->right == nullptr
// 为了处理当node为root时并且root无右子树的特殊情况
if (ptr->right != parent_node)
ptr = parent_node;
}
}
// 搜索树的自减 it--
template<class T>
void rbtree_iterator<T>::decrement()
{ // 情况1:ptr指向header时
// 此时是为end(),应该返回最右值,header->right
if (ptr->color == rbtree_red &&
ptr->parent->parent == ptr)
{
ptr = ptr->right;
}
else if (ptr->left != nullptr)
{
// 情况2:存在左节点,前继结点为左子树的最右结点
ptr = ptr->left;
while (ptr->right != nullptr)
ptr = ptr->right;
}
else
{ // 情况3:不存在左节点
node_ptr parent_node = ptr->parent;
// 如果ptr是左节点,向上找出不为左节点的节点
while (ptr == parent_node->left)
{
ptr = parent_node;
parent_node = parent_node->parent;
}
ptr = parent_node;
}
}
template<class T>
inline rbtree_iterator<T>& rbtree_iterator<T>::operator++()
{
increment();
return *this;
}
template<class T>
inline rbtree_iterator<T> rbtree_iterator<T>::operator++(int)
{
auto tmp = *this;
++(*this);
return tmp;
}
template<class T>
inline rbtree_iterator<T>& rbtree_iterator<T>::operator--()
{
decrement();
return *this;
}
template<class T>
inline rbtree_iterator<T> rbtree_iterator<T>::operator--(int)
{
auto tmp = *this;
--(*this);
return tmp;
}
template<class T>
bool operator==(const rbtree_iterator<T>& lhs, const rbtree_iterator<T>& rhs)
{
return lhs.ptr == rhs.ptr;
}
template<class T>
bool operator!=(const rbtree_iterator<T>& lhs, const rbtree_iterator<T>& rhs)
{
return !(lhs == rhs);
}
}
template<class Key, class Value, class KeyOfValue, class Compare>
inline typename rb_tree<Key, Value, KeyOfValue, Compare>::rbtree_node_ptr
rb_tree<Key, Value, KeyOfValue, Compare>::getNode()
{
return rbtreeAllocator::allocate();
}
template<class Key, class Value, class KeyOfValue, class Compare>
inline typename rb_tree<Key, Value, KeyOfValue, Compare>::rbtree_node_ptr
rb_tree<Key, Value, KeyOfValue, Compare>::createNode(const Value& val)
{
rbtree_node_ptr tmp = getNode(); // 开辟空间
mySTL::construct(&(tmp->val), val); // 赋值
return tmp; // 返回指针
}
template<class Key, class Value, class KeyOfValue, class Compare>
inline void rb_tree<Key, Value, KeyOfValue, Compare>::putNode(rbtree_node_ptr ptr)
{
rbtreeAllocator::deallocate(ptr);
}
template<class Key, class Value, class KeyOfValue, class Compare>
inline void rb_tree<Key, Value, KeyOfValue, Compare>::deleteNode(rbtree_node_ptr ptr)
{
mySTL::destroy(&ptr->val);
putNode(ptr);
}
template<class Key, class Value, class KeyOfValue, class Compare>
inline void rb_tree<Key, Value, KeyOfValue, Compare>::init()
{
header = createNode();
leftmost() = header; // 令header左节点为自己
rightmost() = header; // 令header右节点为自己
color(header) = rbtree_red; // 用来区分header和root,在operator--中
root() = nullptr; // header的父节点,红黑树的root为nullptr
// 这里体现一个技巧:插入root结点时,header和root互为对方的父节点
}
/***********************init 结束,开始构造和析构**********************/
template<class Key, class Value, class KeyOfValue, class Compare>
inline rb_tree<Key, Value, KeyOfValue, Compare>::rb_tree(const Compare& comp)
:node_count(0), key_compare(comp)
{
init();
}
template<class Key, class Value, class KeyOfValue, class Compare>
inline typename rb_tree<Key, Value, KeyOfValue, Compare>::rbtree_node_ptr
rb_tree<Key, Value, KeyOfValue, Compare>::clone_node(rbtree_node_ptr x)
{
{
rbtree_node_ptr tmp = createNode(x->val);
tmp->color = x->color;
tmp->left = nullptr;
tmp->right = nullptr;
return tmp;
}
}
template<class Key, class Value, class KeyOfValue, class Compare>
inline rb_tree<Key, Value, KeyOfValue, Compare>::~rb_tree()
{
clear();
putNode(header);
}
/***********************插入的实现**********************/
template<class Key, class Value, class KeyOfValue, class Compare>
inline pair<typename rb_tree<Key, Value, KeyOfValue, Compare>::iterator, bool>
rb_tree<Key, Value, KeyOfValue, Compare>::insert_unique(const Value& val)
{
rbtree_node_ptr p = header; // 根节点的父节点
rbtree_node_ptr x = root(); // 从根节点开始
bool comp = true;
while (x != nullptr) // 从根节点开始往下寻找合适的插入点
{
p = x;
comp = key_compare(KeyOfValue()(val), key(x)); // 对比
x = comp ? left(x) : right(x); // 遇大往左,小往右
}// 离开while循环后,p就为插入点(叶子结点)
// 如果当前x树为空树,直接插入val结点
if (p == header)
{
return pair<iterator, bool>(insert(x, p, val), true);
}
iterator j = iterator(p); // j 指向插入结点的父节点p
if (comp) // comp为真,遇大插左侧
{
if (j == begin()) // 插入为最左结点,即最小结点
{
return pair<iterator, bool>(insert(x, p, val), true);
}
else
{
--j; // 调整j,回头测试
}
}
if (key_compare(key(j.ptr), KeyOfValue()(val))) // 新值不与键值重复,插入
{
return pair<iterator, bool>(insert(x, p, val), true);
}
// 重复,不插入
return pair<iterator, bool>(j, false);
}
template<class Key, class Value, class KeyOfValue, class Compare>
inline typename rb_tree<Key, Value, KeyOfValue, Compare>::iterator
rb_tree<Key, Value, KeyOfValue, Compare>::insert(rbtree_node_ptr x, rbtree_node_ptr p, const Value& val)
{
// x新值插入点,p插入点的父节点,val插入的新值
rbtree_node_ptr z;
if (p == header || key_compare(KeyOfValue()(val), key(p)))
{
z = createNode(val);
left(p) = z;
if (p == header) // p为header时,即当前为空树, leftmost = z;
{
root() = z; // header父节点指向root
rightmost() = z; // header右节点指向z,也就是rightmost = z;
}
else if (p == leftmost()) // 插入结点的父节点为最左结点
{
leftmost() = z; // 维护leftmost(),永远指向最左结点
}
}
else
{ // 树不为空,且comp为false,val小于ptr->val,存放右边
z = createNode(val);
right(p) = z; // 将p的右孩子设置为z
if (rightmost() == p)
{
rightmost() = z; // 维护rightmost(),永远指向最右结点
}
}
// 设定新节点z的父节点、和子节点
parent(z) = p;
left(z) = nullptr;
right(z) = nullptr;
// 重平衡
rbtree_rebalance_for_insert(z, parent(header));
++node_count;
return iterator(z);
}
/***********************插入重平衡**********************/
template<class Key, class Value, class KeyOfValue, class Compare>
inline void rb_tree<Key, Value, KeyOfValue, Compare>::rbtree_rebalance_for_insert(rbtree_node_ptr z, rbtree_node_ptr& root)
{
// z 插入的新节点,root树的根节点
z->color = rbtree_red; // 插入节点必为红色
while (z != root && z->parent->color == rbtree_red)
{
// 情景4:插入结点的父结点为红结点
if (z->parent == z->parent->parent->left)
{
// 情景:插入结点的父亲结点是祖父结点的左子结点
rbtree_node_ptr u = z->parent->parent->right; // 叔叔结点
if (u != nullptr && u->color == rbtree_red)
{
// 情景4.1:叔叔结点存在并且为红结点
u->color = rbtree_black;
z->parent->color = rbtree_black;
z->parent->parent->color = rbtree_red;
z = z->parent->parent; // 更新插入结点,直到更新至root
}
else
{
// 插入情景4.2:叔叔结点不存在或为黑结点,并且插入结点的父亲结点是祖父结点的左子结点
// 插入情景4.2.2:插入结点是其父结点的右子结点,双旋,先P结点左旋,变成情形4.2.1
if (z == z->parent->right)
{
z = z->parent;
rbtree_rotate_left(z, root);
}
// 插入情景4.2.1:插入结点是其父结点的左子结点,单旋,PP结点右旋
z->parent->parent->color = rbtree_red;
z->parent->color = rbtree_black;
rbtree_rotate_right(z->parent->parent, root);
}
}
else
{
// 情景:插入结点的父亲结点是祖父结点的右子结点
// 和4.2处理只是进行对称镜像
rbtree_node_ptr u = z->parent->parent->left;
if (u != 0 && u->color == rbtree_red)
{
// 情景4.1:叔叔结点存在并且为红结点
u->color = rbtree_black;
z->parent->color = rbtree_black;
z->parent->parent->color = rbtree_red;
z = z->parent->parent;
}
else
{
// 插入情景4.3.2:插入结点是其父结点的左子结点,双旋,先P结点右旋,至情景4.3.1
if (z == z->parent->left)
{
z = z->parent;
rbtree_rotate_right(z, root);
}
// 插入情景4.3.1:插入结点是其父结点的右子结点,单旋
z->parent->parent->color = rbtree_red;
z->parent->color = rbtree_black;
rbtree_rotate_left(z->parent->parent, root);
}
}
}
// 情景1,3:直接插入,无需操作即可
root->color = rbtree_black; // 根节点永远为黑
}
/***********************左旋和右旋**********************/
template<class Key, class Value, class KeyOfValue, class Compare>
inline void rb_tree<Key, Value, KeyOfValue, Compare>::rbtree_rotate_left(rbtree_node_ptr x, rbtree_node_ptr& root)
{
// x为旋转节点
rbtree_node_ptr y = x->right;
x->right = y->left;
if (y->left != nullptr)
y->left->parent = x;
// 完成x结点,除x->parent参数的更新
// 开始y节点的更新
y->parent = x->parent;
if (x == root)
{
root = y;
}
else if (x->parent->left == x)
{
x->parent->left = y;
}
else
{
x->parent->right = y;
}
x->parent = y;
y->left = x;
}
template<class Key, class Value, class KeyOfValue, class Compare>
inline void rb_tree<Key, Value, KeyOfValue, Compare>::rbtree_rotate_right(rbtree_node_ptr x, rbtree_node_ptr& root)
{
// 原理同左旋
rbtree_node_ptr y = x->left;
x->left = y->right;
if (y->right != 0)
y->right->parent = x;
y->parent = x->parent;
if (x == root)
{
root = y;
}
else if (x->parent->left == x)
{
x->parent->left = y;
}
else
{
x->parent->right = y;
}
x->parent = y;
y->right = x;
}
// 查找函数
template<class Key, class Value, class KeyOfValue, class Compare>
inline typename rb_tree<Key, Value, KeyOfValue, Compare>::rbtree_node_ptr
rb_tree<Key, Value, KeyOfValue, Compare>::RBTreeMinimum(rbtree_node_ptr p)
{
while (p->left != nullptr)
p = p->left;
return p;
}
template<class Key, class Value, class KeyOfValue, class Compare>
inline typename rb_tree<Key, Value, KeyOfValue, Compare>::rbtree_node_ptr
rb_tree<Key, Value, KeyOfValue, Compare>::RBTreeMaximum(rbtree_node_ptr p)
{
while (p->right != nullptr)
p = p->right;
return p;
}
template<class Key, class Value, class KeyOfValue, class Compare>
inline typename rb_tree<Key, Value, KeyOfValue, Compare>::rbtree_node_ptr
rb_tree<Key, Value, KeyOfValue, Compare>::findRBTree(const Value& val, bool& isFind)
{
rbtree_node_ptr res = parent(header);
isFind = false;
while (res != 0)
{
if (key_compare(KeyOfValue()(val), key(res)))
{
res = left(res);
}
else
{
if (key_compare(key(res), KeyOfValue()(val)))
{
res = right(res);
}
else
{
isFind = true;
break;
}
}
}
return res;
}
template<class Key, class Value, class KeyOfValue, class Compare>
inline typename rb_tree<Key, Value, KeyOfValue, Compare>::iterator
rb_tree<Key, Value, KeyOfValue, Compare>::find(const Value& val)
{
bool isFind = false;
rbtree_node_ptr res = findRBTree(val, isFind);
if (isFind)
{
return iterator(res);
}
else
{
return end();
}
}
// 递归删除值
template<class Key, class Value, class KeyOfValue, class Compare>
inline void rb_tree<Key, Value, KeyOfValue, Compare>::recurErase(rbtree_node_ptr x)
{
if (x != 0)
{
recurErase(left(x));
recurErase(right(x));
deleteNode(x);
}
}
template<class Key, class Value, class KeyOfValue, class Compare>
inline void rb_tree<Key, Value, KeyOfValue, Compare>::clear()
{
recurErase(root());
left(header) = header;
right(header) = header;
parent(header) = nullptr;
}
// 删除
template<class Key, class Value, class KeyOfValue, class Compare>
inline void rb_tree<Key, Value, KeyOfValue, Compare>::erase(iterator position)
{
rbtree_node_ptr to_be_delete = rbtree_rebalance_for_erase(position.ptr, root());
deleteNode(to_be_delete);
--node_count;
}
template<class Key, class Value, class KeyOfValue, class Compare>
inline void rb_tree<Key, Value, KeyOfValue, Compare>::erase(const Value& val)
{
auto positon = find(val);
rbtree_node_ptr to_be_delete = rbtree_rebalance_for_erase(positon.ptr, root());
deleteNode(to_be_delete);
--node_count;
}
// 删除重平衡
template<class Key, class Value, class KeyOfValue, class Compare>
inline typename rb_tree<Key, Value, KeyOfValue, Compare>::rbtree_node_ptr
rb_tree<Key, Value, KeyOfValue, Compare>::rbtree_rebalance_for_erase(rbtree_node_ptr z, rbtree_node_ptr& root)
{ // z删除节点位置
rbtree_node_ptr del_node = z; // 删除的节点
rbtree_node_ptr replace_node = 0; // 替代del_node的节点,真正需要删除的节点
rbtree_node_ptr replace_node_parent; // 删除之后 x 的父节点
// 查找实际需要删除的del_node节点的替换节点replace_node
if (del_node->left == nullptr)
{
// 删除情景1或2:删除结点无子节点或只有一个右子结点
replace_node = del_node->right;
}
else if (del_node->right == nullptr)
{
// 删除情景2:删除结点只有一个左子结点
replace_node = del_node->left;
}
else
{
// 删除情景3:删除结点有两个子结点
// 采用后继结点法,删除节点的右节点的,最左节点
del_node = del_node->right;
while (del_node->left != nullptr)
del_node = del_node->left;
//replace_node = del_node;
replace_node = del_node->right;
}
// 开始我们的大工程,自平衡
// 首先,删除结点值,和替代结点值的交换
if (del_node == z)
{
// 情景1或2,del_node保持不变,== z,步骤如下
// 1.删除结点z的父节点z->parent指向,replace_node替换节点(此时为z的子节点)
// 2.然后替换节点replace_node->parent删除结点z父节点
// 3.保持header->left、header->right的指向,即最小最大的指向,不变
replace_node_parent = del_node->parent;
if (z == root)
{
// 删除结点为根节点
root = replace_node;
}
else if (z == z->parent->left)
{
// 删除结点为父节点的左子结点
z->parent->left = replace_node;
}
else
{
// 删除结点为父节点的右子结点
z->parent->right = replace_node;
}
// 替代结点,代替删除结点
if (replace_node != nullptr) replace_node->parent = z->parent;
if (z == leftmost())
{
// 删除结点为最左节点,更新最左节点,保持最小值
if (z->right == nullptr)
leftmost() = z->parent;
else
leftmost() = RBTreeMinimum(replace_node);
}
if (z == rightmost())
{
// 删除结点为最右节点,更新最右节点,保持最大值
if (z->left == 0)
rightmost() = z->parent;
else
rightmost() = RBTreeMaximum(replace_node);
}
}
else
{
// 情景3,此时del_node != z,del_node == 替换节点位置上
// replace_node = del_node->right;
// 更新del_node左半部分
del_node->left = z->left;
z->left->parent = del_node;
if (z->right != del_node)
{ // 删除结点z的右子结点,有左子结点
// del_node->right 与 del_node->parent之间的更新,即移除del_node结点
replace_node_parent = del_node->parent;
if (replace_node != nullptr)
replace_node->parent = del_node->parent;
del_node->parent->left = replace_node;
// 更新del_node 右半部分
del_node->right = z->right;
z->right->parent = del_node;
}
else
{ // 删除结点z的右子结点,无左子结点
// 此时右半部分保持不变,维持原状即可
replace_node_parent = del_node;
}
// 更新删除结点的父节点
if (z == root)
{
root = del_node;
}
else if (z == z->parent->left)
{
z->parent->left = del_node;
}
else
{
z->parent->right = del_node;
}
del_node->parent = z->parent;
// 完成交换值,并保持删除结点颜色不变,此时删除结点变成删除替换节点
swap(del_node->color, z->color);
// 后面只需要根据颜色进行调整红黑树,所以获取del_node的颜色,即现在的z的颜色
del_node = z;
}
// del_node: 待删节点
// replace_node: 替换del_node的节点,此时replace_node也成为标记节点
// replace_node_parent: replace_node的父节点
// 此时开始调动颜色,如果del_node为红色直接删除即可,为黑色需要分析
// D 待删节点 S 是D的兄弟节点
if (del_node->color == rbtree_black)
{
while (replace_node != root && (replace_node == nullptr || replace_node->color == rbtree_black))
{
// 为双黑色节点
if (replace_node == replace_node_parent->left)
{
// del_node结点是其父结点的左子结点
rbtree_node_ptr s = replace_node_parent->right;
if (s->color == rbtree_red)
{
// 删除情景1.2.2:D结点的兄弟结点S是红结点
s->color = rbtree_black;
replace_node_parent->color = rbtree_red;
rbtree_rotate_left(replace_node_parent, root);
s = replace_node_parent->right;
// 此时变为情景1.2.1.1
}
if ((s->left == nullptr || s->left->color == rbtree_black)
&& (s->right == nullptr || s->right->color == rbtree_black))
{
// 删除情景1.2.1.1:D结点的兄弟结点S的子结点SL 、SR都为黑结点null
s->color = rbtree_red;
// 向上更新
replace_node = replace_node_parent;
replace_node_parent = replace_node_parent->parent;
}
else
{
if (s->right == nullptr || s->right->color == rbtree_black)
{
// 删除情景1.2.1.2:D结点的兄弟结点S的子结点SL为红,SR为黑、null
if (s->left != nullptr)
s->left->color = rbtree_black;
s->right->color = rbtree_red; // 变红后,后就操作了
rbtree_rotate_right(s, root); // 右旋后,近似变为删除情景1.2.1.3,比较抽象
s = replace_node_parent->right;
}
// 删除情景1.2.1.3:D结点的兄弟结点的子结点SL为黑null(或者红),SR为红
s->color = replace_node_parent->color;
replace_node_parent->color = rbtree_black;
if (s->right != nullptr)
s->right->color = rbtree_black;
rbtree_rotate_left(replace_node_parent, root);
break;
}
}
else
{
// del_node结点是其父结点的右子结点,镜像处理
rbtree_node_ptr s = replace_node_parent->left;
if (s->color == rbtree_red)
{
s->color = rbtree_black;
replace_node_parent->color = rbtree_red;
rbtree_rotate_right(replace_node_parent, root);
s = replace_node_parent->left;
}
if ((s->left == nullptr || s->left->color == rbtree_black)
&& (s->right == nullptr || s->right->color == rbtree_black))
{
s->color = rbtree_red;
replace_node = replace_node_parent;
replace_node_parent = replace_node_parent->parent;
}
else
{
if (s->left == nullptr || s->left->color == rbtree_black)
{
if (s->right != nullptr)
s->right->color = rbtree_black;
s->color = rbtree_red;
rbtree_rotate_left(s, root);
s = replace_node_parent->left;
}
s->color = replace_node_parent->color;
replace_node_parent->color = rbtree_black;
if (s->left != nullptr)
s->left->color = rbtree_black;
rbtree_rotate_right(replace_node_parent, root);
break;
}
}
}
if (replace_node != nullptr) replace_node->color = rbtree_black;
}
return del_node;
}
}
#endif
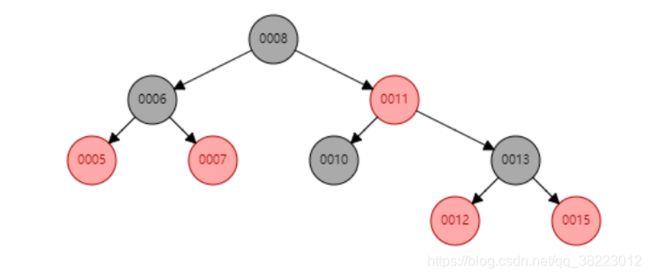
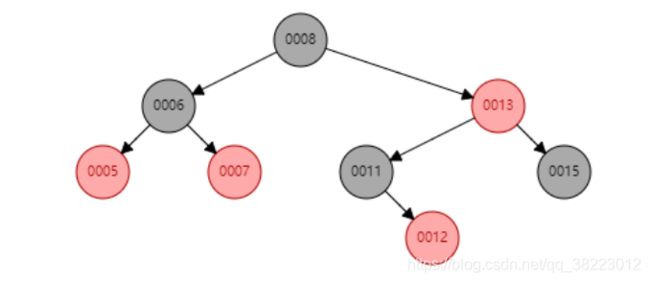
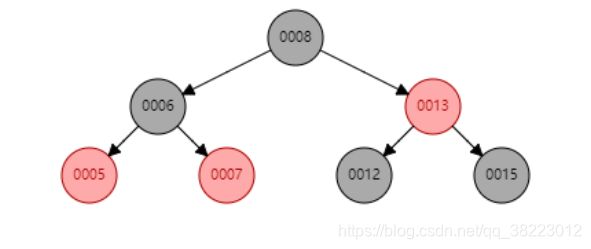
插入测试程序
顺序插入:10,7,8,15,5,6,11,13,12
stl_rb_tree_test.h
#pragma once
#include "../p2_STL_Source/stl_rb_tree.h"
namespace mySTL
{
namespace rbtreeTest
{
template<class Key, class Value>
using myRBTree = mySTL::rb_tree<Key, Value, mySTL::identity<int>, mySTL::less<int>>;
void test01();
}
}
stl_rb_tree_test.cpp
#include "stl_rb_tree_test.h"
#include