解决二叉树遍历相关问题(过程中深入一下C++递归程序栈编译和执行)
解决二叉树遍历相关问题(过程中深入一下C++递归程序栈编译和执行)
首先,事情是这样的:问题是求二叉树的根节点到某个节点的路径。
方法自然很多:树的后序遍历,图的BFS、DFS遍历等等。
这里,为了快速搞定代码先,就首先考虑了改造递归方式的后序遍历。
简单思路如下:
① 后续遍历,左右根
② 如果遍历到了目标节点:那么此时程序递归栈中,正常的话,从栈底到顶,应该刚好是待求路径
③ 在②的情况下,接下来得防止递归进入某个右子树,以至存好的路径被破坏。(左边不用考虑,因为后序遍历,待求节点的“左边”节点的递归,必然早已出了程序栈)
代码如下:
typedef struct BiTNode{
char data;
struct BiTNode * lchild, *rchild;
} BTNode, *BiTree;
//树的,先序,后序,中序,
///后序:(比如:求根到某个节点的路径)
bool flag = true;
char way[10000];
int i=0;
void PostOrder(BTNode* root, BiTree T, BTNode* destination){
BiTree p = T;
if(p == destination) flag = false; //如果 p指向了目标节点地址
if(p!=NULL){
PostOrder(root,p->lchild,destination);
if(flag){
PostOrder(root,p->rchild,destination);
}
}
if(!flag){//从找到目标节点之后,开始启动这个分支代码:
if(p!=NULL){
way[i++]=p->data;//反向记录路径
}
if(p == root) {//此时代表:找到目标元素后,程序栈已经回溯到树根,此时,倒序输出 way数组之后,即可退出程序
i--;
for(i;i>=0;i--){
cout<<way[i]<<" ";
}
return;
}
}
}
首先,必须承认,递归+条件判断,执行时间就是一个超级慢速的过程,不过这不是今天讨论的key。
按说,我这个思路应该是没毛病的,主函数调用测试代码如下:
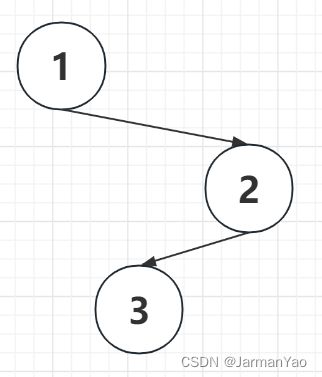
输出应为:1 2 3(查找到node3的路径)
int main(){
BTNode node = {'1',NULL,NULL};
BiTree T = &node;
BTNode node2 = {'2',NULL,NULL};;
T->rchild = &node2;
BTNode node3 = {'3',NULL,NULL};;
BiTree T3 = T->rchild;
T3->lchild = &node3;
PostOrder(T,T,T3->lchild);
}
① 值传递
VS地址传递
首先,如果我的函数是这样定义的话:(值传递,函数里的判断使用&目标值)
void PostOrder(BiTree root,BiTree T, BTNode destination){
if(p == &destination) flag = false; //如果 p指向了目标节点地址
。。。//其他内容省略
}
结果必然是错的,因为值传递,只是简单的将其值copy一份,传递给了子递归,这时候地址已经不是原来destination的地址了(我测试的,地址是随着函数嵌套在累减),(Java的spring中的BeanCopy功能,可以类比此过程)
测试代码:
void PostOrder(BiTree root,BiTree T, BTNode destination){
BiTree p = T;
if(p == &destination) flag = false; //如果 p指向了目标节点地址
cout<<"p="<<p<<"\t\t"<<"&destination="<<&destination<<endl;
if(p!=NULL){
PostOrder(root,p->lchild,destination);
if(flag){
PostOrder(root,p->rchild,destination);
}
}
if(!flag){//从找到目标节点之后,开始启动这个分支代码:
if(p!=NULL){
way[i++]=p->data;//反向记录路径
}
if(p == root) {//此时代表:找到目标元素后,程序栈已经回溯到树根,此时,倒序输出 way数组之后,即可退出程序
i--;
for(i;i>=0;i--){
cout<<way[i]<<" ";
}
return;
}
}
}
int main(){
BTNode node = {'1',NULL,NULL};
BiTree T = &node;
BTNode node2 = {'2',NULL,NULL};;
T->rchild = &node2;
BTNode node3 = {'3',NULL,NULL};;
BiTree T3 = T->rchild;
T3->lchild = &node3;
PostOrder(T,T,node3);
// PostOrder(T,T,T3->lchild);
}
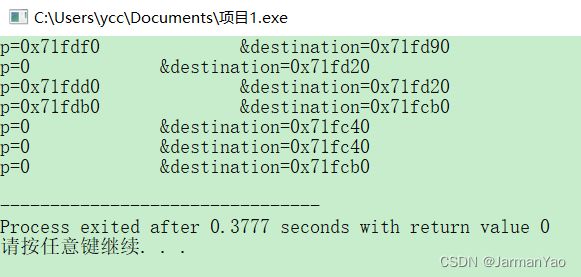
这里分析一下地址累减的原因:必然是因为计算机底层的程序栈,栈底在高地址部分,然后嵌套的子函数依次在下面低地址部分。&destination相等的部分,是因为在程序递归树的同一层。
这里从计算机组成原理的角度考虑,大致就是如下图所示的底层存储逻辑:
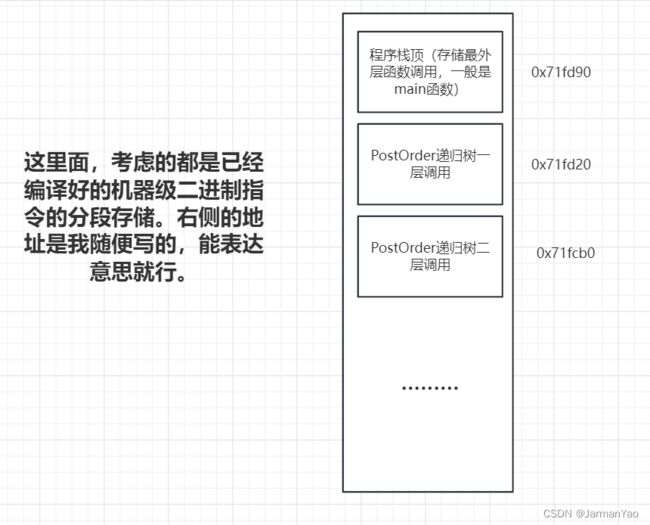
其实从汇编语言层面理解,也可以:
调用上一层函数的变量的时候,指令一般是指定寄存器进行加字或字节的某整数倍
调用本层函数的变量的时候,指令一般是指定寄存器进行减字或字节的某整数倍
② 考虑问题的时候,不能将关键判断使用第一层调用传递的destination地址,也就是说,必须得保证某个传递地址一直保持不变的状态
直接来例子吧,代码如果这样写:
void PostOrder(BiTree T, BTNode *destination){
BiTree p = T;
if(p == destination) flag = false; //如果 p指向了目标节点地址
if(p!=NULL){
PostOrder(p->lchild,destination);
if(flag){
PostOrder(p->rchild,destination);
}
}
if(!flag){//从找到目标节点之后,开始启动这个分支代码:
if(p!=NULL){
way[i++]=p->data;//反向记录路径
}
if(p == T) {//此时代表:找到目标元素后,程序栈已经回溯到树根,此时,倒序输出 way数组之后,即可退出程序
i--;
for(i;i>=0;i--){
cout<<way[i]<<" ";
}
return;
}
}
}
之所以刚开始这样定义函数,我考虑的是等待代码中的左右两个分支问题搞定后,代码自己就回到首次调用了,而这时候的T地址就是最开始那个根,于是乎,我就暂时忽略了递归回溯过程中,T地址一步一步加回栈顶的过程中对分支结构下面那部分if代码的调用。
相信眼尖的一下就看到问题所在了,p==T恒成立,所以不会输出任何东西(因为i都嘎子负数了,还输出个锤子,想想晚上写代码就是脑子瓦特)。
OK,over,有很多CO底层知识,我这里没有深入去解释,但是确实CO知识的存储,对写代码时的理解程度会深一些,确有体会,比如写函数的时候,会想到分段式存储、编译后指令排列的可能顺序,递归过程和回溯过程中地址的传递和变化等等。
