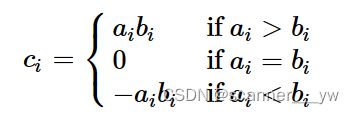Codeforces Round 665 (Div. 2) (A-F)
A.Problem - A - Codeforces
(1)题意
给你个X轴,初始A点在n这个位置,O在源点0,问你要把B放在哪才能让|AB-BO| = k,最小化A需要移动多少次。
(2)思路
直接分情况套路即可。
(3)代码
#include
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair
#define fi first
#define se second
#define vi vector
#define vl vector
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 2e5 + 10;
void solve()
{
int n,k;
cin >> n >> k;
int Ans = 0;
if((n + k) & 1) {
Ans ++;
n ++;
}
if(k > n) Ans += k - n;
cout << Ans << '\n';
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T = 1;
cin >> T;
while(T --) solve();
return 0;
} B.Problem - B - Codeforces
(1)题意
a序列有x1个0,y1个1,z1个2,b序列有x2个0,y2个1,z2个2,给定你这个函数,问你在任意排序后可以获得的最大价值是多少。
(2)思路
贪心考虑,肯定是先把有价值的拿了,然后把其他的都给弄成0,否则就只能加上负贡献了。
(3)代码
#include
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair
#define fi first
#define se second
#define vi vector
#define vl vector
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 2e5 + 10;
void solve()
{
int x1,y1,z1;
int x2,y2,z2;
int Ans = 0;
cin >> x1 >> y1 >> z1;
cin >> x2 >> y2 >> z2;
int mi = min(z1,y2);
y2 -= mi,z1 -= mi;
Ans += mi * 2;
mi = min(z1,z2);
z1 -= mi,z2 -= mi;
mi = min(z1,x2);
z1 -= mi,x2 -= mi;
mi = min(y1,y2);
y1 -= mi,y2 -= mi;
mi = min(y1,x2);
y1 -= mi,x2 -= mi;
mi = min(x1,z2);
x1 -= mi,z2 -= mi;
mi = min(x1,y2);
x1 -= mi,y2 -= mi;
mi = min(y1,y2);
y1 -= mi,y2 -= mi;
mi = min(x1,x2);
x1 -= mi,x2 -= mi;
mi = min(z1,z2);
z1 -= mi,z2 -= mi;
mi = min(y1,z2);
Ans -= 2 * mi;
cout << Ans << '\n';
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T = 1;
cin >> T;
while(T --) solve();
return 0;
} C.Problem - C - Codeforces
(1)题意
给你一个长为n的序列,设最小值为Mi,你每次可以选择两个数a[i]和a[j],若gcd(a[i],a[j])=Mi,问你是否可以把这个序列变成不降序列。
(2)思路
很显然我们可以直接把%Mi为0的所有数拿出来,从大到小依次放入原序列,最后检查原序列是否不降即可。
(3)代码
#include
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair
#define fi first
#define se second
#define vi vector
#define vl vector
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 2e5 + 10;
int a[N];
void solve()
{
int n;
cin >> n;
int mi = 1e9;
vector v;
rep(i,1,n) {
cin >> a[i];
mi = min(mi,a[i]);
}
rep(i,1,n) {
if(a[i] % mi == 0) {
v.pb(a[i]);
}
}
sort(v.rbegin(),v.rend());
rep(i,1,n) {
if(a[i] % mi == 0) {
a[i] = v.back();
v.pop_back();
}
}
rep(i,2,n) {
if(a[i] < a[i - 1]) {
cout << "NO" << '\n';
return;
}
}
cout << "YES" << '\n';
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T = 1;
cin >> T;
while(T --) solve();
return 0;
} D.Problem - D - Codeforces
(1)题意
给你棵N个节点的树,和一个总权值K,要你把K分配给这颗树的N-1条边,满足这些树边相乘等于K,并且分配的边权1的数量最少,问你任意两个点的所有边权和加起来最大为多少?
(2)思路
我们可以计算出每条边经过多少次,因此考虑贪心分配边权即可,若K分解的质因子大于当前n - 1,则需要把后面的补成1即可,否则可以把多余的补给经过次数最多的那条边即可。
(3)代码
#include
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair
#define fi first
#define se second
#define vi vector
#define vl vector
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 1e5 + 10;
vector g[N];
ll f[N],siz[N];
int n;
const ll mod = 1e9 + 7;
inline void dfs(int u,int f)
{
siz[u] = 1;
for(auto v : g[u]) {
if(v == f) continue;
dfs(v,u);
siz[u] += siz[v];
}
}
void solve()
{
cin >> n;
rep(i,1,n) g[i].clear();
rep(i,2,n) {
int u,v;
cin >> u >> v;
g[u].pb(v),g[v].pb(u);
}
int k;
cin >> k;
vector z;
rep(i,1,k) cin >> f[i];
dfs(1,0);
rep(i,2,n) z.pb(siz[i] * (n - siz[i]));
ll Ans = 0;
if(sz(z) >= k) {
sort(f + 1,f + 1 + k,[&](ll &c,ll &d){
return c > d;
});
sort(z.rbegin(),z.rend());
while(sz(z) > k) f[++ k] = 1;
rep(i,1,sz(z)) Ans = (Ans + f[i] * z[i - 1] % mod) % mod;
}
else {
sort(f + 1,f + 1 + k,[&](ll &c,ll &d){
return c < d;
});
sort(z.begin(),z.end());
ll tmp = 1,res = k - sz(z);
for(int i = k - res + 1;i <= k;i ++) tmp = tmp * f[i] % mod;
f[sz(z)] = f[sz(z)] * tmp % mod;
rep(i,1,sz(z)) Ans = (Ans + f[i] * z[i - 1] % mod) % mod;
}
cout << Ans << '\n';
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T = 1;
cin >> T;
while(T --) solve();
return 0;
} E.Problem - E - Codeforces
(1)题意
给你N条平行X轴的线,和M条平行Y轴的线,保证每一条线都与边框至少有一个交点,且每一条线不重合,问你最后会分出来多少个矩形。
(2)思路
这种题目一般是看交点就行了,因此我们观察样例很容易得出结论,答案=交点个数+1+本身交边框有两交点的线。
那么我们可以用值域树状数组维护出来即可,用树状数组代表横坐标为多少时有一条长度为y的线,然后对于每一条平行Y轴的线做区间查找即可得出交点个数。
(3)代码实现
#include
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair
#define fi first
#define se second
#define vi vector
#define vl vector
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 1e6 + 10;
template
struct Fenwick {
const int n;
std::vector a;
Fenwick (int n) : n(n), a(n + 1) {}
void add(int pos, T x) {
for (int i = pos; i <= n; i += i & -i) {
a[i] += x;
}
}
T query(int x) {
T res = 0;
for (int i = x; i; i -= i & -i) {
res += a[i];
}
return res;
}
T query(int l, int r) {
if (l == 0 || l > r) {
return 0;
}
return query(r) - query(l - 1);
}
//找到大于k得第一个地方
T kth(int k) {
int pos = 0;
for(int j = 31 - __builtin_clz(n);j >= 0;j --) {
if(pos + (1 << j) <= n && k > a[pos + (1 << j)]) {
pos += 1 << j;
k -= a[pos];
}
}
return pos + 1;
}
};
//使用Fenwick fen(n)
vector a[N],b[N];
void solve()
{
int n,m;
cin >> n >> m;
Fenwick fen(1000001);
ll Ans = 1;
rep(i,1,n) {
int y1,x1,x2;
cin >> y1 >> x1 >> x2;
a[x1].pb({y1 + 1,1});
a[x2 + 1].pb({y1 + 1,-1});
if(x1 == 0 && x2 == 1000000) Ans ++;
}
rep(i,1,m) {
int x1,y1,y2;
cin >> x1 >> y1 >> y2;
b[x1].pb({y1 + 1,y2 + 1});
if(y1 == 0 && y2 == 1000000) Ans ++;
}
rep(i,0,1000000) {
for(auto [x,w]: a[i]) {
fen.add(x,w);
}
for(auto [l,r] : b[i]) {
Ans += fen.query(l,r);
}
}
cout << Ans;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T = 1;
// cin >> T;
while(T --) solve();
return 0;
} F.Problem - F - Codeforces
第一个操作和第四个操作是线段树基本操作,因此不需要管,重点观察第二个操作和第三个操作,首先这颗线段树是一颗完美二叉树,包含的区间都是2^i次方,对于reverse操作来说,就是把第(k + 1)层线段树的节点的左右儿子交换,那么swap操作,其实也就是对于每一层线段树节点的左右儿子进行交换,那么这个问题就是个简单的线段树了,交换直接在外边维护好就行了。
(3)代码
#include
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair
#define fi first
#define se second
#define vi vector
#define vl vector
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 3e5 + 10;
ll tr[N << 2];
int a[N],rev[N];
inline void build(int u,int l,int r)
{
if(l == r) {
tr[u] = a[l];
return;
}
int mid = (l + r) >> 1;
build(u << 1,l,mid);
build(u << 1 | 1,mid + 1,r);
tr[u] = tr[u << 1] + tr[u << 1 | 1];
}
inline void modify(int u,int l,int r,int dep,int p,int x)
{
if(l == r) {
tr[u] = x;
return;
}
int mid = (l + r) >> 1;
if(p <= mid) modify(u << 1 ^ rev[dep],l,mid,dep - 1,p,x);
else modify(u << 1 | 1 ^ rev[dep],mid + 1,r,dep - 1,p,x);
tr[u] = tr[u << 1] + tr[u << 1 | 1];
}
inline ll query(int u,int l,int r,int dep,int ql,int qr)
{
if(l >= ql && r <= qr) return tr[u];
int mid = (l + r) >> 1;
ll s = 0;
if(ql <= mid) s += query(u << 1 ^ rev[dep],l,mid,dep - 1,ql,qr);
if(qr > mid) s += query(u << 1 | 1 ^ rev[dep],mid + 1,r,dep - 1,ql,qr);
return s;
}
void solve()
{
int n,q;
cin >> n >> q;
rep(i,1,(1 << n)) cin >> a[i];
build(1,1,(1 << n));
while(q --) {
int op,l,r;
cin >> op;
if(op == 1) {
cin >> l >> r;
modify(1,1,(1<> l;
for(int i = 0;i <= l;i ++) rev[i] ^= 1;
}
else if(op == 3) {
cin >> l;
rev[l + 1] ^= 1;
}
else {
cin >> l >> r;
cout << query(1,1,(1<> T;
while(T --) solve();
return 0;
}