不过是一棵红黑树（附源码）

前言

红黑树,可谓是名号响当当的一种数据结构了。在数据结构学习的初期我们了解到了搜索二叉树，并且知道搜索二叉树的效率是非常之高的，在理想情况下10亿个数据中找一个值它也只需要30次左右，但是它尽管如此厉害可是也有不足的地方，在一些极端情况下，搜索二叉树可能会被退化成一棵单链表，那么此时它的效率就会大打折扣的变成O(n)。

红黑树的性质

在了解搜索二叉树的牛逼和不足之处之后，我们的某个大佬就想，能不能让一棵树无论在什么情况下都保持接近理想状态呢。这是红黑树就由此诞生了。先来看看红黑树的几个性子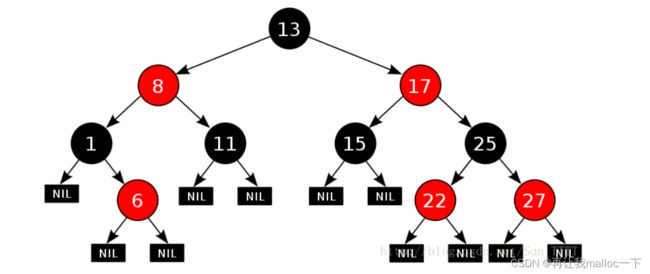

1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的，则它的两个孩子结点是黑色的
4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均 包含相同数目的黑色结点
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点）

只要满足了这5个条件，那么就能够做到最长路劲不超过最短路劲的二倍，为什么这样说我们通过这样一张图了解一下。

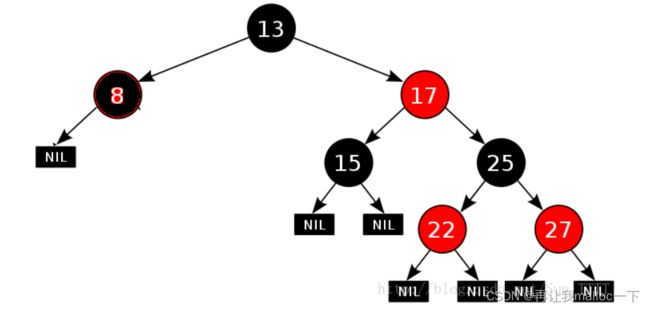在最极端的情况下，左边连续黑色节点，而右边最多是一红一黑，如果继续往右边添加黑色节点就会违背第4条规则。

红黑树的实现

在了解到红黑树的性质之后，接下来我们就去实现这样效率之高的一棵树。

首先，当我们对一堆数据需要用红黑树的结构来进行管理的时候，那么在对数据进行插入的时候就要按照红黑色树的规则进行处理。假想现在有这样一个场景

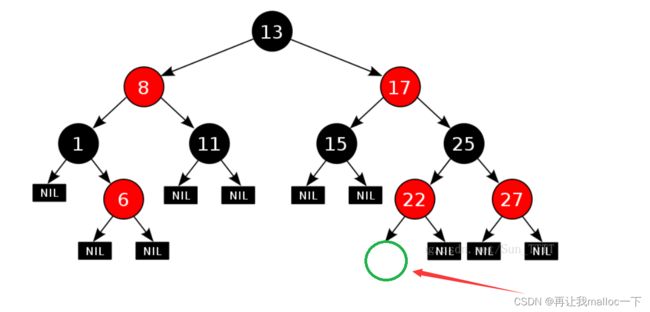假设我们需要在这个位置插入一个值，那么插入的这个值我们应该把它处理成什么颜色呢，如果是红色的话就会违背规则3，如果是黑色的话就会违背规则4。这就好比，今天你必须要犯一个错误，第一个错误呢就是你去把你弟弟的王者卸载掉，而第二个错误就是中午吃饭的时候你把桌子掀掉。这样对比一下呢就是第一个错误你只会让你弟弟不高兴，而第二个错误呢会让一家人都不高兴，孰轻孰重一眼能看出来。所以我在进行插入的时候就选择插入一个红色的节点。

但是回过头一想，如果你让你弟弟不高兴了自己也一天会膈应。所以呢这个时候你的爷爷，爸爸，叔叔这样的长辈就会来劝你两，说哥哥卸载你的游戏是因为你一天作业不做就只顾着玩。然后呢你弟弟在长辈的劝说下又和你重归于好了。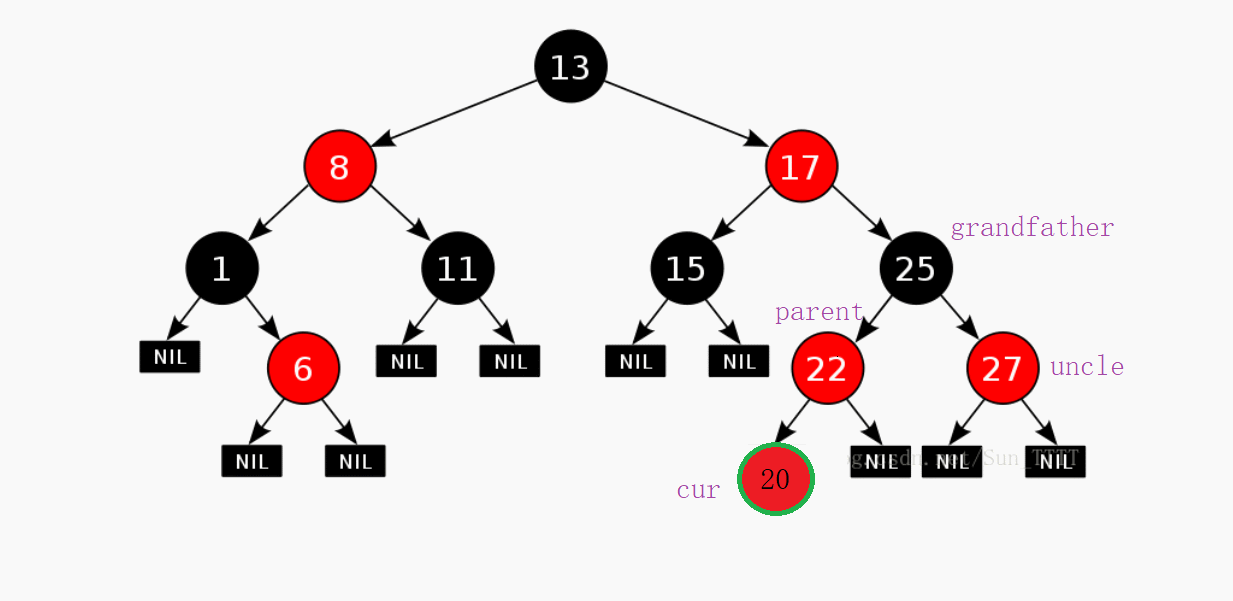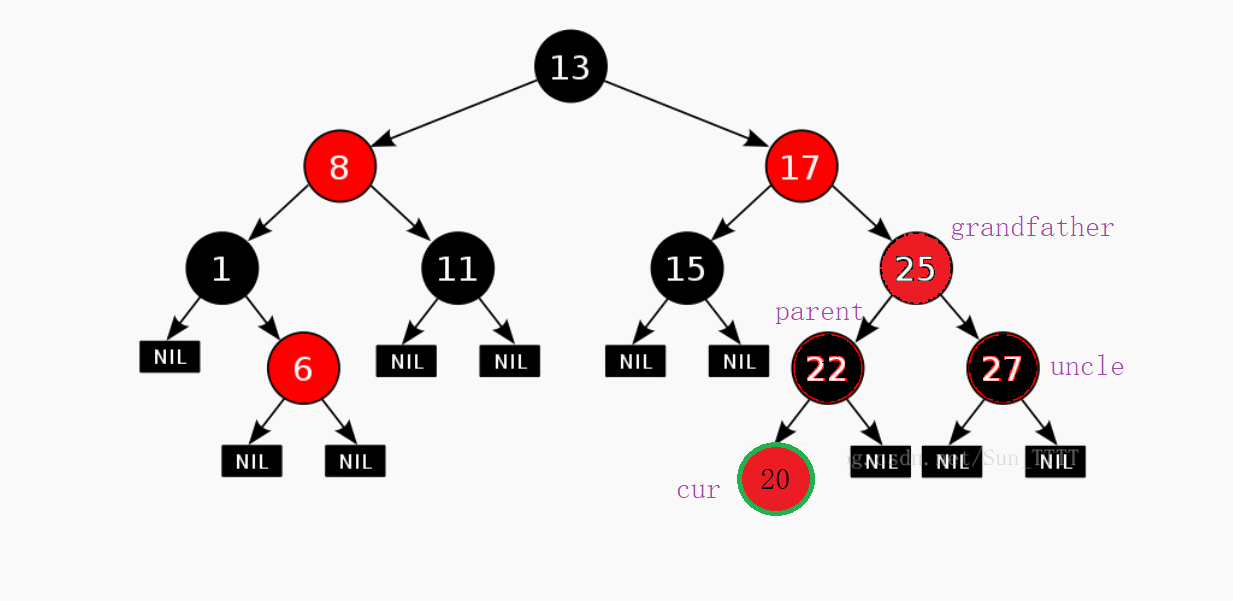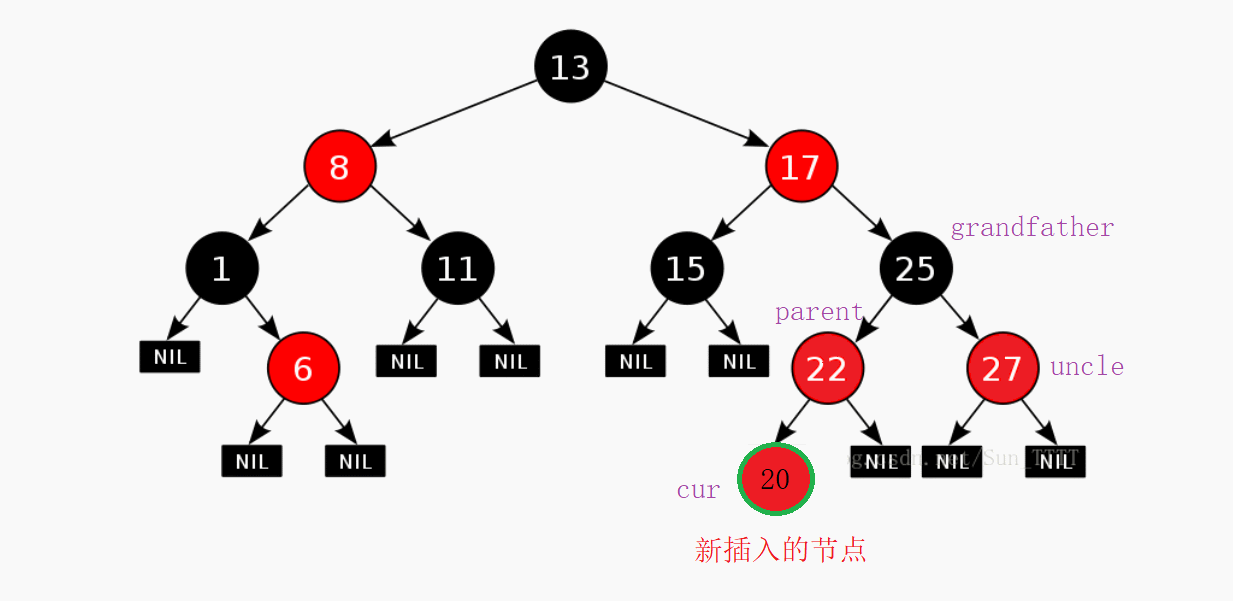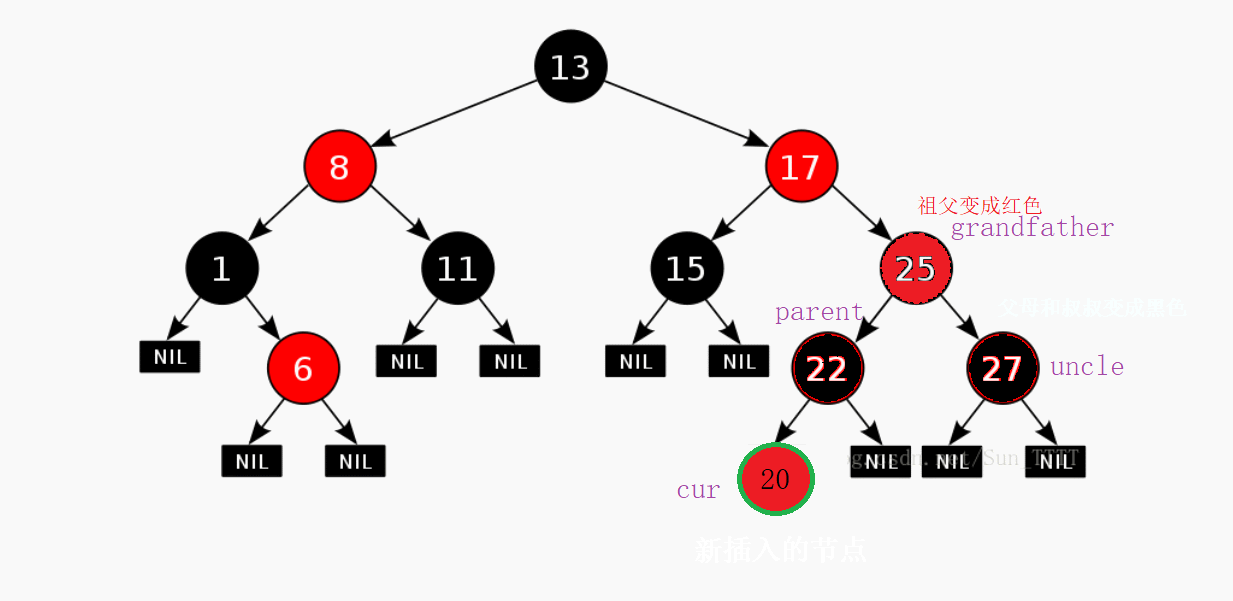

这样呢就既不违背规则又把节点给插入进去了。如果祖父被改成红色之后并且祖父的父亲也是红色，那么我们需要按照这个逻辑继续往上走，让cur成为祖父，parent成为新祖父的父母，grandfather成为parent的父母。

那么问题又来了，如果在爸爸是独生子的情况下，如果按照上面的逻辑将爸爸改成黑色，祖父改成红色

最后就会违背第4条规则，所以当叔叔不存在的时候，我们对其颜色改造之后，在进行旋转一下，让cur做parent的左边，grandfather做parent的右边，这样既不违背搜索二叉树的规则，又不违背红黑树的规则

树的插入可能有无数种情况，但是我们就只需要考虑到这三种情况，因为这三种情况就可以掩盖所有插入的可能，我们通过这张图可以了解到

#define _CRT_SECURE_NO_WARNINGS 1
#include
#include
using namespace std;

//节点中的颜色
enum Color
{
	RED,
	BLOCK
};

//红黑树的节点
template
struct RBTreeNode
{
	RBTreeNode* _left;
	RBTreeNode* _right;
	RBTreeNode* _parent;
	pair _kv;
	Color _color;
	
	RBTreeNode(const pair kv,Color col=BLOCK)
		:_kv(kv)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		,_color(col)
	{}
};



template
class RBTree
{
	typedef RBTreeNode Node;
public:
	RBTree()
		:_root(nullptr)
	{}
	bool insert(const pair kv)
	{
		//树为空
		if (_root == nullptr)		//如果当前树为空直接插入节点并将颜色改成黑色即可
		{
			_root = new Node(kv);
			_root->_color = BLOCK;
			return true;
		}
		
		//树不为空
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			if (cur->_kv.first > kv.first)	//按照搜索二叉树的特征往合适的位置往下找
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;	//如果需要插入的节点值已经有了就退出
			}
		}

		//找到为空可以插入的位置需要判断是否比当前值大或者小
		cur = new Node(kv);
		cur->_color = RED;
		if (parent->_kv.first > kv.first)
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}
		cur->_parent = parent;

		//uncle存在并且uncle为红色  如果父亲存在并且父亲的颜色为红色
		while (parent && parent->_color == RED)
		{
			//祖父
			Node* grandfather = parent->_parent;
			if (parent == grandfather->_left)	//如果parent在grandfather的左边
			{
				Node* uncle = grandfather->_right;

				//uncle存在并且为红色
				if (uncle && uncle->_color == RED)
				{
					parent->_color = uncle->_color = BLOCK;
					grandfather->_color = RED;

					//继续向上处理
					cur = grandfather;
					parent = cur->_parent;
				}

				//uncle不存在
				else
				{
					if (cur == parent->_left)	//如果cur存在的是parent的左边只需要单纯的进行右旋
					{
						//		g
						//    p
						//  c
						RotateR(grandfather);

						grandfather->_color = RED;
						parent->_color = BLOCK;
					}
					else if(cur == parent->_right)//如果cur存在右边就需要进行左右双旋
					{
						//		g
						//   p
						//     c
						RotateL(parent);
						RotateR(grandfather);

						cur->_color = BLOCK;
						grandfather->_color=parent->_color = RED;
					}
				}	
			}

			//如果parent存在grandfather的右边
			else if (parent == grandfather->_right)
			{
				Node* uncle = grandfather->_left;	
				if (uncle && uncle->_color == RED)
				{
					parent->_color = uncle->_color = BLOCK;
					grandfather->_color = RED;

					//继续向上处理
					cur = grandfather;
					parent = cur->_parent;
				}

				//uncle不存在
				else
				{
					if (cur == parent->_right)
					{
						//		g
						//			p
						//				c
						RotateL(grandfather);

						grandfather->_color = cur->_color = RED;
						parent->_color = BLOCK;
					}
					else
					{
						//		g
						//			p
						//		 c
						RotateR(parent);
						RotateL(grandfather);

						cur->_color = BLOCK;
						grandfather->_color = parent->_color = RED;
					}
				}
			}
		}
		_root->_color = BLOCK;	
		return true;
	}


	//左旋
	void RotateL(Node* parent)
	{
		//		p
		//			c
		//				t	
		Node* cur = parent->_right;
		Node* curleft = cur->_left;
		parent->_right = curleft;

		//如果cur的左子树不为空将curleft的父亲指向parent
		if (curleft)
			curleft->_parent = parent;

		//让cur的左边指向parent
		cur->_left = parent;
		

		//有可能当前树是另一颗树的子树,只有当前树正在被修复
		Node* ppnode = parent->_parent;

		parent->_parent = cur;
		//如果parent不是另一棵树的子树就直接让cur变成root
		if (parent == _root)
		{
			_root = cur;
			cur->_parent = nullptr;
		}

		//判断parent是ppnode的左子树还是右子树
		else if (ppnode->_left == parent)
		{
			ppnode->_left = cur;
		}
		else if (ppnode->_right == parent)
		{
			ppnode->_right = cur;
		}
		cur->_parent = ppnode;
	}

	//右旋
	void RotateR(Node* parent)
	{
		//		g
		//    p
		//  c
		Node* cur = parent->_left;
		Node* curright = cur->_right;

		parent->_left = curright;

		if (curright)
			curright->_parent = parent;

		cur->_right = parent;

		Node* ppnode = parent->_parent;
		parent->_parent = cur;

		if (parent == _root)
		{
			_root = cur;
			cur->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
				ppnode->_left = cur;
			else
				ppnode->_right = cur;

			cur->_parent = ppnode;
		}
	}

	bool IsBalance()
	{
		return IsBalance(_root);
	}

	bool checkcolor(Node* root,int blocknum,int sum)
	{
		if (root == nullptr)
		{
			if (blocknum != sum)		//如果任意一条线路上的黑色节点和基准值不同就说明路径上的黑色节点不同
			{
				cout << "黑色节点不准确" << endl;
				return false;
			}
			else
			{
				return true;
			}
		}
			
		if (root->_color == BLOCK)	//记录黑色节点
			blocknum++;

		if (root->_color == RED && root->_parent && root->_parent->_color == RED)	//如果当前节点和父亲节点都为红色说明树有问题
		{
			cout << "出现了连续红色节点：" << root->_kv.first  << endl;
			return false;
		}
		
		return checkcolor(root->_left,blocknum,sum)
			&& checkcolor(root->_right, blocknum, sum);
	}
	bool IsBalance(Node* root)
	{
		if (root == nullptr)	
			return true;
		if (root->_color != BLOCK)	//检查第一个节点如果不为黑色就说明出问题了
			return false;

		//统计一条路径上的黑色数量
		int sum = 0;
		Node* num = _root;
		while (num)
		{
			if (num->_color == BLOCK)
				sum++;
			num = num->_left;
		}

		return checkcolor(root,0,sum);
	}

private:
	Node* _root;
};



//测试
#define _CRT_SECURE_NO_WARNINGS 1
#include"RBTree.h"


int main()
{
	//srand((size_t)time(0));
	int arr[] = { 2,8,6,10,14,38,7,9,80,65,72,64,10};
	RBTree t;								
	for (auto e : arr)
	{
		t.insert(make_pair(e, e));
	}
	t.IsBalance();
	return 0;
}