自定义类型(结构体、枚举、联合)
今天追秋给大家带来的自定义类型,其中包含的干货是非常多的,也希望大家在观看的时候留下一些宝贵的建议。
结构体
结构的基础知识
结构是一些值的集合,这些值称为成员变量。结构的每个成员可以是不同类型的变量。
结构的声明
struct Stu
{
char name[20];//名字
int age;//年龄
char sex[5];//性别
char id[20];//学号
}; //分号不能丢
特殊的声明
在声明结构的时候,可以不完全的声明。
例如:
struct
{
int a;
char b;
float c;
}x;
此处将结构体名省略,只能依靠结构体变量x来进行操作,且只能使用一次!
结构体自引用
举例:
//代码1
struct Node
{
int data;
struct Node next;
};
//可行否?
如果可以,那sizeof(struct Node)是多少?
**这种结构体的包含方式是错误的,无法计算结构体的大小;在编译的是编译器会报错!**因此对这段代码进行修改:
//代码2
struct Node
{
int data;
struct Node* next;
修改后,结构体内包含的是一个结构体指针,是指针,大小就是4/8个字节,此时该结构体的大小可以计算。
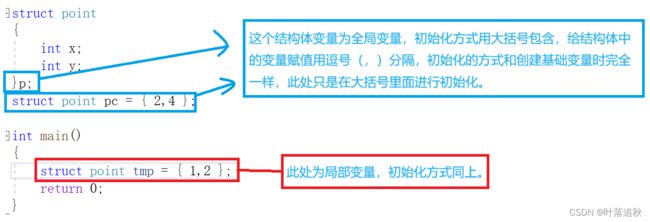
结构体变量的定义和初始化
struct point
{
int x;
int y;
}p;
struct point pc = { 2,4 };
int main()
{
struct point tmp = { 1,2 };
return 0;
}
结构体的内存对齐
结构体的内存对齐是用来计算结构体大小的必要知识,是学习结构体的重点也是难点,下面我来为大家好好讲解以下这个知识点。
还是老样子,先举例:
{
char c1;
int i;
char c2;
};
printf("%d\n", sizeof(struct S1));
//练习2
struct S2
{
char c1;
char c2;
int i;
};
printf("%d\n", sizeof(struct S2));
运行结果:
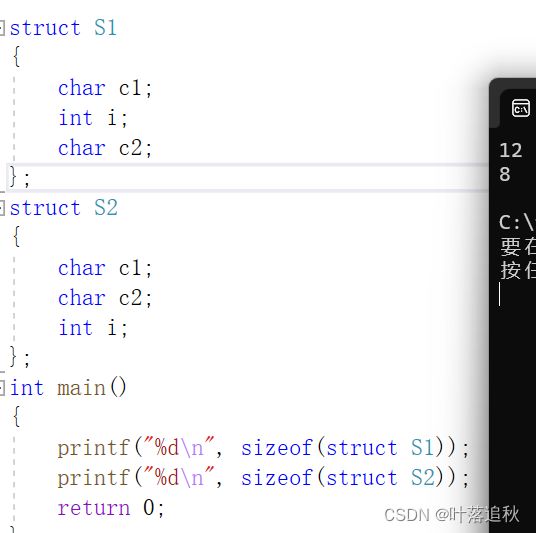
我们可以看懂,在定义的结构体S1和S2中,数据的类型和数量都是相同的,那为什么大小却不一样呢?同样的其中的数据类型按照常规计算来看,明明只需要六个字节就可以将数据完成存储,但是这两个结构体的大小是12和8。下面给大家仔细讲解一下:
如何计算?
首先得掌握结构体的对齐规则:
- 第一个成员在与结构体变量偏移量为0的地址处。
- 其他成员变量要对齐到某个数字(对齐数)的整数倍的地址处。对齐数 = 编译器默认的一个对齐数 与 该成员大小的较小值。VS中默认的值为8
- 结构体总大小为最大对齐数(每个成员变量都有一个对齐数)的整数倍。
- 如果嵌套了结构体的情况,嵌套的结构体对齐到自己的最大对齐数的整数倍处,结构体的整体大小就是所有最大对齐数(含嵌套结构体的对齐数)的整数倍。
拿第一个例子来看:
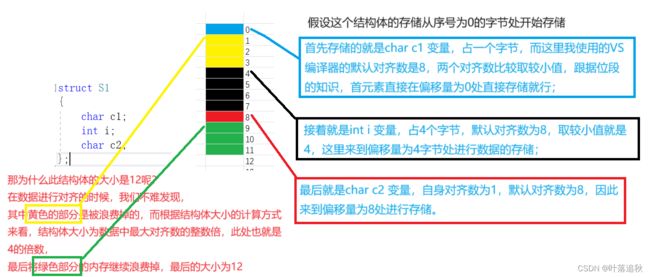
同理我们可以就可以通过计算来得到第二个结构体的大小;
那么为什么会出存在内存对齐呢?
- 平台原因(移植原因):
不是所有的硬件平台都能访问任意地址上的任意数据的;某些硬件平台只能在某些地址处取某些特定类型的数据,否则抛出硬件异常。- 性能原因:
数据结构(尤其是栈)应该尽可能地在自然边界上对齐。
原因在于,为了访问未对齐的内存,处理器需要作两次内存访问;而对齐的内存访问仅需要一次访问。
总体来说:
结构体的内存对齐是拿空间来换取时间的做法。
所以我们在进行结构体设计的时候,尽量要将占用空间小的数据放在一起。
修改默认对齐数
#include 顾名思义:此处#pragma pack(8)是一个宏,可以将默认对齐数设置为8,但是仅限于结构体S1范围内,后面的#pragma pack()命令会将自定义对齐数取消,恢复到系统默认对齐数。
结构体传参
struct S
{
int data[1000];
int num;
};
struct S s = {{1,2,3,4}, 1000};
//结构体传参
void print1(struct S s)
{
printf("%d\n", s.num);
}
//结构体地址传参
void print2(struct S* ps)
{
printf("%d\n", ps->num);
}
int main()
{
print1(s); //传结构体
print2(&s); //传地址
return 0;
}
以上两种结构体传参的方式中,毋庸置疑,当然是结构体传址更加方便并且占用的内存中间更少,因此我们在进行结构体传参的时候尽量使用传址调用。
位段
什么是位段
位段的声明和结构是类似的,有两个不同:
1.位段的成员必须是 int、unsigned int 或signed int 。
2.位段的成员名后边有一个冒号和一个数字。
比如:
struct A
{
int _a:2;
int _b:5;
int _c:10;
int _d:30;
};
位段的内存分配
- 位段的成员可以是 int unsigned int signed int 或者是 char (属于整形家族)类型
- 位段的空间上是按照需要以4个字节( int )或者1个字节( char )的方式来开辟的。
- 位段涉及很多不确定因素,位段是不跨平台的,注重可移植的程序应该避免使用位段
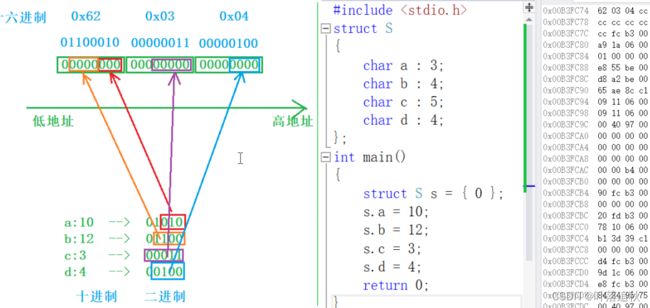
//一个例子
struct S
{
char a:3;
char b:4;
char c:5;
char d:4;
};
struct S s = {0};
s.a = 10;
s.b = 12;
s.c = 3;
s.d = 4;
//空间是如何开辟的?
注意:我们在使用位段的时候,可能会造成数据的丢失,因此在不确定数据大小范围的情况下不要使用位段。
位段的跨平台问题
- int 位段被当成有符号数还是无符号数是不确定的。
- 位段中最大位的数目不能确定。(16位机器最大16,32位机器最大32,写成27,在16位机器会出问题。
- 位段中的成员在内存中从左向右分配,还是从右向左分配标准尚未定义。
- 当一个结构包含两个位段,第二个位段成员比较大,无法容纳于第一个位段剩余的位时,是舍弃剩余的位还是利用,这是不确定的。
总结:
跟结构相比,位段可以达到同样的效果,但是可以很好的节省空间,但是有跨平台的问题存在
枚举
枚举顾名思义就是一一列举。
把可能的取值一一列举。
比如我们现实生活中:一周的天数为七天,彩虹的七种颜色,红绿灯的颜色,人的性别这些都是可以一一列举出来的;
下面还是老样子,直接上代码:
enum Sex//性别
{
MALE,
FEMALE,
SECRET
};
enum Color//颜色
{
GREEN,
RED,
BLACK
};
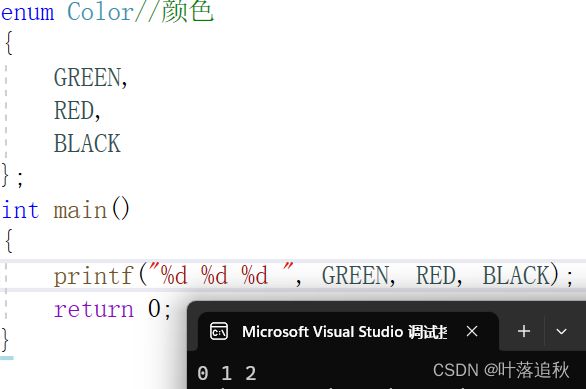
那我们是否可以对枚举类型的可能取值进行打印呢?
我们可以看到,枚举类型其中的可能取值是从0开始一次递增的,当然我们也是可以去改变枚举类型其中可能取值的大小:
如上图:当我们对枚举类型的可能取值进行赋值的时候,其中的值就会被更改;
从上图可以看到,当我们更改第一个可能取值的值得时候,其它得值会依次递增1。
那我们是否可以去计算一个枚举类型的大小呢?
下面直接上代码:
enum Color//颜色
{
GREEN=5,
RED,
BLACK
};
int main()
{
enum Color color = GREEN;
printf("%zd ", sizeof(color));
return 0;
}
枚举的优点
为什么使用枚举?
我们可以使用 #define 定义常量,为什么非要使用枚举?
枚举的优点:
- 增加代码的可读性和可维护性
- 和#define定义的标识符比较枚举有类型检查,更加严谨。
- 防止了命名污染(封装)
- 便于调试
- 使用方便,一次可以定义多个常量
解析:
这里解释一下枚举类型和#define定义的类型的区别;
用#define定义的常量在使用的时候是不会经过类型检查的,我们知道:枚举常量是有类型的,也就是枚举类型,在使用的时候只能给枚举变量赋值,而用#define定义的常量给其它常量赋值的时候是不会经过类型检查,直接进行替换的;
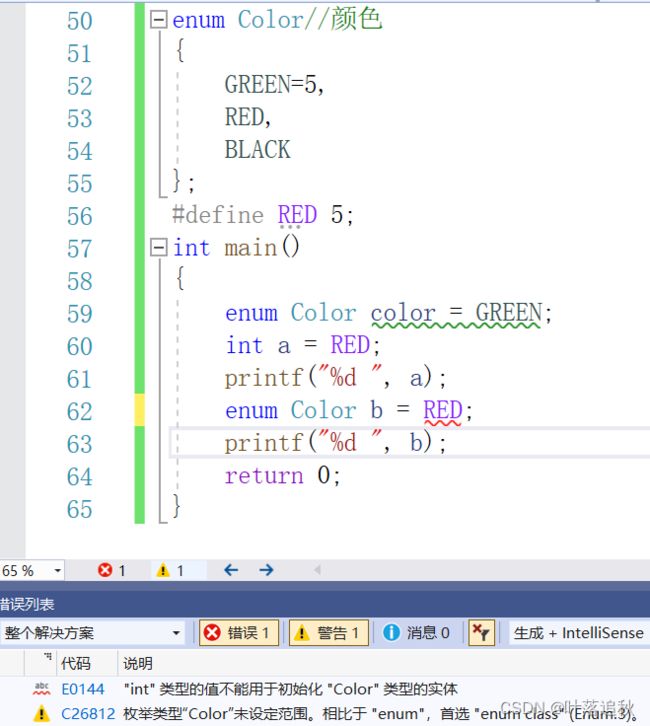
下面举例:
可以看到RED常量分别在赋值给整形和枚举类型的变量是结果不同,当赋值给枚举变量的时候编译器报错。
以上代码在C语言环境下是不会报错的,但是在C++环境下就会报错,因为C++的类型检查更加严谨
联合体
联合体的定义
联合也是一种特殊的自定义类型
这种类型定义的变量也包含一系列的成员,特征是这些成员公用同一块空间(所以联合也叫共用体)。
//联合类型的声明
union Un
{
char c;
int i;
};
//联合变量的定义
union Un un;
联合体的特点
联合的成员是共用同一块内存空间的,这样一个联合变量的大小,至少是最大成员的大小(因为联合至少得有能力保存最大的那个成员)
union Un
{
int i;
char c;
};
int main()
{
union Un un;
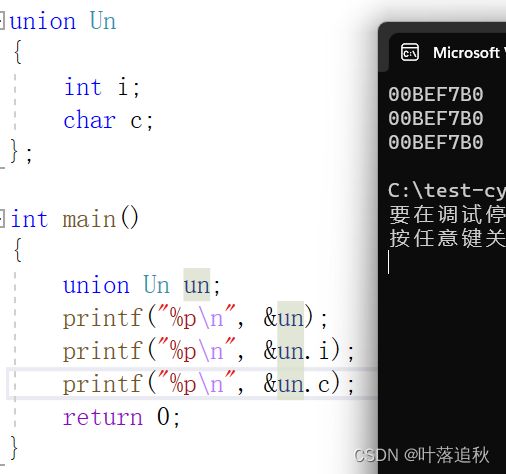
printf("%p\n", &un);
printf("%p\n", &un.i);
printf("%p\n", &un.c);
return 0;
}
//下面输出的结果是什么?
运行结果:
可以看到,当我们打印结果的时候,联合体中定义的常量的地址是相同的,可以看出它们公用一块空间,知道这个我们可以写一段代码:确定当前机器的大小端存储。
下面看代码:
union Un
{
int i;
char c;
};
int main()
{
union Un un;
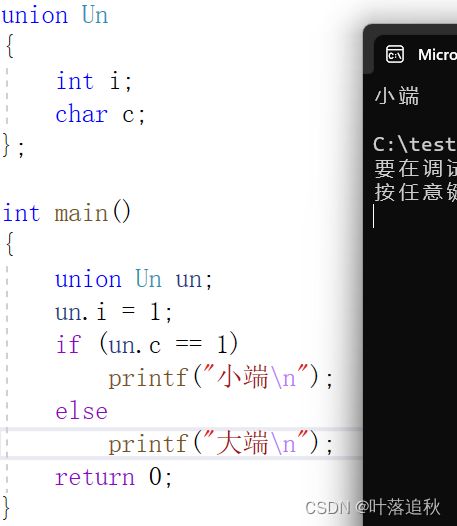
un.i = 1;
if (un.c == 1)
printf("小端\n");
else
printf("大端\n");
return 0;
}
联合体大小的计算
1.联合的大小至少是最大成员的大小。
2.当最大成员大小不是最大对齐数的整数倍的时候,就要对齐到最大对齐数的整数倍。
举例:
//计算联合体的大小
union Un1
{
char c[5];
int i;
};
今天的分享到这里就结束了,觉得不错的朋友们可以三连一波!!!!
追秋在这里再次感谢大家的阅读,我们下次再见!