Leetcode208. 实现Trie（前缀树）C++实现

Leetcode208. 实现Trie（前缀树）

一. 前缀树介绍

1、应用
Trie (发音为 “try”) 或前缀树是一种树数据结构，用于检索字符串数据集中的键。这一高效的数据结构有多种应用：
1）自动补全

2）拼写检查

3）IP路由（最长前缀匹配）

4）九宫格打字预测

5）单词游戏

2、优势
还有其他的数据结构，如平衡树和哈希表，使我们能够在字符串数据集中搜索单词。为什么我们还需要 Trie 树呢？尽管哈希表可以在 O(1)时间内寻找键值，却无法高效的完成以下操作：
找到具有同一前缀的全部键值。
按词典序枚举字符串的数据集。
Trie 树优于哈希表的另一个理由是，随着哈希表大小增加，会出现大量的冲突，时间复杂度可能增加到 O(n)，其中 n 是插入的键的数量。与哈希表相比，Trie 树在存储多个具有相同前缀的键时可以使用较少的空间。此时 Trie 树只需要 O(m) 的时间复杂度，其中 m 为键长。而在平衡树中查找键值需要 O(mlogn) 时间复杂度。

二. Trie树节点结构介绍

Trie 是一颗非典型的多叉树模型，多叉好理解，即每个结点的分支数量可能为多个，其结点具有以下字段：
1）最多 R 个指向子结点的链接，其中每个链接对应字母表数据集中的一个字母。
本文中假定 R 为 26，小写拉丁字母的数量。
2）布尔字段，以指定节点是对应键的结尾还是只是键前缀。、

C++实现：

struct TrieNode {
    bool isEnd; //该结点是否是一个串的结束
    TrieNode* next[26]; //字母映射表
};

这时字母映射表next 的妙用就体现了，TrieNode* next[26]中保存了对当前结点而言下一个可能出现的所有字符的链接，因此我们可以通过一个父结点来预知它所有子结点的值：

for (int i = 0; i < 26; i++) {
    char ch = 'a' + i;
    if (parentNode->next[i] == NULL) {
        说明父结点的后一个字母不可为 ch
    } else {
        说明父结点的后一个字母可以是 ch
    }
}

示例：包含三个单词"sea",“sells”,"she"的 Trie 树

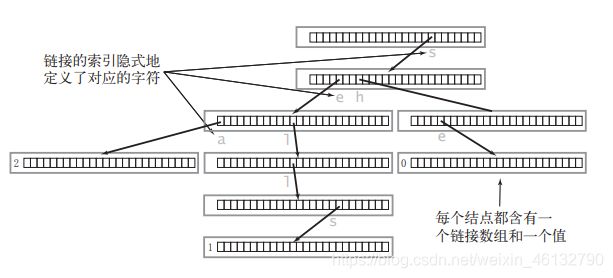
Trie 中一般都含有大量的空链接，因此在绘制一棵单词查找树时一般会忽略空链接，同时为了方便理解我们可以画成这样：

三、Trie树常见操作

3.1 插入

描述：向 Trie 中插入一个单词 word

实现：这个操作和构建链表很像。首先从根结点的子结点开始与 word 第一个字符进行匹配，一直匹配到前缀链上没有对应的字符，这时开始不断开辟新的结点，直到插入完 word 的最后一个字符，同时还要将最后一个结点isEnd = true;，表示它是一个单词的末尾。

    /** Inserts a word into the trie. */
    void insert(string word) {
        Trie* node = this;
        for(char c : word){
            if(node->next[c-'a']==nullptr)node->next[c-'a'] = new Trie();
            node = node->next[c-'a'];
        }
        node->isEnd = true;
    }

3.2 搜索键

描述：查找 Trie 中是否存在单词 word

实现：从根结点的子结点开始，一直向下匹配即可，如果出现结点值为空就返回false，如果匹配到了最后一个字符，那我们只需判断node->isEnd即可。

 /** Returns if the word is in the trie. */
    bool search(string word) {
        Trie* node = this;
        for(char c : word){
            if(node->next[c-'a']==nullptr)return false;
            node = node->next[c-'a'];
        }
        return node->isEnd;
    }

3.3 前缀查找

描述：判断 Trie 中是或有以 prefix 为前缀的单词

实现：和 search 操作类似，只是不需要判断最后一个字符结点的isEnd，因为既然能匹配到最后一个字符，那后面一定有单词是以它为前缀的。

/** Returns if there is any word in the trie that starts with the given prefix. */
    bool startsWith(string prefix) {
        Trie* node = this;
        for(char c : prefix){
            if(node->next[c-'a']==nullptr) return false;
            node = node->next[c-'a'];
        }
        return true;
    }

四、总结

通过以上介绍和代码实现我们可以总结出 Trie 的几点性质：

1、Trie 的形状和单词的插入或删除顺序无关，也就是说对于任意给定的一组单词，Trie 的形状都是唯一的。

2、查找或插入一个长度为 L 的单词，访问 next 数组的次数最多为 L+1，和 Trie 中包含多少个单词无关。

3、Trie 的每个结点中都保留着一个字母表，这是很耗费空间的。如果 Trie 的高度为 n，字母表的大小为 m，最坏的情况是 Trie 中还不存在前缀相同的单词，那空间复杂度就为 O(m^n)。

最后，关于 Trie 希望你能记住 8 个字：一次建树，多次查询。

五、全部代码

class Trie {
private:
    bool isEnd;
    Trie* next[26];
public:
    /** Initialize your data structure here. */
    Trie() {
        isEnd = false;
        memset(next, 0, sizeof(next)); 
    }
    
    /** Inserts a word into the trie. */
    void insert(string word) {
        Trie* node = this;
        for(char c : word){
            if(node->next[c-'a']==nullptr)node->next[c-'a'] = new Trie();
            node = node->next[c-'a'];
        }
        node->isEnd = true;
    }
    
    /** Returns if the word is in the trie. */
    bool search(string word) {
        Trie* node = this;
        for(char c : word){
            if(node->next[c-'a']==nullptr)return false;
            node = node->next[c-'a'];
        }
        return node->isEnd;
    }
    
    /** Returns if there is any word in the trie that starts with the given prefix. */
    bool startsWith(string prefix) {
        Trie* node = this;
        for(char c : prefix){
            if(node->next[c-'a']==nullptr) return false;
            node = node->next[c-'a'];
        }
        return true;
    }
};

/**
 * Your Trie object will be instantiated and called as such:
 * Trie* obj = new Trie();
 * obj->insert(word);
 * bool param_2 = obj->search(word);
 * bool param_3 = obj->startsWith(prefix);
 */

参考链接：
1、https://leetcode-cn.com/problems/implement-trie-prefix-tree/solution/shi-xian-trie-qian-zhui-shu-by-leetcode/
2、https://leetcode-cn.com/problems/implement-trie-prefix-tree/solution/trie-tree-de-shi-xian-gua-he-chu-xue-zhe-by-xiao-x/
若有侵权，联系删帖～