搜索中常见数据结构与算法探究(一)
1 前言
ES现在已经被广泛的使用在日常的搜索中,Lucene作为它的内核值得我们深入研究,比如FST,下面就用两篇分享来介绍一些本文的主题:
- 第一篇主要介绍数据结构和算法基础和分析方法,以及一些常用的典型的数据结构;
- 第二篇主要介绍图论,以及自动机,KMP,FST等算法;
下面开始第一篇
2 引言
“算法是计算机科学领域最重要的基石之一“
“编程语言虽然该学,但是学习计算机算法和理论更重要,因为计算机算法和理论更重要,因为计算机语言和开发平台日新月异,但万变不离其宗的是那些算法和理论,例如数据结构、算法、编译原理、计算机体系结构、关系型数据库原理等等。“——《算法的力量》
2.1 提出问题
2.1.1 案例一
设有一组N个数而要确定其中第k个最大者,我们称之为选择问题。常规的解法如下:
- 该问题的一种解法就是将这N个数读进一个数组中,在通过某种简单的算法,比如冒泡排序法,以递减顺序将数组排序,然后返回位置k上的元素。
- 稍微好一点的算法可以先把前k个元素读入数组并对其排序。接着,将剩下的元素再逐个读入。当新元素被读到时,如果它小于数组中的第k个元素则忽略之,否则就将其放到数组中正确的位置上,同时将数组中的一个元素挤出数组。当算法终止时,位于第k个位置上的元素作为答案返回。
这两种算法编码都很简单,但是我们自然要问:哪个算法更好?哪个算法更重要?还是两个算法都足够好?使用N=30000000和k=15000000进行模拟将发现,两个算法在合理的时间量内均不能结束;每一种算法都需要计算机处理若干时间才能完成。
其实还有很多可以解决这个问题,比如二叉堆,归并算法等等。
2.2.2 案例二
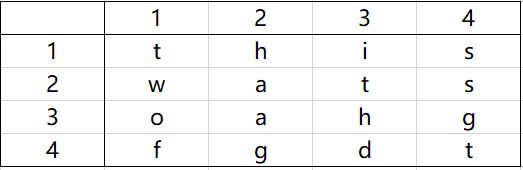
输入是由一些字母构成的一个二维数组以及一组单词组成。目标是要找出字谜中的单词,这些单词可能是水平、垂直、或沿对角线上任何方向放置。下图所示的字谜由单词this、two、fat和that组成。
现在至少也有两种直观的算法来求解这个问题:
- 对单词表中的每个单词,我们检查每一个有序三元组(行,列,方向)验证是否有单词存在。这需要大量嵌套的for循环,但它基本上是直观的算法。
- 对于每一个尚未越出迷板边缘的有序四元组(行,列,方向,字符数)我们可以测试是否所指的单词在单词表中。这也导致使用大量嵌套的for循环。
上述两种方法相对来说都不难编码,但如果增加行和列的数量,则上面提出的两种解法均需要相当长的时间。
以上两个案例中,我们可以看到要写一个工作程序并不够。如果这个程序在巨大的数据集上运行,那么运行时间就变成了重要问题。
那么,使用自动机理论可以快速的解决这个问题,下一篇中给大家详细的分析。
3 数据结构与算法基础
3.1 数据结构基础
3.1.1 什么是数据结构
在计算机领域中,数据是信息的载体,是能够输入到计算机中并且能被计算机识别、存储和处理的符号的总称。数据结构是指数据元素和数据元素之间的相互关系或数据的组织形式。数据元素是数据的的基本单位,数据元素有若干基本项组成。
3.1.2 数据之间的关系
数据之前的关系分为两类:
- 逻辑关系
表示数据之间的抽象关系,按每个元素可能具有的前趋数和直接后继数将逻辑结构分为线性结构和非线性结构。逻辑关系或逻辑结构有如下特点:
- 只是描述数据结构中数据元素之间的联系规律;
- 是从具体问题中抽象出来的数学模型,是独立于计算机存储器的(与硬件无关)
逻辑结构的分类如下:
- 线性结构
- 树形结构
- 图状结构
- 其他结构
2)物理关系
逻辑关系在计算中的具体实现方法,分为顺序存储方法、链式存储方法、索引存储方法、散列存储方法。物理关系或物理结构有如下特点:
- 是数据的逻辑结构在计算机存储其中的映像;
- 存储结构是通过计算机程序来实现,因而是依赖于具体的计算机语言的;
物理结构分类如下:
- 顺序结构
- 链式结构
- 索引结构
3.2 算法基础
3.2.1 基础概念
算法是为求解一个问题需要遵循的、被清楚指定的简单指令的集合。对于一个问题,一旦某种算法给定并且被确定是正确的,那么重要的一步就是确定该算法将需要多少诸如时间或空间等资源量的问题。如果一个问题的求解算法竟然需要长达一年时间,那么这种算法就很难能有什么用处。同样,一个需要若干个GB的内存的算法在当前的大多数机器上也是无法使用的。
3.2.2 数学基础
一般来说,估算算法资源消耗所需的分析是一个理论问题,因此需要一套数学分析法,我们先从数学定义开始。
- 定理1:如果存在正常数c和n0,使得当N>= n0时,T(N) <= cf(N),则记为T(N) = O(f(N))。
- 定理2:如果存在正常数c和n0,使得当N>=n0时,T(N) <= cg(N),则记为T(N) = Ω(g(N))。
- 定理3:T(N) = θ(h(N))当且仅当T(N) = O(h(N)) 和 T(N) = Ω(h(N))。
- 定理4:如果对每一个正常数c都存在常数n0使得当N>n0时,T(N) < cp(N),则T(N) = o(p(N))。
这些定义的目的是要在函数间建立一种相对的级别。给定两个函数,通常存在一些点,在这些点上一个函数的值小于另一个函数的值,因此,一般宣称f(N) 如果用传统的不等式来计算增长率,那么第一个定义T(N) = O(f(N))是说T(N)的增长率小于或者等于f(N)的增长率。第二个定义T(N) = Ω(g(N))是说T(N)增长率大于或者等于g(N)的增长率。第三个定义T(N) = θ(h(N))是说T(N)的增长率等于h(N)的增长率。最后一个定义T(N) = o(p(N))说的则是T(N)的增长率小于p(N)的增长率。他不同于大O,因为大O包含增长率相同的可能性。 要证明某个函数T(N) = O(f(N)) ,通常不是形式的使用这些定义,而是使用一些已知的结果(比如说T(N) = O(log(N)))。一般来说,这就意味着证明是非常简单的计算而不应涉及微积分,除非遇到特殊情况。如下是常见的已知函数结果 在使用已知函数结果时,有几点需要注意: 3.2.3 复杂度函数 正常情况下的复杂度函数包含如下两种: 时间和空间的度量并没有一个固定的标准,但是在正常情况下,时间复杂度的单位基本上是以一次内存访问或者一次IO来决定。空间复杂度是指在算法执行过程中需要占用的存储空间。对于一个算法来说,时间复杂度和空间复杂度往往是相互影响,当追求一个好的时间复杂度时,可能会使空间复杂度变差,即可能占用更多的存储空间;反之,当追求一个较好的空间复杂度时,可能会使时间复杂度变差,即可能占用较长的运算时间。 3.3.1 质数分辨定理(HashTree的理论基础) 简单的说就是,n个不同的质数可以分辨的连续数的个数和他们的乘机相同。分辨是指这些连续的整数不可能有相同的余数序列。 3.3.2 Hash算法 1)Hash 2)常见的Hash算法 3)Hash碰撞 3.3.3 树结构的基本概念 3.3.4 二叉搜索树 二叉搜索树是一棵二叉树,其中每个节点都不能有多于两个子节点。 4.1.1 HashMap 1)总述 2)数据结构和算法 3)优缺点 4)使用场景 4.1.2 Bloom Filter(布隆过滤器) 1)总述 2)数据结构和算法 判断某个key是否在集合时,用k个hash函数算出k个值,并查询数组中对应的比特位,如果所有的bit位都为1,认为在集合中 3)优缺点 4)场景 4.1.3 SkipList(跳表) 1)总述 2)数据结构和算法 有顺序关系的多个Entry(K,V)集合M可以由跳表实现,跳表S由一系列列表{S0,S1,S2,……,Sh}组成,其中h代表的跳表的高度。每个列表Si按照Key顺序存储M项的子集,此外S中的列表满足如下要求: Si中的Entry是从Si-1中的Entry集合中随机选择的,对于Si-1中的每一个Entry,以1/2的概率来决定是否需要拷贝到Si中,我们期望S1有大约n/2个Entry,S2中有大约n/4个Entry,Si中有n/2^i。跳表的高度h大约是logn。从一个列表到下一个列表的Entry数减半并不是跳表的强制要求; 下图为随机数为1的结果图: 删除过程:同查找过程。 时间复杂度 空间复杂度 3)优缺点 4)使用场景 4.2.1 AVL 1)总述 2)数据结构和算法 针对旋转做详细分析如下: 情形1和4是关于a的对称,而2和3是关于a点的对称。因此理论上解决两种情况。 单旋转的简单示意图如下: 双旋转的简单示意图如下: 3)优缺点 4)使用场景 .4.2.2 Red Black Tree 1)总述 2)数据结构和算法 红黑树的示意图如下(图片来源于网络): 那么将一个节点插入到红黑树中,需要执行哪些步骤呢? 在第二步中,被插入的节点被着为红色之后,他会违背哪些特性呢 定理:一棵含有n个节点的红黑树的高度至多为2log(N+1),证明过程请查看参考资料。 3)优缺点 4)使用场景 4.2.3 B+Tree 1)总述 系统从磁盘读取数据到内存时是以磁盘块(block)为基本单位,位于同一块磁盘块中的数据会被一次性读取出来。InnoDB存储引擎中有页(Page)的概念,页是引擎管理磁盘的基本单位。 2)数据结构和算法 B-Tree很适合作为搜索来使用,但是B-Tree有一个缺点就是针对范围查找支持的不太友好,所以才有了B+Tree; 我们将上述特点描述整理成下图(假设一个页(Page)只能写四个数据): 这样的数据结构可以进行两种运算,一种是针对主键的范围查找和分页查找,另外一种是从根节点开始,进行随机查找; 3)优缺点 4)使用场景 4.2.4 HashTree 1)总述 2)数据结构和算法 我们选择质数分辨算法来构建一颗哈希树。选择从2开始的连续质数来构建一个10层的哈希树。第一层节点为根节点,根节点先有2个节点,第二层的每个节点包含3个子节点;以此类推,即每层节点的数据都是连续的质数。对质数进行取余操作得到的数据决定了处理的路径。下面我们以随机插入10个数(442 9041 3460 3164 2997 3663 8250 908 8906 4005)为例,来图解HashTree的插入过程,如下: HashTree的节点查找过程和节点插入过程类似,就是对关键字用质数取余,根据余数确定下一节点的分叉路径,知道找到目标节点。如上图,在从对象中查找所匹配的对象,比较次数不超过10次,也就是说时间复杂度最多是o(1). 删除的过程和查找类似。 3)优缺点: 4.2.5 其他数据结构 鉴于篇幅有限,余下重要数据结构将在下一篇文章中再来一起讨论,敬请期待! 作者:郑冰 潘坤 京东云官网:https://www.jdcloud.com/cn/pages/jinqiucaigou
极限是0:这意味着f(N) = o(g(N))。
极限是c != 0: 这意味着f(N) = θ(g(N))。
极限是∞ :这意味着g(N) = o(f(N))。
极限摆动:二者无关。
时间复杂度
空间复杂度3.3 知识储备
Hash一般翻译成散列,也可以直接音译成哈希,就是把任意长度的输入,通过散列算法变换成固定长度的输出,该输入就是散列值。不同的输入可能散列成相同的值,确定的散列值不可能确定一个输入。
自定义HASH算法:程序设计者可以自定义HASH算法,比如java中重写的hashCode()方法
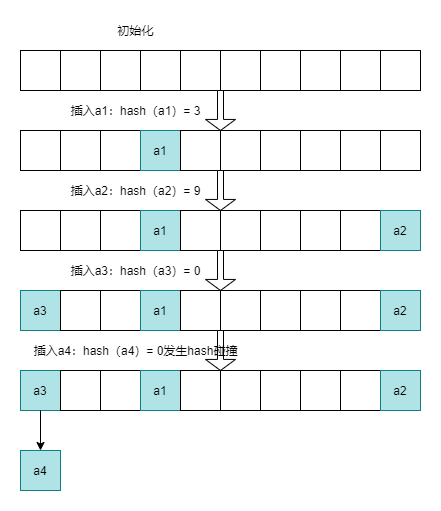
解决Hash碰撞常见的方法有一下几种:
对于二叉查找树的每一个节点X,它的左子树中所有项的值都小于X节点中的项,而它的右子树中所有项的值大于X中的项;4 常见数据结构与算法分析
4.1 线性数据结构
HashMap是开发中最常用的数据结构之一,数据常驻于内存中,对于小的数据量来说,HashMap的增删改查的效率都非常高,复杂度接近于O(1)。
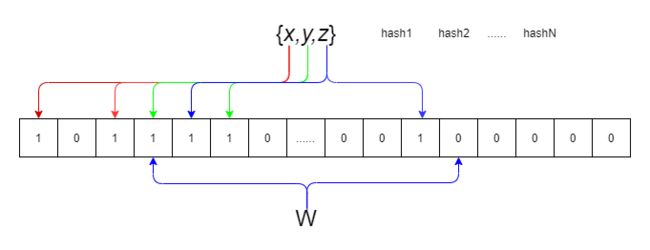
布隆过滤器算法为大数据量的查找提供了快速的方法,时间复杂度为O(k),布隆过滤器的语义为:
布隆过滤器的具体结构和算法为:
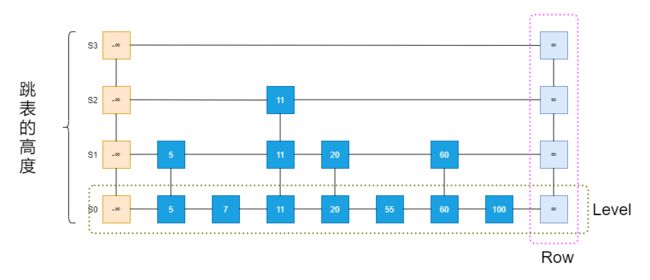
跳表是一种特殊的链表,相比一般的链表有更高的查找效率,可比拟二差查找树,平均期望的插入,查找,删除的时间复杂度都是O(logN);
跳表可视为水平排列(Level)、垂直排列(Row)的位置(Position)的二维集合。每个Level是一个列表Si,每个Row包含存储连续列表中相同Entry的位置,跳表的各个位置可以通过以下方式进行遍历。
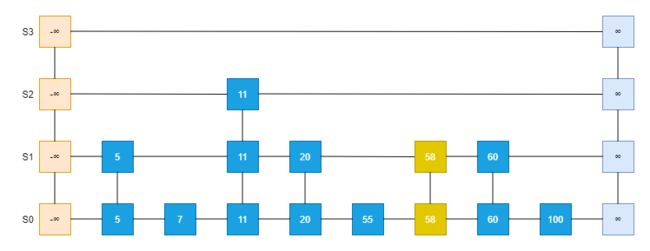
插入的过程描述,以上图为例,插入Entry58:
许多开源的软件都在使用跳表:
4.2 简单非线性数据结构
AVL树是带有平衡条件的二叉查找树,这个平衡条件必须要容易保持,而且它保证树的深度必须是O(logN)。在AVL树中任何节点的两个子树的高度最大差别为1。
AVL树本质上还是一棵二叉查找树,有以下特点:
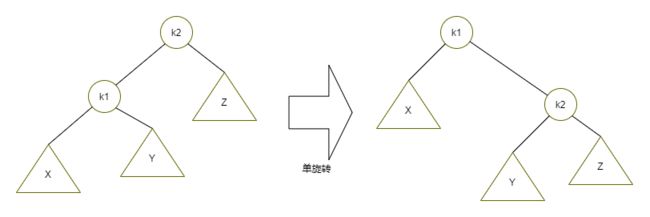
我们把必须重新平衡的节点叫做a,由于任意节点最多有两个儿子,因此出现高度不平衡就需要a点的两棵子树的高度差2。可以看出,这种不平衡可能出现一下四种情况:
第一种情况是插入发生在外侧的情况,该情况通过对树的一次单旋转而完成调整。第二种情况是插入发生在内侧的情况,这种情况通过稍微复杂些的双旋转来处理。
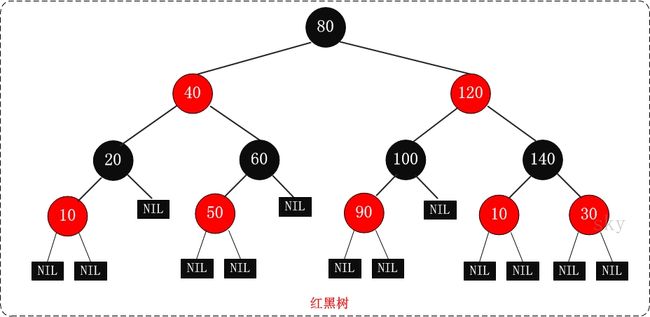
红黑树是一种自平衡的二叉查找树,是2-3-4树的一种等同,它可以在O(logN)内做查找,插入和删除。
在AVL的基础之上,红黑树又增加了如下特点:
由此定理可推论红黑树的时间复杂度为log(N);
提起B+Tree都会想到大名鼎鼎的MySql的InnoDB引擎,该引擎使用的数据结构就是B+Tree。B+Tree是B-Tree(平衡多路查找树)的一种改良,使得更适合实现存储索引结构,也是该篇分享中唯一一个与磁盘有关系的数据结构。首先我们先了解一下磁盘的相关东西。
首先,先了解一下一棵m阶B-Tree的特性:
那么B+Tree的特性在B-Tree的基础上又增加了如下几点:
HashTree是一种特殊的树状结构,根据质数分辨定理,树每层的个数为1、2、3、5、7、11、13、17、19、23、29……
从2起的连续质数,连续10个质数接可以分辨大约6464693230个数,而按照目前CPU的计算水平,100次取余的整数除法操作几乎不算什么难事。