数据架构与算法———B树与B+原理和算法详细介绍(含图解简单易懂)

前言：本篇将讲述B树的具体操作（建树，插入，删除等操作）。动态查找树主要包括：二叉查找树，平衡二叉树，红黑树，B树，B-树，查找的时间复杂度就为O(log2N)，通过对数就可以发现降低树的深度就会提高查找效率。在大数据存储过程，大量的数据会存储到外存磁盘，外存磁盘中读取与写入某数据的时候，首先定位到磁盘中的某一块，这就有个问题：如何才能有效的查找磁盘中的数据呢，这就需要一种高效的外存数据结构，也就引出了下面的课题。

一、B树与B+定义

1.B树定义

（1）一棵m阶的B树，特性如下：

利用书面的定义（参考书籍-《数据结构》）

• 1）树中的每个结点最多含有m个孩子；
• 2）除了根结点和叶子结点，其他结点至少有[ceil(m / 2)（代表是取上限的函数）]个孩子；
• 3）若根结点不是叶子结点时，则至少有两个孩子（除了没有孩子的根结点）
• 4）所有的叶子结点都出现在同一层中，叶子结点不包含任何关键字信息；

（2）B树的类型与节点定义

#define m  1024
struct BTNode;
typedef struct BTNode *PBTNode;
struct BTNode {
    int keyNum;//实际关键字个数，keyNum < m
    PBTNode parent;//指向父亲节点
    PBTNode *ptr;
    keyType *key;//关键字向量
    
}

typedef struct BTNode *BTree;
typedef BTree *PBTree;

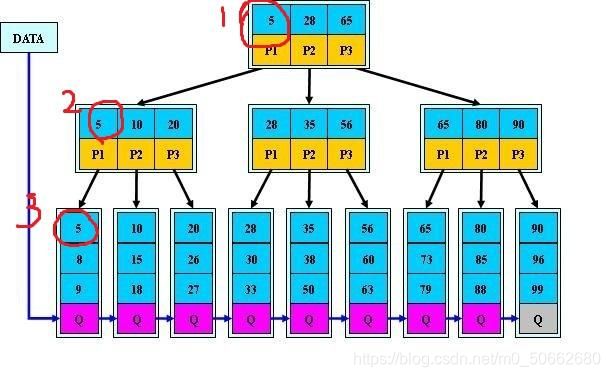
2.B+树定义

B+树可以说是B树的一种变形，它把数据都存储在叶结点，而内部结点只存关键字和孩子指针，因此简化了内部结点的分支因子，B+树遍历也更高效，其中B+树只需所有叶子节点串成链表这样就可以从头到尾遍历，其中内部结点是并不存储信息，而是存储叶子结点的最小值作为索引，下面将讲述到。

定义：参考数据《数据结构》与百度百科

B+树用于数据库和文件系统中，NTFS等都使用B+树作为数据索引，

• 1）有n棵子树的结点含有n个关键字，每个关键字都不会保存数据，只会用来索引，并且所有数据都会保存在叶子结点；
• 2）所有的叶子结点包含所有关键字信息以及指向关键字记录的指针，关键字自小到大顺序连接；

参考下图（来自百度百科）

三、B树与B+问答

1.为什么说B+树比B树更适合做操作系统的数据库索引和文件索引？

（1）B+树的磁盘读写的代价更低

B+树内部结点没有指向关键字具体信息的指针，这样内部结点相对B树更小。

（2）B+树的查询更加的稳定

因为非终端结点并不是最终指向文件内容的结点，仅仅是作为叶子结点中关键字的索引。这样所有的关键字的查找都会走一条从根结点到叶子结点的路径。所有的关键字查询长度都是相同的，查询效率相当。

为了答谢大家关注和支持，这次给大家准备了限时领取福利：阿里面试题、百度面试题、滴滴面试题、华为面试题、京东面试题、美团面试题、腾讯面试题、头条面试题、中兴面试题。

还等什么小编推荐自己的linuxC/C++语言交流群:【1106675687】整理了一些个人觉得比较好的学习书籍、视频资料共享在群文件里面，有需要的可以自行添加哦！前100名进群领取，额外赠送一份价值199的C/C++、linux资料包含(视频教程、电子书、实战项目及代码），下面部分展示。

四、B树与B+树操作

1.B树操作

1.1 B树的插入

B树的插入是指插入一条记录，如果B树已存在需要插入的键值时，用新的值替换旧的值；若B树不存在这个值时，则是在叶子结点进行插入操作。

对高度为h的m阶B树，新结点一般插第h层。通过检索可以确定关键码应插入的位置，

• 1）若该结点中关键码个数小于等于m-1，则直接插入就可
• 2）若该结点中关键码个数等于m-1，则将引起结点的分裂，以中间的关键码为界将结点一分为二，产生了一个新的结点，并将中间关键码插入到父结点中；

重复上述过程，最坏情况一直分裂到根结点， 建立一个新的根结点，整个B树就增加一层。

举例如下：

下面以5阶B树举例，根据B树的定义，结点最多有4个值，最少有2个值。

a）在空树插入39，此时就有一个值，根结点也是叶子结点

b）继续插入22，97和41值，根结点变为4个值，符合要求

c）插入53值

插入之后发现超过结点最多只有4个值，所以要以中间值进行分开，分开后当前结点要指向父结点，分裂之后，发现符合要求

d）插入13，21，40，同样造成分裂，

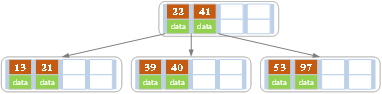
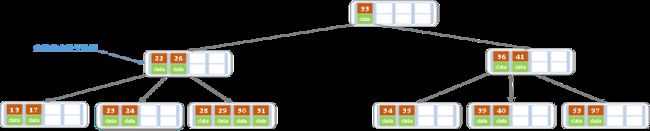
e）紧接着插入30，27，33，36，24，34，35

f）将26再次插入进去

发现有5个值，超过B树的定义，需要以27为中心分裂，27进军父结点

发现父结点也超过4个，再次分裂

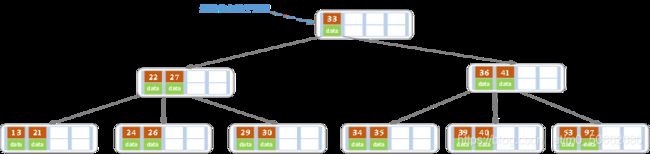
g）最后插入17，28，29，31，32的记录

1.2 B树的删除

B树删除：首先要查找该值是否在B树中存在，如果存在，判断该元素是否存在左右孩子结点，如果有，则上移孩子结点中的相近结点（左孩子最右边的结点或者有孩子最左边的结点）到父结点中，然后根据移动之后的情况；如果没有，进行直接删除；如果不存在对应的值，则删除失败。

• 1）如果当前要删除的值位于非叶子结点，则用后继值覆盖要删除的值，再用后继值所在的分支删除该后继值。（该后继值必须位于叶子结点上）
• 2）该结点值个数不小于Math.ceil(m/2)-1（取上线函数），结束删除操作，否则下一步
• 3）如果兄弟结点值个数大于Math.ceil(m/2)-1，则父结点中下移到该结点，兄弟的一个值上移，删除操作结束。

将父结点的key下移与当前的结点和他的兄弟姐妹结点key合并，形成一个新的结点，有些结点可能有左兄弟，也有右兄弟，我们可以任意选择一个兄弟结点即可。

下面以5阶B树举例进行删除，根据B树的定义，结点最多有4个值，最少有2个值。

a）原始状态

b）在上面的B树删除21，删除之后结点个数大于等于2，所以删除结束

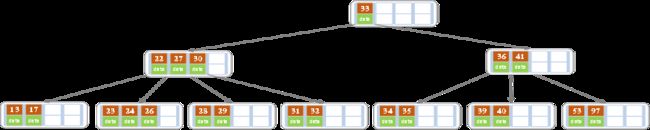
c）删除27之后为

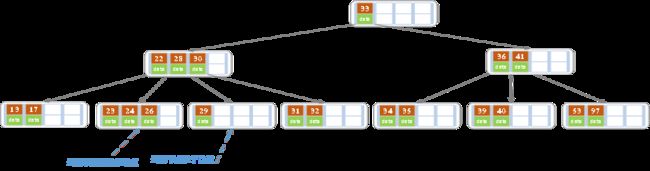
27处于非叶子结点，用27的后继替换。也即是28替换27，然后在右孩子结点删除28，如上。

发现删除，当前叶子结点的记录的个数已经小于2，而兄弟结点中有3个记录我们可以从兄弟结点中借取一个key，父结点中的28就下移，兄弟结点中的26就上移,删除结束，结果如下

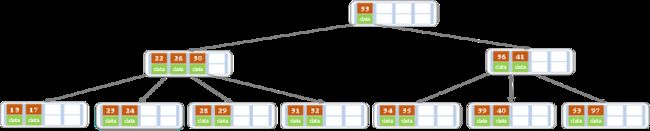
d）删除32

删除之后发现，当前结点中有key，而兄弟都有两个key，所以只能让父结点的30下移到和孩子一起合并，成为新的结点，并指向父结点，经拆封发现符合要求

2.B+树

2.1 B+树的插入

B+树插入：

• 1）若为空树，直接插入，此时也就是根结点
• 2）对于叶子结点：根据key找叶子结点，对叶子结点进行插入操作。插入后，如果当前结点key的个数不大于m-1，则插入就结束。反之将这个叶子结点分成左右两个叶子结点进行操作，左叶子结点包含了前m/2个记录，右结点包含剩下的记录key，将第m/2+1个记录的key进位到父结点中（父结点必须是索引类型结点），进位到父结点中的key左孩子指针向左结点,右孩子指针向右结点。
• 3）针对索引结点：如果当前结点key的个数小于等于m-1，插入结束。反之将这个索引类型结点分成两个索引结点，左索引结点包含前(m-1)/2个数据，右结点包含m-(m-1)/2个数据，然后将第m/2个key父结点中，进位到父结点的key左孩子指向左结点,父结点的key右孩子指向右结点。

下面以5阶B+树举例进行插入，根据B+树的定义，结点最多有4个值，最少有2个值。

a）空树插入5，8，10，15

b）插入16

超过了最大值4，所以分裂，以中间为准

c）插入17，18

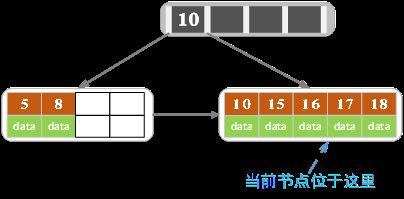
结点的关键字等于5，大于4，进行分裂。

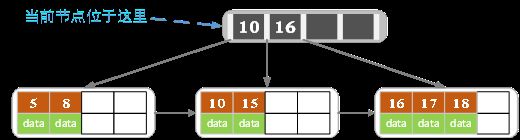
符合条件，插入完成。

2.2 B+树删除

面以5阶B+树举例进行删除，根据B+树的定义，结点最多有4个值，最少有2个值。

下面是初始状态

a）删除22，删除后个数为2，删除结束

b）删除15，结果如下：

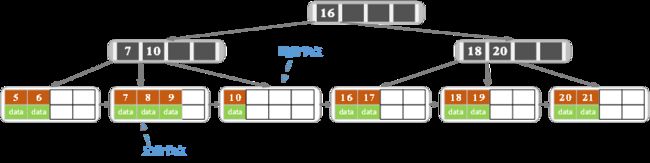
删除之后，只有一个值，而兄弟有三个值，所以从兄弟结点借一个关键字，并更新索引结点

大家可以考虑删除7.我在这里直接给出结果

以上就是B树和B+树的操作，建议大家拿支笔操作一下，毕竟提高能力是没有错的。

五、代码实现

//测试程序1  
#include   
#include   
#include   
#include "BTree.h"  
using namespace std;  
  
int main()  
{     
    char iKey[] = {'C','N','G','A','H','E','K','Q','M','F','W','L','T','Z','D','P','R','X','Y','S'};  
    char dKey[] = {'C','N','G','A','H','E','K','Q','M','F','W','L','T','Z','D','P','R','X','Y','S'};  
    int iSize = sizeof(iKey)/sizeof(char);  
    int dSize = sizeof(dKey)/sizeof(char);  
  
    int i;  
    BTree<char> btree(5, NULL);     
    cout<<"----------插入测试----------"<<endl;  
    for(i = 0; i < iSize; i++) //插入测试  
    {  
        cout<<"插入"<<iKey[i]<<"以后"<<endl;  
        btree.Insert(iKey[i]);  
        btree.PrintBTree();  
    }  
    cout<<"----------删除测试----------"<<endl;  
    for(i = 0; i < dSize; i++) //删除测试  
    {  
        cout<<"删除"<<dKey[i]<<"以后"<<endl;  
        btree.Delete(dKey[i]);  
        btree.PrintBTree();  
    }  
    return 0;  
}

//测试程序2  
#include   
#include   
#include   
#include "BTree.h"  
using namespace std;  
  
int main()  
{     
    srand((int)time(0));  
    const int iSize = 100000;  //插入次数   
    const int dSize = 100000;  //删除次数  
    const int num = 100;       //测试组数  
    int *iKey = new int[iSize];  
    int *dKey = new int[dSize];   
    int i, j;  
    for(j = 0; j < num; j++)  //测试组数，每次测试都是插入iSize次，删除dSize次  
    {  
        for(i = 0; i < iSize; i++)  //插入数据生成  
            iKey[i] = rand()%iSize;  
        for(i = 0; i < dSize; i++)  
            dKey[i] = rand()%iSize; //删除数据生成  
  
        int m = rand()%400 + 3;  //随机生成3阶到402阶  
        BTree<int> btree(m, NULL);      
        cout<<"----------第"<<j<<"组插入测试----------"<<endl;  
        for(i = 0; i < iSize; i++) //插入测试  
            btree.Insert(iKey[i]);  
        cout<<"第"<<j<<"组插入测试成功，为"<<m<<"阶B树"<<endl;  
        cout<<"----------第"<<j<<"组删除测试----------"<<endl;  
        for(i = 0; i < dSize; i++) //删除测试  
            btree.Delete(dKey[i]);  
        cout<<"第"<<j<<"组删除测试成功，为"<<m<<"阶B树"<<endl<<endl;  
    }  
    delete [] iKey;  
    delete [] dKey;  
    return 0;  
}  

1 //BTree.h文件，由于使用了模板所以没法将声明与实现分离  
  2 #pragma once  
  3 #include <queue>  
  4 using namespace std;  
  5   
  6 //B树的结点定义  
  7 template <typename T>  
  8 struct BTreeNode  
  9 {  
 10     int num;               //关键字个数    
 11     T *K;                  //指向关键字数组  
 12     BTreeNode<T> *parent;  //指向父亲结点  
 13     BTreeNode<T> **A;      //指向孩子结点数组的指针  
 14     BTreeNode(int n, int m, BTreeNode<T>  *p)  
 15     {  
 16         num = n;  
 17         parent = p;  
 18         K = new T[m+1];           //最多有m-1个关键字，K0不用，Km用来当哨兵  
 19         A = new BTreeNode *[m+1]; //最多有m个分支，Am用来当哨兵  
 20         for(int i = 0; i <= m; i++)  
 21             A[i] = NULL;  
 22     }  
 23     ~BTreeNode()  
 24     {  
 25         delete [] K; K = NULL;    
 26         delete [] A; A = NULL;  
 27     }  
 28 };  
 29   
 30 //搜索结果的三元组定义  
 31 template <typename T>  
 32 struct Triple  
 33 {  
 34     BTreeNode<T> * node;  //关键字所在结点  
 35     int i;                //关键字下标位置  
 36     bool tag;             //搜索是否成功  
 37     Triple(BTreeNode<T> *nd, int pos, bool t)   
 38     { node = nd; i = pos; tag = t;}  
 39 };  
 40   
 41 //B树定义  
 42 template <typename T>  
 43 class BTree  
 44 {  
 45 public:  
 46     BTree();  
 47     BTree(int m , BTreeNode<T> * root);  
 48     ~BTree();  
 49     Triple<T> Search(const T& x); //搜索核心函数  
 50     bool Insert(const T& x);      //插入核心函数  
 51     bool Delete(const T& x);      //删除核心函数  
 52     void InsertKey(BTreeNode<T> *p, T k, BTreeNode<T> *a, int i);    //插入一个二元组(K,A)  
 53     void SpliteNode(BTreeNode<T> *p, T *k, BTreeNode<T> **a, int i); //分裂结点  
 54     void RightAdjust(BTreeNode<T> *p, BTreeNode<T> *q, int i);  //从右子女取关键字  
 55     void LeftAdjust(BTreeNode<T> *p, BTreeNode<T> *q, int i);   //从左子女取关键字  
 56     void LeftCompress(BTreeNode<T> *p, int i);  //往左移动1个位置  
 57     void RightCompress(BTreeNode<T> *p, int i); //往右移动1个位置  
 58     void MergeNode(BTreeNode<T> *p, BTreeNode<T> *q, BTreeNode<T> *pR, int i); //合并两个结点  
 59     void PrintBTree(); //打印B树  
 60 private:  
 61     int m_m;                //路数，即最大子树棵数  
 62     BTreeNode<T> *m_pRoot;  //B树的根结点  
 63 };  
 64 template<typename T>  
 65 BTree<T>::BTree() //默认构造函数  
 66 {  
 67     m_m = 5;         //默认是5阶  
 68     m_pRoot = NULL;  //根结点初始为空  
 69 }  
 70 template<typename T>  
 71 BTree<T>::BTree(int m , BTreeNode<T> * root)  
 72 {  
 73     m_m = m;        
 74     m_pRoot = root;  
 75 }  
 76 template<typename T>  
 77 BTree<T>::~BTree() //释放所有的空间  
 78 {  
 79     if(m_pRoot != NULL)  
 80     {  
 81         queue<BTreeNode<T> *> nodeQueue; //利用队列，按层次遍历B树  
 82         nodeQueue.push(m_pRoot);         //放入根结点  
 83         while(nodeQueue.size())  
 84         {  
 85             BTreeNode<T> * p = nodeQueue.front();  
 86             if(p->A[0] != NULL) //不是叶结点，需考虑子女结点的删除  
 87             {  
 88                 for(int i = 0; i <= p->num; i++)  
 89                     nodeQueue.push(p->A[i]);  
 90             }  
 91             nodeQueue.pop();  
 92             delete p;  
 93             p = NULL;  
 94         }  
 95     }  
 96 }  
 97 //函数功能： 查找关键字x是否在B树中  
 98 //函数参数： x为查找的关键字  
 99 //返回值：   一个Triple对象(node, i, tag)，tag=true表示x等于结点r中的Ki；tag=false表示x不在树中，r是最后一个被搜索的结点  
100 template <typename T>  
101 Triple<T> BTree<T>::Search(const T &x)  
102 {  
103     int i = 0;  //下标  
104     BTreeNode<T> *p = m_pRoot, *q = NULL;  //用来保存当前结点和它的父结点  
105   
106     while(p != NULL) //一直检查到叶结点  
107     {  
108         //n, A0,(K1, A1), (K2, A2), ... (Kn, An)  
109         //确定i，使得Ki <= x < Ki+1，K[0]不放数据  
110         //下面这条语句当然也可以写成 for(i = 1; i <= n && x >= p->K[i]; i++)  
111         //但是为了与Ki <= x < Ki+1这个关系式统一，采用了下述写法，观察后面的程序，发现这样写还避免了下标溢出的判断   
112         int n = p->num;   //当前结点的关键字个数     
113         for(i = 0; i < n && x >= p->K[i+1]; i++)  //可以改进一下，用二分查找  
114             ;  
115         if(x == p->K[i]) //是否已找到，不用判断下标，i最大为n   
116             return Triple<T>(p, i, true);  
117         q = p;  
118         p = p->A[i];     //搜索下一层，Ki与Ki+1中间的指针  
119     }  
120     return Triple<T>(q, i, false); //x不在树中，找到了可以插入的结点位置  
121 }  
122 //函数功能： 插入关键字x到B树中  
123 //函数参数： x为插入的关键字  
124 //返回值：   插入是否成功  
125 template <typename T>  
126 bool BTree<T>::Insert(const T &x)  
127 {  
128     if(m_pRoot == NULL) //空树  
129     {  
130         m_pRoot = new BTreeNode<T>(1, m_m, NULL);  //新的根含有1个关键字  
131         m_pRoot->K[1] = x;    //根的关键字  
132         return true;  
133     }  
134   
135     Triple<T> triple = Search(x);     //检查是否已存在  
136     if(triple.tag == true) //x已在B树中  
137         return false;  
138   
139     BTreeNode<T> *p = triple.node, *q; //结点地址  
140     //构造插入的两元组(k,a) 其中k为关键字，a为右邻指针  
141     BTreeNode<T> *a = NULL;  
142     T k  = x;  
143     int i = triple.i;   
144   
145     while(1) //插入过程  
146     {  
147         if(p->num < m_m-1) //关键字个数未到达上限，可以直接插入  
148         {  
149             InsertKey(p, k, a, i); //(k, a)插入到位置(Ki, Ai)后面  
150             return true;  
151         }  
152         SpliteNode(p, &k, &a, i); //将p结点分裂成两个结点，一个结点仍为p，另外一个变为两元组(k,a)，以便插入到父结点  
153         if(p->parent != NULL)     //父结点不为空  
154         {  
155             q = p->parent; //获得父结点  
156             for(i = 0; i < q->num && x >= q->K[i+1]; i++) //确定新的插入位置i  
157                 ;  
158             p = q;   //进入上一层  
159         }  
160         else  
161         {  
162             //已经到达了根，需要新建一个结点  
163             m_pRoot = new BTreeNode<T>(1, m_m, NULL);  //新的根含有1个关键字  
164             m_pRoot->K[1] = k; //新根的关键字  
165             m_pRoot->A[0] = p; //左指针  
166             m_pRoot->A[1] = a; //右指针  
167             p->parent = a->parent = m_pRoot; //更新左右指针的父结点  
168             return true;  
169         }  
170     }  
171 }  
172 //函数功能： 插入关键字x到B树中，这是实际的插入函数  
173 //函数参数： p指向插入关键字所在结点，k为插入的关键字，a为关键字的右邻，i为插入位置  
174 //返回值：   无  
175 template <typename T>  
176 void BTree<T>::InsertKey(BTreeNode<T> *p, T k, BTreeNode<T> *a, int i)  
177 {  
178     for(int j = p->num; j > i; j--) //将K[i],A[i]以后的元素都往后移一个位置  
179     {  
180         p->K[j + 1] = p->K[j];  
181         p->A[j + 1] = p->A[j];  
182     }  
183     p->num++;        //结点的关键字个数加1  
184     p->K[i + 1] = k; //插入两元组在K[i],A[i]以后  
185     p->A[i + 1] = a;  
186     if(a != NULL)    //若为为空，需更新父结点指针  
187         a->parent = p;  
188 }  
189 //函数功能： 分裂结点  
190 //函数参数： p指向要分裂的结点，k指向插入的关键字，a指向关键字的右邻，i为插入位置  
191 //返回值：   无  
192 template <typename T>  
193 void BTree<T>::SpliteNode(BTreeNode<T> *p, T *k, BTreeNode<T> **a, int i)  
194 {  
195     InsertKey(p, *k, *a, i); //先插了再说  
196     int mid = (m_m + 1)/2;   //[ceil(m/2)]  
197     int size = (m_m & 1)? mid : mid + 1; //奇偶性决定了分裂时拷贝的关键字个数  
198   
199     BTreeNode<T> *q = new BTreeNode<T>(0, m_m, p->parent); //新结点  
200     //将p的K[mid+1...m]和A[mid..m]移到q的K[1...mid-1]和A[0...mid-1]  
201     q->A[0] = p->A[mid];  
202     for(int j = 1; j < size; j++)  
203     {  
204         q->K[j] = p->K[mid + j];    
205         q->A[j] = p->A[mid + j];    
206     }  
207     //修改q中的子女的父结点为q，这里很重要，因为这些子女原来的父结点为p  
208     if(q->A[0] != NULL)  
209     {     
210         for(int j = 0; j < size; j++)  
211             q->A[j]->parent = q;  
212     }  
213     //更新结点的关键字个数  
214     q->num = m_m - mid;  //结点q：m –[ceil(m/2)], A[ceil(m/2)],(K [ceil(m/2)]+1, A [ceil(m/2)]+1), …, (Km, Am)  
215     p->num = mid - 1;    //结点p：[ceil(m/2)]–1, A0, (K1, A1), (K2,A2), …, (K[ceil(m/2)]–1, A[ceil(m/2)]–1)   
216     //构建新的两元组(k,a)  
217     *k = p->K[mid];  
218     *a = q;  
219 }  
220   
221 //函数功能： 删除关键字x  
222 //函数参数： x为要删除的关键字  
223 //返回值：   删除是否成功  
224 template <typename T>  
225 bool BTree<T>::Delete(const T& x)  
226 {  
227     Triple<T> triple = Search(x); //检查是否已存在  
228     if(triple.tag == false)       //x不在B树中  
229         return false;  
230     BTreeNode<T> *p = triple.node, *q; //要删除的关键字所在结点  
231     int i = triple.i;  
232   
233     if(p->A[i] != NULL) //非叶结点  
234     {  
235         q = p->A[i];    //找右子树的最小关键码  
236         while(q->A[0] != NULL)  
237             q = q->A[0];  
238         p->K[i] = q->K[1];   //用叶结点替换  
239         LeftCompress(q, 1);  //删除K[1]，其实只是用后面的结点覆盖一下即可  
240         p = q;               //转换为叶结点的删除  
241     }  
242     else  
243         LeftCompress(p, i);  //叶结点直接删除，其实只是用后面的结点覆盖一下即可  
244   
245     int mid = (m_m + 1) / 2; //求[ceil(m/2)]  
246     //下面开始调整  
247     while(1)  
248     {  
249         if(p == m_pRoot || p->num >= mid-1) //情形1和情形2  
250             break;  
251         else  
252         {  
253             q = p->parent; //父亲结点  
254             for(i = 0; i <= q->num && q->A[i] != p; i++) //找到p在父结点中的位置Ai  
255                 ;  
256             if(i == 0)     //p为最左指针  
257                 RightAdjust(p, q, i);  //结点p、父结点q、p的右兄弟结点进行旋转调整  
258             else  
259                 LeftAdjust(p, q, i);   //结点p、父结点q、p的左兄弟结点进行旋转调整  
260             p = q;         //向上调整  
261         }  
262     }  
263     if(m_pRoot->num == 0) //一颗空树  
264     {  
265         p = m_pRoot->A[0];  
266         delete m_pRoot;  
267         m_pRoot = p;  
268         if(m_pRoot != NULL)  
269             m_pRoot->parent = NULL;  
270     }  
271     return true;  
272 }  
273 //函数功能： 通过右子女调整，如果右子女有多余结点，从右子女取一个关键字  
274 //函数参数： p指向被删除的关键字所在结点，q指向父结点，i为p在q中的位置  
275 //返回值：   无  
276 template <typename T>  
277 void BTree<T>::RightAdjust(BTreeNode<T> *p, BTreeNode<T> *q, int i)  
278 {  
279     BTreeNode<T> *pR = q->A[i+1];  //p的右兄弟  
280     if(pR->num >= (m_m+1)/2)       //情形3，兄弟有足够多的关键字，即至少还有[ceil(m/2)]  
281     {  
282         //调整p  
283         p->num++;                  //p的关键字个数加1  
284         p->K[p->num] = q->K[i+1];  //父结点相应关键码下移  
285         p->A[p->num] = pR->A[0];   //右兄弟最左指针移到p的最右  
286         if(p->A[p->num] != NULL)  
287             p->A[p->num]->parent = p;  //修改父结点，原来是pR  
288         //调整父结点  
289         q->K[i+1] = pR->K[1];      //右兄弟的最小关键码上移到父结点  
290         //调整右兄弟  
291         pR->A[0] = pR->A[1];       //右兄弟剩余关键字与指针前移  
292         LeftCompress(pR, 1);       //覆盖K[1],A[1]，关键字个数减1，LeftCompress中自动会减1    
293     }  
294     else  
295         MergeNode(p, q, pR, i + 1);//情形4 (...p Ki+1 pR...)  
296 }  
297 //函数功能： 通过左子女调整，如果左子女有多余结点，从左子女取一个关键字  
298 //函数参数： p指向被删除的关键字所在结点，q指向父结点，i为p在q中的位置  
299 //返回值：   无  
300 template <typename T>  
301 void BTree<T>::LeftAdjust(BTreeNode<T> *p, BTreeNode<T> *q, int i)  
302 {  
303     BTreeNode<T> *pL = q->A[i-1]; //p的左兄弟  
304     if(pL->num >= (m_m+1)/2)      //情形3  
305     {  
306         //调整p  
307         RightCompress(p, 1);     //p的关键字和指针往右移动，空出位置放左子女的关键字，RightCompress会自动加1  
308         p->A[1] = p->A[0];     
309         p->K[1] = q->K[i];        //父结点相应关键码下移  
310         p->A[0] = pL->A[pL->num]; //左兄弟最右指针移到p的最左  
311         if(p->A[0] != NULL)  
312             p->A[0]->parent = p;      //修改父结点，原来是pL  
313         //调整父结点  
314         q->K[i] = pL->K[pL->num]; //左兄弟的最大关键码上移到父结点  
315         //调整左兄弟  
316         pL->num--;   //左兄弟的关键字个数减1  
317     }  
318     else  
319     {  
320         //左右互换一下，以符合合并函数的参数要求  
321         BTreeNode<T> *pR = p;  
322         p = pL;  
323         MergeNode(p, q, pR, i);   //情形4，注意这里i，而不是i+1 (...p Ki pR...)  
324     }  
325 }  
326 //函数功能： 将结点p自i+1开始的关键字和指针往左移动1，原来的K[i],A[i]其实被覆盖掉了  
327 //函数参数： p指向结点，i为被覆盖的位置  
328 //返回值：   无  
329 template <typename T>  
330 void BTree<T>::LeftCompress(BTreeNode<T> *p, int i)  
331 {  
332     int n = p->num;   //结点关键字个数  
333     for(int j = i; j < n; j++)  
334     {  
335         p->K[j] = p->K[j + 1];  
336         p->A[j] = p->A[j + 1];  
337     }  
338     p->num--; //关键字个数减1  
339 }  
340 //函数功能： 将结点p自i开始的关键字和指针往右移动1，原来的K[i],A[i]空出来了  
341 //函数参数： p指向结点，i为空出来的位置，用于放新的关键字  
342 //返回值：   无  
343 template <typename T>  
344 void BTree<T>::RightCompress(BTreeNode<T> *p, int i)  
345 {  
346     for(int j = p->num; j >= i; j--) //K[i],A[i]空出来用以放插入的二元组  
347     {  
348         p->K[j + 1] = p->K[j];  
349         p->A[j + 1] = p->A[j];  
350     }  
351     p->num++; //关键字个数加1  
352 }  
353 //函数功能： 合并两个结点  
354 //函数参数： p指向结点，q指向父亲，pR指向p的右兄弟，i为(...p,K,pR...)中的K位置  
355 //返回值：   无  
356 template <typename T>  
357 void BTree<T>::MergeNode(BTreeNode<T> *p, BTreeNode<T> *q, BTreeNode<T> *pR, int i)  
358 {  
359     int n = p->num + 1;   //p结点下一个放关键字的位置  
360     p->K[n] = q->K[i];    //下降父结点的关键字  
361     p->A[n] = pR->A[0];   //从右兄弟左移一个指针  
362     for(int j = 1; j <= pR->num; j++) //将右兄弟剩余关键字和指针移到p中  
363     {  
364         p->K[n + j] = pR->K[j];  
365         p->A[n + j] = pR->A[j];  
366     }  
367     if(p->A[0]) //修改p中的子女的父结点为p，这里很重要，因为这些子女原来的父结点为pR，与分裂相对  
368     {  
369         for(int j = 0; j <= pR->num; j++)  
370             p->A[n + j]->parent = p;  
371     }  
372     LeftCompress(q, i);            //父结点的关键字个数减1  
373     p->num = p->num + pR->num + 1; //合并后关键字的个数  
374     delete pR;  
375     pR = NULL;  
376 }  
377 //函数功能： 打印B树  
378 //函数参数： 无  
379 //返回值：   无  
380 template <typename T>  
381 void BTree<T>::PrintBTree()  
382 {  
383     if(m_pRoot != NULL)  
384     {  
385         queue<BTreeNode<T> *> nodeQueue; //利用队列  
386         nodeQueue.push(m_pRoot);         //放入根结点  
387         while(nodeQueue.size())  
388         {  
389             BTreeNode<T> * p = nodeQueue.front();  
390             if(p->A[0] != NULL) //非叶结点  
391             {  
392                 nodeQueue.push(p->A[0]);  //将子女结点的指针放入队列中  
393                 for(int i = 1; i <= p->num; i++)  
394                 {  
395                     nodeQueue.push(p->A[i]);  
396                     cout<<p->K[i]<<' ';  
397                 }  
398             }  
399             else  
400             {  
401                 for(int i = 1; i <= p->num; i++)  
402                     cout<<p->K[i]<<' ';  
403             }     
404   
405             if(p->parent) //打印父结点的第一个关键字  
406                 cout<<"-----First key of their parent:"<<p->parent->K[1]<<endl;  
407             else  
408                 cout<<endl;  
409             nodeQueue.pop();  
410         }  
411     }  
412 } 

可以直接运行，大家可以复制粘贴进行效果查看（算法思想很重要）

上面就是B树和B+树从概念到代码应用，B树从数据库引出的，讲完之后，也会重回数据库。下一篇将继续讲解针对SQLite进行封装的FMDB第三方的讲解并附带项目中实际使用。

欢迎大家指正。