哈工大2020秋算法设计与分析大作业(一)
哈工大2020秋算法设计与分析大作业(一)
- 前言
- 正文
-
- 1 论文题目
-
- 标题
- 作者
- 刊物
- 2 论文阅读报告
-
- 2.1 摘要
- 2.2 问题定义
- 2.3 算法或证明过程
- 2.4 实验结论
哈工大2020秋算法设计与分析大作业(二)
前言
本课程以前是考试课,在我们这一届变成了考察课。2020秋季学期情况比较特殊,由于疫情原因提前放假,所以期末考试也相应提前,最后因为时间太紧,老师取消了这门课的期末考试,采取阅读论文提交报告的形式,占期末分数的100%。正常情况下大作业40%,期末考试60%。本人期末得分95,教学班排名第三。
正文
1 论文题目
标题
Effective and Efficient Community Search over Large Heterogeneous Information Networks
作者
Yixiang Fang, Yixing Yang, Wenjie Zhang, Xuemin Lin, Xin Cao University of New South Wales, Australia
[email protected], [email protected]
[email protected], [email protected], [email protected]
刊物
2020年2月VLDB(第13卷,第6期)
http://dl-acm-org-s.i.hit.edu.cn:1080/doi/10.14778/3380750.3380756
2 论文阅读报告
2.1 摘要
最近,社区搜索(CS)相关的话题得到了广泛的关注。给定查询顶点,CS将搜索包含该值的密集子图。现有的研究主要侧重于搜索同一类型的同质图形,不能直接应用于由多图形、互联对象(如书目网络和知识图)组成的异构信息网络(HIN)。本文对大型HIN的社区搜索问题进行研究;也就是说,给定一个查询顶点q,从包含q的HIN中查找一个社区,其中所有顶点都具有相同类型的q并且具有密切的联系。
为了对同一类型的两个顶点之间的关系进行建模,我们采用众所周知的元路径概念,它是在不同类型顶点之间定义的一系列关系。然后,我们使用元路径扩展经典的最低度量值,从而衡量社区的凝聚力。我们还提出了使用这些凝聚力指标查找社区的高效查询算法。我们对五个真正的大型HIN进行了广泛的实验,结果表明,我们提出的解决方案对搜索社区是有效的。此外,它们比基线解决方案快得多。
2.2 问题定义
- 定义1. HIN . HIN是有向图G =(V,E),它具有顶点型映射函数ψ:V→A和边型映射函数φ:E→R,其中每个顶点v∈V所属对于一个顶点类型ψ(v)∈A,每边e∈E都属于边型(也称关系)φ(e)∈R。
- 定义2. HIN模式 . 给定一个HIN图G =(V,E)有着对于ψ:V→A和φ:E→R的映射,其模式为TG,是定义在顶点类型A和边类型R上的有向图,即TG =(A,R)。HIN模式描述了顶点之间所有允许的边类型,每个边类型可以描述一对一,一对多,或者多对多的关系。图1(b)显示了DBLP网络的模式,其中标记为“A”、“P”、“V”和“T”的顶点分别表示作者、论文、地点和主题。请注意,如果顶点类型A到顶点类型B之间有一条边R,则边R^(−1)从B到A自然存在。
- 定义3. 元路径 . 元路径P是在HIN模式TG =(A,R)上定义的路径,并且表示为

模式,式中,l是P的长度,Ai∈A,Ri∈R(1≤i≤l)。
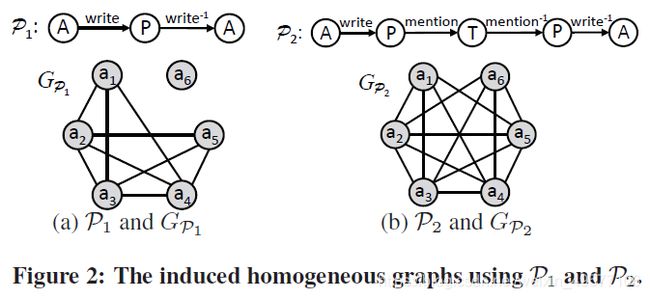
如果同一对顶点类型之间不存在多条边,我们还使用顶点类型名称来表示元路径,即P =(A1A2···Al+1)。如果P’是TG中P的反向路径,我们称之为元路径P的反向元路径,并用P(−1)表示。如果P与P(−1)相同,我们就称P是对称的。例如,元路径P1(图2(a))可以写成P1=(APA)。因为它的反向元路径仍然是P1,所以它是对称元路径。
我们称顶点a1和al+1之间的路径p=a1→a2····→al+1为P的路径实例,如果对于∀i,顶点ai和边ei=(ai,ai+1)满足ψ(ai)=Ai和φ(ei)=Ri。例如,在图1(a)中,路径a1→p1→a2是P1的路径实例。在这里,我们使用小写字母(如a1)表示HIN中的顶点,使用大写字母(如A)表示顶点类型。我们说一个顶点u是一个顶点v的P-近邻,当它们可以通过P的一个实例连接。如果存在一个从u到v的顶点链,使得任何顶点都是链中相邻顶点的P-近邻,我们说两个顶点u和v是P-连通的。
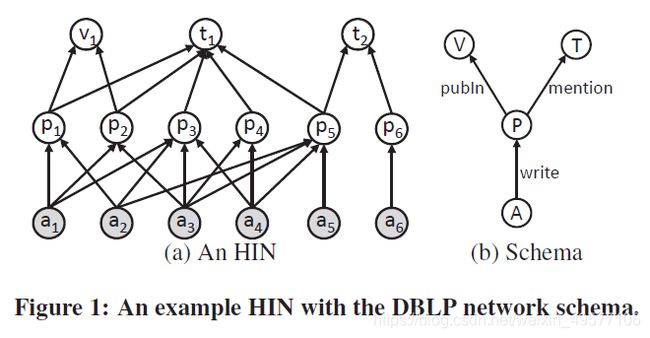
为了描述社区的凝聚力,现有的研究成果经常使用k核。给定一个齐次图H和一个整数k(k>0),k核是H的最大子图,用Hk表示,使得每个顶点在Hk内都有k次或更多次。例如,在图2(a)中,1核、2核和3核包含顶点{a1,···,a5}。
- 问题定义
本文的目的是从一个包含查询顶点q的HIN中寻找一个社区,其中所有的顶点都是ψ(q)型的,也称为目标型。从概念上讲,社区中的顶点应该紧密相连。为了将顶点和目标类型连接起来,我们采用了一个对称的元路径P,其起始和结束类型都是目标类型。为了刻画内聚性,我们通过引入对称元路径P将经典的k-核扩展为(k,P)-核。注意,本文后面提到的所有元路径都是对称的;对于非对称元路径,我们可以用类似的方式扩展有向图的核模型。
设P是连接两个顶点和目标类型的元路径。给定一个顶点v和一个目标类型的顶点集S,我们定义α(v,S),称为基本度或b度,作为v在集S内的P-近邻的个数。基于b度的概念,我们介绍基本(k,P)-核模型。
- 定义4. 基本(k,P)-核 . 给定一个HIN G和一个整数k,G的基本(k,P)-核是P连通顶点的极大集Bk,p ,s.t.∀v∈Bk,p ,α(v,Bk,p)≥k,其中Bk,p的顶点是P连通的类型。
综上所述,由于许多路径实例可能共享相同的边,因此基本(k,P)核可以包含在核中弱接合的顶点。为了解决这个问题,我们开发了新的基于不相交路径的核心模型。具体地说,考虑一个具有目标类型的顶点v,设Ψ[v]是P的一组从v开始的路径实例。我们说Ψ[v]是一组边不相交的路径,如果对于任意两个路径实例p1,p2∈Ψ[v],它们的第i条(1≤i≤l)边是不同的,第(l+1)个顶点是不同的。同样地,我们说Ψ[v]是一组顶点不相交的路径,如果对于任意两个路径实例p1,p2∈Ψ[v],它们的第i个(2≤i≤l+1)顶点是不同的。请注意,两条边或顶点不相交的路径可能共享相同的边或顶点,这些边或顶点将位于这两条路径的不同位置。
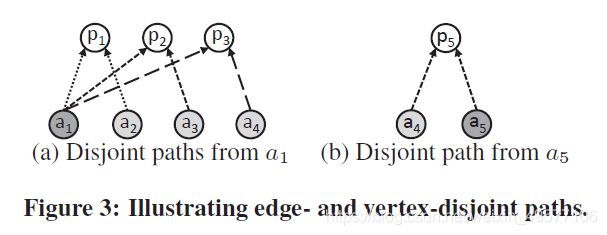
一个顶点通常包含在多组边不相交或顶点不相交的路径中。在本文中,我们考虑最大集,并用β(v,S)(resp.,γ(v,S))表示从顶点v开始到集S顶点的边不相交(resp.,顶点不相交)路径实例的最大数目。为了简单起见,我们称β(v,S)(resp.,γ(v,S))为v的e阶(resp.,v阶)。在图1(a)中,设v=a1和S={a1,·······,a6}。如果P=(APA),则β(a1,S)=γ(a1,S)=3,其中边和顶点不相交路径的最大集合如图3(a)所示。类似地,如果P=(APTPA),那么我们有β(a1,S)=3和γ(a1,S)=1。
- 定义5. 边不相交(k,P)-核。给定一个HIN G和一个整数k,G的边不相交(k,P)-核是P-连通顶点s.t. ∀v∈Ek,p ,β(v,Ek,p)≥k的极大集,其中Ek,p的顶点是由P连接的类型。
- 定义6. 顶点不相交(k,P)-核。给定一个HIN G和一个整数k,G的顶点不相交(k,P)-核是P-连通顶点s.t. v∈Vk,p ,γ(v,Vk,p)≥k的极大集,其中Vk,p的顶点是由P连接的类型。
在没有歧义的上下文中,我们把Bk,p,Ek,p和Vk,p分别写成Bk,Ek和Vk。我们说一个顶点v有一个核数k,如果它是最大的k,那么有一个对应的(k,P)-核包含v。换句话说,(k,P)-核的每个顶点必须有一个对应的核数k或更多。
例1。考虑图1(a),让P =(APA)。对于基本(k,P)-核,Bk={a1,···,a5},其中1≤k≤3。对于边点(k,P)-核,E1={a1,···,a5},E2=E3={a1,a2,a3,a4}。对于顶点不相交(k,P)-核,Vk=Ek,其中1≤k≤3。没有B4、E4或V4。我们以作者a5为例来说明核心数字。在基本核模型、边不相交核模型和顶点不相交核模型下,其核数分别为3、1和1。
现在我们正式介绍CSH问题如下。 - 问题1。给定一个HING G、一个查询顶点q、一个对称元路径P、一个整数k(k>0)和一个特定的(k,P)-核模型,返回包含q的相应(k,P)-核。
在例1中,设q=a1,P=(APA),k=3。如果我们指定基本(k,P)-核作为社区模型,我们得到一个社区B3;如果采用边和顶点不相交(k,P)-核,我们可以分别得到社区E3和V3。显然,由于任何(k,P)-核都是P-连通顶点的极大集,因此该社区满足结构极大性和连通性的性质。
2.3 算法或证明过程
在这一节中,我们将为CSH问题开发有效的算法。特别地,对于每个核心模型,我们开发了一个基本算法和一个高级算法。虽然基本算法简单明了,但正如我们的实验所示,它们不如高级算法有效。我们在表4中总结了所有高级算法,其中越多意味着更高的内聚性,ni是P中第i个顶点类型的顶点数,di,i+1是与P中第i个顶点类型的顶点相连的(i+1)个顶点类型的最大顶点数,σ2

- 基本(k,P)核算法
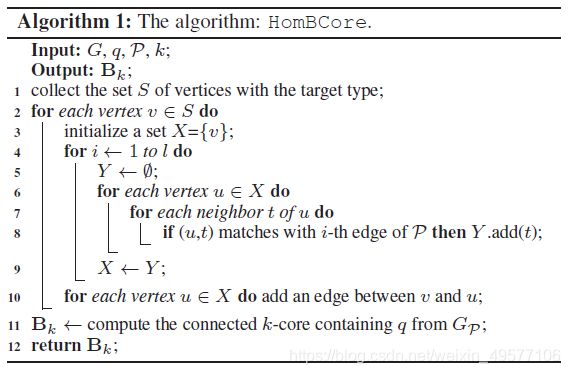
一个基本算法是先构造一个诱导齐次图GP,然后从GP中返回包含q的连通k核。具体来说,它包括三个步骤:(1)收集目标类型的所有顶点的集合;(2)对于每个顶点v∈S,枚举从v开始的P的所有路径实例的集合Ψ[v],并使用Ψ[v]在v与其每个P-邻域之间添加一条边;(3)找到包含q的连通k-核。然而,该算法对于大HINs上的长元路径由于在步骤(2)中,Ψ[v]的大小可能是指数大的,即O(n^l),其中n是P中顶点类型的最大顶点数,l是P的长度。为了加快步骤(2),我们提出了一种批量搜索策略。我们没有枚举所有的路径实例,而是将P分解为一个边列表,并以批量处理的方式为每个边找到匹配的顶点。我们称改进的算法为HomBCore,如算法1所示。我们首先找到S(第1行)。然后,对于每个顶点v(第2-3行),我们初始化一个集合X,通过批量查找与P的每个边匹配的顶点(第4-9行)来获取其P-邻居。最后,我们从GP(第10-12行)计算Bk。
- 改进后的(k,P)核算法
HomBCore的主要局限性在于它必须为目标类型的所有顶点建立一个诱导齐次图GP。然而,这是昂贵和不必要的,因为(1)并非所有具有目标类型的顶点都P-连接到q;(2)它为每个具有目标类型的顶点找到所有P-邻居。为了解决这两个问题,我们提出了两种标签策略,即带标签的批量搜索和带标签的深度优先搜索。

带标签的批量搜索(BSL)。BSL策略是基于HomBCore中的批搜索算法,但带有标签。例如,在图1(a)中,让q=a1和P=(APA)。通过使用BSL,我们将找到五位作者{a1,···,a5}。注意,作者a6被排除在外,因为它不是P连接到a1的。算法2(第1-11行)给出了BSL的详细步骤。具体地说,我们首先使用批搜索找到q的P-邻域集。在这个过程中,每当我们发现一条边(v,u)与P的第i条边匹配时,如果它没有标号i,我们就给它加上标号i并把u加到Y上;如果它有标号i,我们就直接跳过它。请注意,最初,边没有标签。在找到Y之后,我们在下一次迭代中找到新的顶点,它们是Y中顶点的P-邻居。重复此过程,直到所有顶点都被标记。很明显,当我们使用标签时,每一条边都是以恒定的时间访问的。因此,寻找一组P-连接到q的顶点需要线性时间开销,该时间开销以
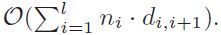
为界。
带标签的深度优先搜索(DSL)。根据定义,Bk只要求其每个顶点至少有k个P-近邻。同时,如现有的CS研究所示,k通常不是很大。基于这种观察,我们建议动态地为每个顶点保持k个P-邻域。具体来说,我们首先为每个顶点找到最多k个P-邻域,然后迭代删除不满足k约束的顶点。由于删除顶点v将删除v的P-邻域顶点的P-邻域,因此我们需要为v的P-邻域增量提供新的P-邻域。为了逐步找到这些P-邻居,我们提出了DSL策略。具体地说,在使用深度优先搜索找到路径p之后,我们检查p的每个顶点,并将其标记为“已访问”,前提是之前已经考虑了它的所有邻居。例如,考虑图4中v=a1和P=(APTPA)的HIN。在找到路径a1→p1→t1→p4→a2和路径1→p1→t1→p4→a3之后,我们将把a2、a3和p4标记为已访问。在查找剩余路径时,将不考虑这些标记的顶点。这样可以确保每次访问每个边的次数不变。因此,对于每个顶点,枚举其所有路径实例需要时间。
首先,我们使用BSL策略来寻找一组P-连接到q的所有顶点(第1-11行)。然后,它为

每个顶点找到最多k个路径实例,并将没有k个路径的顶点收集到队列Q中(第12-14行)。然后,它迭代地从Q中删除顶点v,检查每个P-近邻u,删除从u到v的路径,尝试找到一条从u开始到S中某个顶点结束的新路径,如果存在,则将其添加到Ψ[u];否则,将v添加到Q(第15-24行)。在循环之后,S中的每个顶点都有k个P-邻居。
注意,由于每个顶点只找到k个P-邻域,因此我们无法使用这些P-邻域找到P-连通的最大顶点集。例如,在图1(a)中,设q=a1,k=2,P=(APTPA)。在为每个顶点找到两个P-邻域之后,我们可以得到两个断开的组件,如图5所示,其中每个边表示一个路径实例。为了解决这个问题,我们重新使用BSL策略来寻找S和P-连接到q的顶点的最大集合Bk,在此过程中,所有具有目标类型的顶点都被限制在S中。
- 引理2. FastBCore的总时间成本为

- 边不相交(k,P)-核算法
(1)一种基于延迟剥离的算法
受k核计算的剥离范式的启发,我们提出了一种通过迭代删除β(v,S)值小于k的顶点来计算Ek的算法,其中S最初包含所有具有目标类型的顶点。删除顶点v后,我们需要减少β(u,S),其中u是v的P-近邻。然而,减少β(u,S)的步骤是不平凡的,因为它可能保持不变。例如,考虑图6(a)中的HIN,v=a1,S={a1,a2,a3}。首先,我们得到β(a1,S)=1。去掉a2或a3后,β(a1,S)=1。为了解决这一问题,一种简单的方法是通过精确计算v的每个P-近邻u的β(u,S)。然而,这是非常昂贵的,因为P-邻居的数量是巨大的,并且运行精确也是昂贵的。为了缓解这一问题,我们提出了一种延迟剥离策略,通过一个关键的观察来尽可能延迟精确的运行-在去除v之后,β(u,S)最多减少1。具体地说,对于每个顶点v∈S,我们首先使用贪婪算法计算一个近似β(v,S)。然后,我们维护一个队列来保持当前β(v,S)值小于k的顶点。每当我们将顶点v出列时,我们使用exact计算β(v,S)的精确值。然后,如果β(v,S)
基于以上讨论,我们开发了一个算法,用LazyECore表示,如算法3所示。首先,根据定理1,由于Ek⊆Bk,它计算Bk(第1行)。然后,它初始化队列Q和数组b[],以保持β(v,S)(第2行)。接下来,它使用贪心法计算β(v,S),如果β(v,S)
- 推论1. 给定一个HIN,一个顶点v和一组目标类型的顶点S,如果贪心算法最多不能找到kl路径实例,则得到β(v,S)
- 引理4. LazyECore在

时间内完成,其中σ1(σ1
(2) 一种基于批量剥离的算法
在这一节中,我们开发了另一个算法,它借用了FastBCore的思想,并以批处理的方式删除了核心数小于k的顶点。我们用BatchECore表示它。回想一下,FastBCore按顺序删除不在Bk中的顶点,在此期间,我们动态地为每个顶点维护一组k路径实例。由于贪心算法能够增量地找到边不相交的路径实例,因此我们还可以动态地为每个顶点维护一组k条边不相交的路径。此外,本文提出了一种批量剥离策略,以代替逐点剥离。具体地说,每当我们找到一组不在Ek中的顶点时,我们移除它的所有顶点,并以一种集体的方式更新它们的P-邻域的β(v,S)值。与逐个剥离相比,它节省了大量计算成本,因为对于β(v,S)值接近k的顶点,经常调用Exact。请注意,批剥离不能用于LazyECore,因为在调用Exact之前,它无法确定是否删除顶点。对于HomBCore,批剥离也不能提高效率,因为移除顶点v后,它会枚举v的P-邻域,并在需要时提供新的路径实例,因此我们不在HomBCore中使用批剥离。算法4给出了BatchECore。首先,它收集所有通过BSL P连接到q的顶点,并初始化一个集合T和一个数组Ψ[](第1-2行)。然后,对于每个顶点v∈S,通过贪心(第3-4行)找到一组至多k条边不相交的路径Ψ[v]。根据推论1,如果|Ψ[v]|
- 引理5. BatchECore在
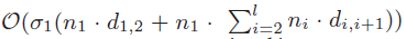
时间内完成,其中σ1(σ1 - 引理4. LazyECore在
- 顶点不相交(k,P)-核算法
在本节中,我们重点讨论计算Vk。与Ek类似,我们不能直接从诱导齐次图中计算Vk,因此我们必须迭代地移除没有足够顶点不相交路径的顶点。接下来,我们首先讨论如何计算γ(v,S),然后说明计算Ek的算法可以很容易地适用于计算Vk。为了计算γ(v,S),我们扩展了精确算法和贪婪近似算法。对于Exact,我们通过在Exact中稍微修改流网络来构建一个新的流网络。具体地说,在EBuilder建立了一个流网络F=(VF,EF)之后,对于源顶点和汇顶点之间的每个中间顶点g∈F,我们把它分成两个顶点,比如g+和g-,这样g的边连接到g+,g-连接到外边,g+与g-相连,其容量设置为1。用VBuilder表示这种流网的构造方法。很容易观察到γ(v,S)等于修正网络中最大流量的容量。

我们用例子5来说明这一点。重新考虑示例3,其中EBuilder构建的流网络如图7(b)所示。通过VBuilder,我们可以得到一个新的流动网络,如图8所示,γ(a1,S)=3。回想一下贪婪迭代地寻找P的路径实例,在找到路径实例P之后,它移除P的所有边。为了计算γ(v,S),我们可以遵循相同的步骤,但是将移除所有边的步骤替换为移除所有顶点。显然,该算法仍能达到1/l的近似比。
为了计算Vk,我们扩展了LazyECore和BatchECore,将计算β(v,S)的步骤简单地替换为计算γ(v,S)。我们分别用LazyVCore和BatchVCore表示扩展算法。不难看出,它们的时间复杂度最多分别是LazyECore和BatchECore的c(c≤4)倍,因为VBuilder构建的流动网络最多是EBuilder的两倍,精确需要O(| EF | ^2/l)时间。

- 基于索引的算法
为了建立核心索引,我们为每个元路径P∈∧创建一个graphHP,然后连接HP的邻接列表。算法5给出了步骤。我们首先计算每个顶点的核数,也称为核分解,并得到顶点列表(按核数降序排列)(第3-4行)。然后,对于每个顶点v’,我们创建一个节点v。然后,我们找到一组v’的P近邻,对于每个顶点U’,如果没有从节点v到节点U的路径,我们创建一条边(v,U)(第4-9行)。注意,为了检查节点之间的连接,我们使用标准的union-find数据结构,其中MAKESET创建一个节点,find查找一个节点的根,union使两个节点具有相同的根。上述索引构建方法依赖于核心分解的关键步骤(第3行)。为此,我们在第3节中扩展了在线算法。对于核心模型下的特定元路径P,我们递增地计算所有(k,P)-核心,其中k从0增加到其最大值。注意,一旦我们计算了所有的(k,P)-核,我们就可以通过利用它们的嵌套关系从这些(k,P)-核计算(k+1,P)-核。

- 引理7. 给定一组∧元路径和一个核模型,算法5取
 时间,其中Δi是Pi的核分解代价,ti是由Pi连接的类型的顶点数,di是第i个顶点类型的最大P邻域数,α(ti)是逆阿克曼函数(小于5)对于ti的所有实际值)。
时间,其中Δi是Pi的核分解代价,ti是由Pi连接的类型的顶点数,di是第i个顶点类型的最大P邻域数,α(ti)是逆阿克曼函数(小于5)对于ti的所有实际值)。 - 证明. 给定一个元路径Pi,调用FIND,UNION,MAKESET函数最多需要O(α(ti))时间。对于每对Pi连通顶点,我们只调用FIND和UNION常数倍,所以需要O(ti·di·α(ti)),引理7成立。
2.4 实验结论
- 在线算法。图15显示了通过改变k得到的在线算法的效率结果。如图15(a)-15(e)所示,FastBCore始终比HomBCore快,因为对于具有目标类型的每个顶点,HomBCore会找到它的所有p近邻,而FastBCore只找到其中的一小部分。同时,k越大,FastBCore的运行时间越长,因为k越大意味着找到更多的P-邻居。HomBCore的运行时间几乎保持稳定,因为主要开销来自于构造齐次图。从图15(f)-15(j)中,我们可以看到BatchECore始终比LazyECore快。这是因为在BatchECore中调用Exact的总次数通常比在LazyECore中小得多,即σ2<σ1。例如,在正方形上,σ1平均大于σ2一个数量级。同时,随着k值的增加,BatchECore的运行时间略有增加,LazyECore的运行时间略有减少。这是因为随着k变大,BatchECore需要为目标类型的顶点找到更多的路径实例,而LazyVECore也需要找到更多的路径实例,但运行精确计算β(v,S)的成本更低,使得总时间变得更小。

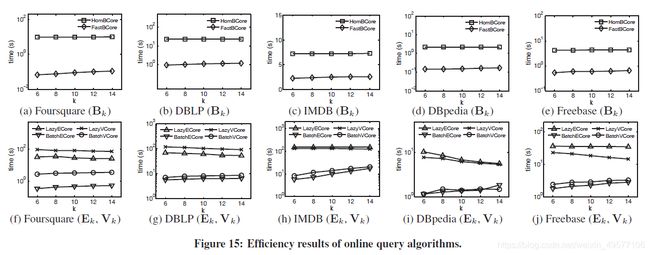
同样,对于Vk,我们可以观察到这样的趋势。此外,很容易观察到查询Bk花费的时间最少,而计算Vk花费的时间最多。主要原因是计算k顶点不相交路径比寻找不需要满足这种约束的k条路径要昂贵。 - 可扩展性测试。对于每个数据集,我们随机选择20%、40%、60%、80%和100%的顶点,分别得到由这些顶点诱导的五个子图。然后,我们对每个核心模型使用高级算法运行在线CSH查询,并在图16中报告效率结果。我们可以看到,通常情况下,它们会随着顶点的数量而扩展。此外,它们的性能趋势与前面讨论的类似。
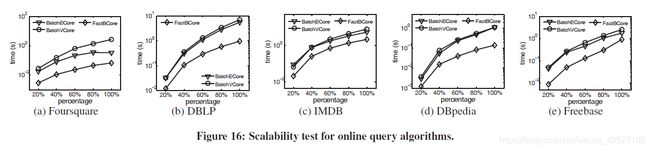
- 核心分解。每个在线查询算法都可以扩展为核心分解。然而,对于基本core模型,FastBCore和HomBCore都需要找到每个顶点的所有P-邻域,而FastBCore需要额外的代价来动态维护k个P-邻域,因此HomBCore是一个更好的选择,我们跳过了FastBCore。对于每个数据集,我们使用这五种算法,并在图17中报告每个元路径的核心分解的平均时间开销。显然,分解Bk需要最少的时间成本,因为它的核心模型比其他模型简单。BatchECore在分解Ek方面始终比LazyBCore快,同样,BatchVCore也比LazyBCore快。另一个有趣的观察是,在几乎所有的数据集上,Vk可以比Ek更有效地分解(使用它们更快的算法,即BatchECore和BatchVCore)。这主要是因为这两种方法都是从k=0开始逐步分解核心,但Vk的最大核心数小于Ek的最大核心数,所以BatchVCore在核心分解上花费的时间较少。

- 指标建设。为了构建CoreIndex,我们对三个核心模型HomBCore、BatchECore和BatchVCore使用了更快的核心分解算法。对于每个数据集,我们考虑表5中的所有元路径,并在图18中报告效率结果。一般来说,构造索引的时间开销与核心分解的时间开销是一致的,即为Bk构造corefindex所花费的时间开销最小,Vk的时间开销小于Ek。原因是,给定每个顶点的核心数,构建核心索引的压缩图几乎需要线性时间开销。
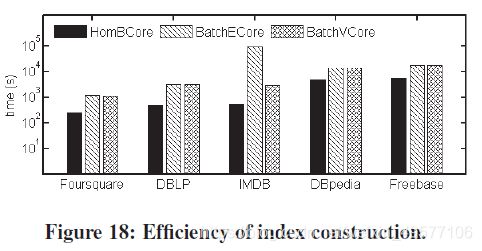
- 基于索引的查询。图19显示了基于索引的查询的效率结果。显然,基于索引的查询算法比在线查询算法快3到5个数量级,因为它们需要最佳的查询时间开销。另外,查询Vk最快,查询Ek比查询Bk快,因为定理1中|Vk|≤|Ek|≤|Vk|。
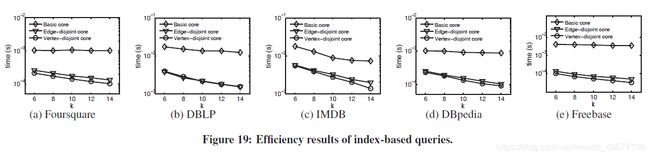
本文研究了CSH问题,其目的是寻找HIN中查询顶点的社区。对具有相同类型顶点的社区建立凝聚力模型,采用著名的元路径概念并提出了三种核心通过合并元路径进行建模。对于每个核心模型,我们开发高效的在线查询算法。此外,我们还开发了一个压缩索引结构,进一步提高查询效率。我们的实验结果表明,所提出的方法在大型HIN上搜索社区是很有效的。

