简单多边形内的最短路径树算法

前言

本文主要介绍<< Linear-time algorithms for visibility and shortest path problems inside simple polygons >>中计算多边形内所有顶点距离多边形内一点的最短路径树的线性算法

字母定义

简单多边形 $P$
顶点个数 $n$
给定的源点 $s$

对于$P$中的每个顶点 $v$
$\pi (s,v)$表示从s到v的最短欧几里得距离路径

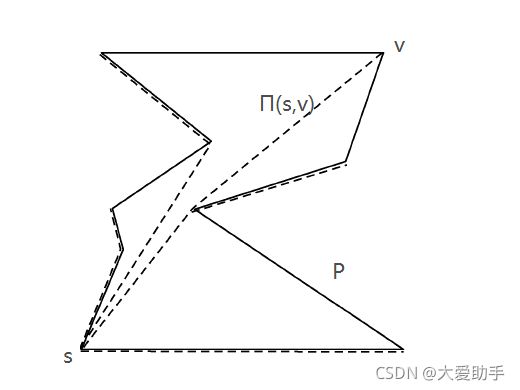
$Q_{sp}$表示所有$\pi (s,v)$的并集,也叫$P$的最短路径树(shortest path tree)

$G$表示$P$内的三角剖分
$T$表示$G$的对偶图

令$d=uw$表示$P$中的一个对角线或边
令$a$表示$u$和$w$在$Q_{sp}$中的最近共同祖先
$F=F_{uw}=\pi (a,w)\cup \pi (a,w)$表示对于$uw$的通道,$a$为该通道的尖点(cusp)

性质

$\pi (s,u)$和$\pi (s,w)$都是外凸(outward convex)

算法准备

计算多边形$P$的三角剖分 ($O(n)$)

维持一个通道$F=F_{uw}=[u_l,u_{l-1},...,a,w_1,...,w_k]$,其中$a=u_0=w_0$表示$F$的尖点,$\pi (a,v)=[u_0,...,u_{l-1}],\pi (a,w)=[w_0,...,w_k]$,$u_{l-1}=u,w_k=w$

$F$存储在 finger tree中,可以$O(log\delta )$的时间内搜索到元素x,也可以$O(log\delta )$的时间内在元素x处分开两颗子树($\delta$表示$x$到最近finger的距离).维持一个指向a的指针$CUSP(F)$.

算法从s和相邻顶点$v_1$开始,$CUSP(F)=s$.

算法

令$u$和$w$为$F$的第一个和最后一个元素,$a=CUSP(F)$.
令$\Delta uwx$为$G$中以$uw$为边且未被处理的唯一三角形

1. 在$F$中二分搜索$v$,满足$vx$与$F$相切,若没有,则$v=a$.
   将$F\cup \{x\}$划分为通道$F_1=[u,...,v,x]和F_2=[x,v,...,w]$
   若$v$属于$\pi (a,u)$,则$CUSP(F_1)=v,CUSP(F_2)=a$
   否则,$CUSP(F_1)=a,CUSP(F_2)=v$
2. 令$\pi (s,x)=\pi (s,v)\cup vx$,只需将$x$的返回指针指向$v$
3. 如果$ux$是对角线,继续Algorithm($F_1$).如果wx是对角线,继续Algorithm($F_1$).