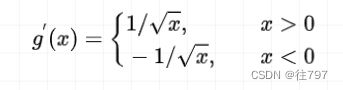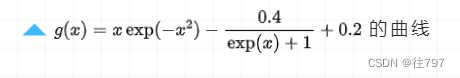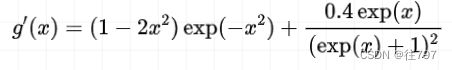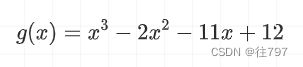牛顿法+++
1.上篇
牛顿法的雏形就是「求平方根」。
1.1何谓平方根倒数速算法
特别地，牛顿法在「计算平方根的倒数」应用领域也是相当的广泛，也就是求解函数：
比如在计算机图形学领域中，相关图像匹配需要计算结果的归一化，这时就要对整个矩阵的每个元素求平方根倒数。
1.2如何用牛顿法求函数零点
一、例题讲解
先看个小例子：
这个函数是一个5次多项式的，比起大家熟悉的二次多项式复杂多了。
令g(x) = 0 ，就能得到一个方程，如何求解这个方程的根呢，「也就是函数的零点怎么求？
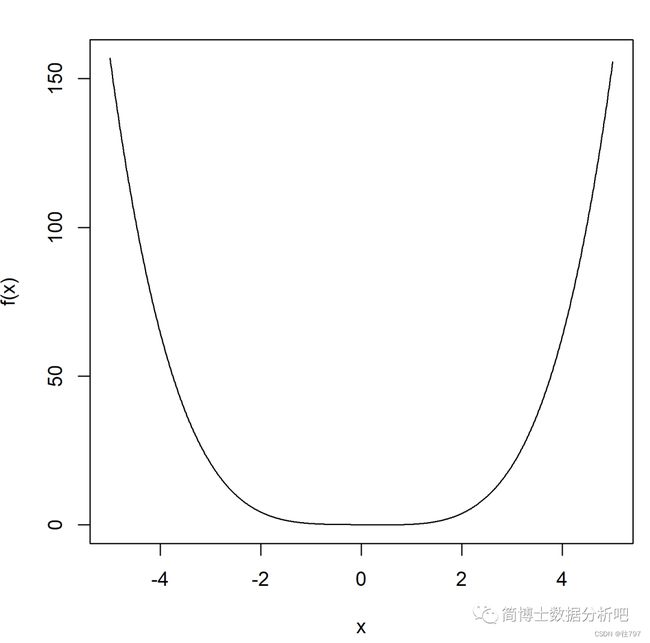
▲5次函数曲线
先来个直观感受，把曲线画出来，零点貌似就在区间 [0, 1] 上。
不妨再取个放大镜来，凑近了看看这个零点。
可以发现，零点好像在 [0.6, 0.8] 之间，我们之前知道了迭代的思想，也就是说不妨先取一个初始值，然后我们之后用迭代公式进行迭代，那么这一次我们取什么样的初始值呢？
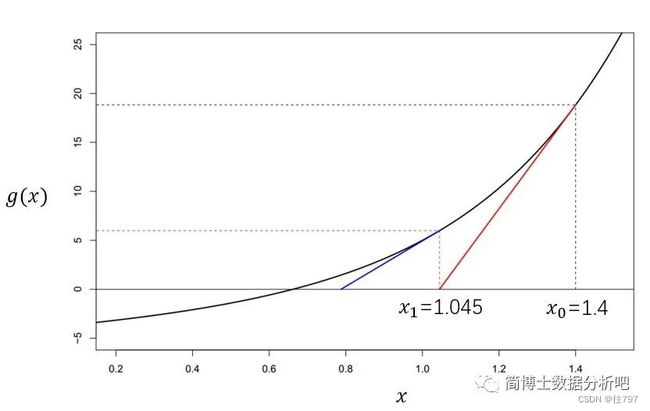
为了方便演示，我们并没有取一个特别接近的，因为那样看起来大家可能就觉得效果不明显，我们取一个比较大的值，「令 
」。
▲求 时的函数值
初始值现在就选取了 ，将这个值带入到我们的函数中。看一下所得的函数值是多少？「g（
）=18.8」
这个值可是相当的大，距离零点挺遥远的，这就是我们最初所在的初始值了。
没关系，路漫漫其修远兮，吾将上下而求索！
即使最初猜的有可能是错误的，但是希望我们绕来绕去总能找到真理。
▲沿着 的点画切线与x轴相交
好了，接着往下找，怎么找下一个点？现在沿着 这个点做一下这个曲线的切线，也就是图中「红色的切线」，这个点处的切线与 x 轴有了一个新的交点，那么可以将新的交点记作下一个迭代值 ，它等于多少？「
」。
▲ 时的函数值
显而易见，通过它的函数值 「g（
）=6」，我们发现， 好像距离 g（x）=0 近了些
▲沿着 的点画切线与x轴相交
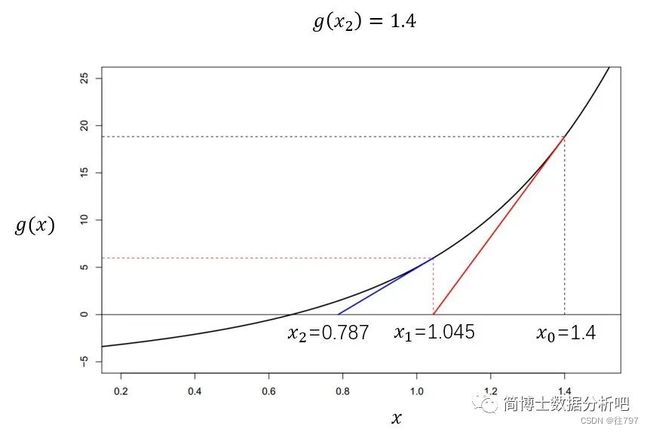
继续采用同样的方法寻找下一个点，当然是沿着曲线做切线，也就是我们所得到「蓝色的切线」，然后就又找到了一个与 x 轴的交点，这个交点不妨记作 
。
▲
时的函数值
可以看到 所对应的函数值更小了，比我们刚才那个 g（）=6 还要小，更接近于 0，于是我们更加有信心了，加油！
▲
时的函数值
接着求索下一个迭代点，因为已经轻车熟路了，很快就求出来 ， 所对应的函数值为 g（
）=2，这一次可是距离零点更接近了，突然觉得很欣慰，好像我们离真理的确不远了，「不停地重复下去，最终就能够找到我们想要的那个零点」。
这里，我们设定迭代阈值 
，展示了整个迭代过程。
▲求解5次多项式函数的迭代结果
最终求到的零点为
。
这个迭代点怎么求出来的呢？回顾之前整个过程，每次都是「在相应的点处求切线，然后找到切线与 x轴 的交点」，所以关键点有两个。
二、迭代原理解读
来看一下迭代原理的「3步走」。
三、使用牛顿法求零点时的各种小bug
案例1：
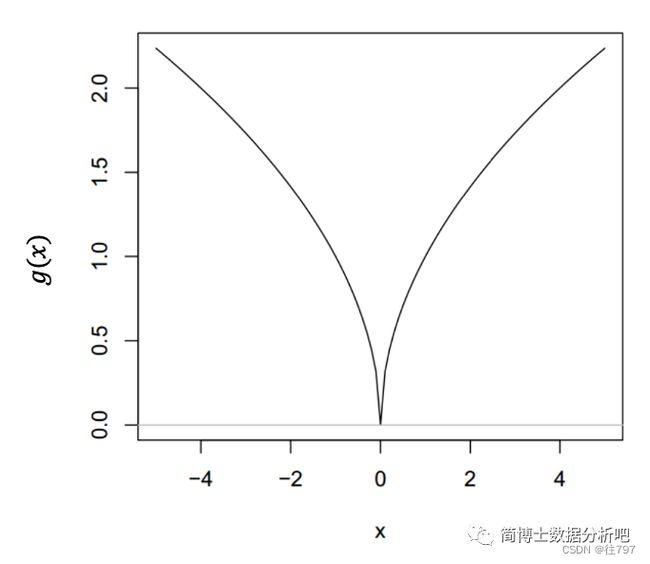
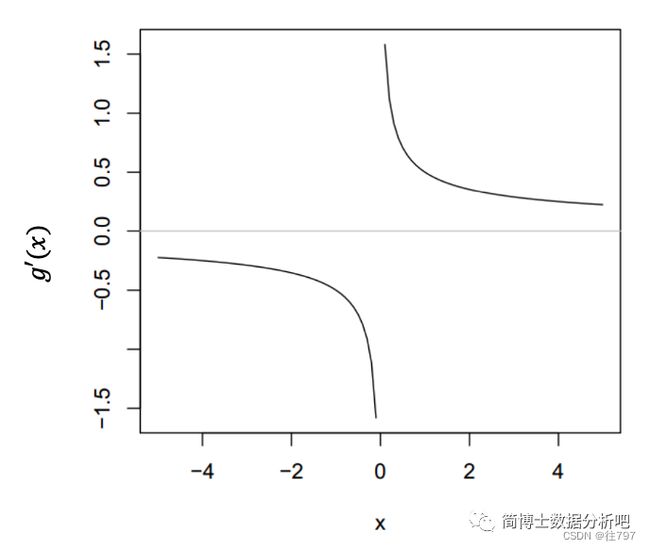
假如我们用牛顿法，求解下面这个函数的零点。
首先，我们需要求出它的导函数
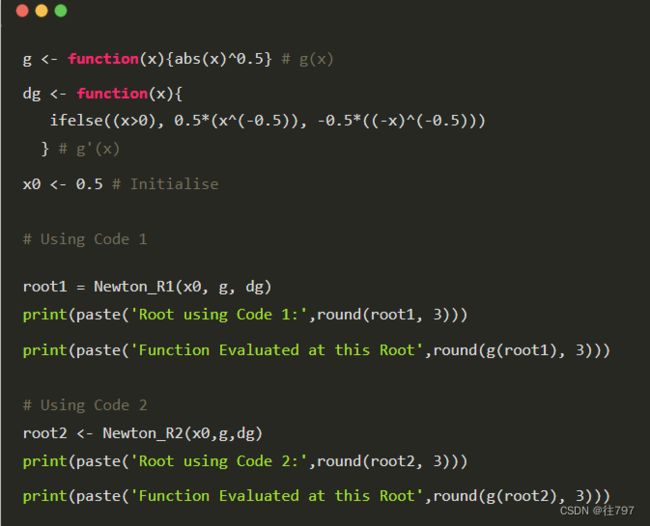
我们发现，这里的导函数是分段函数，现在我们取初始值
，用刚才的两串代码试一下。
案例2：
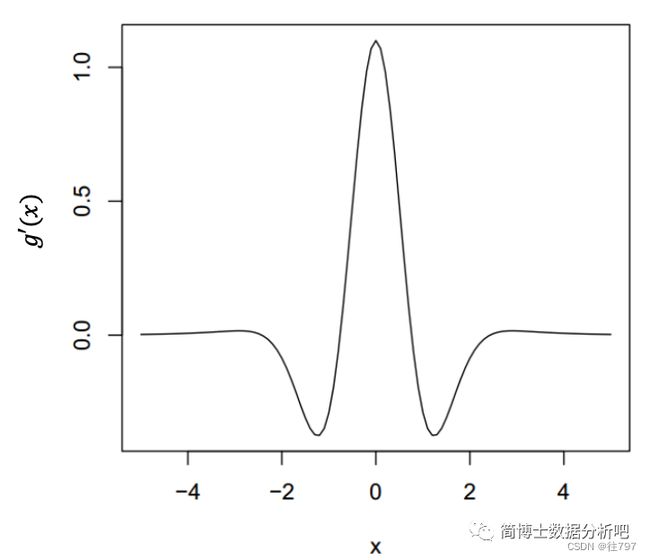
假如我们用牛顿法，求解下面这个函数的「零点」。
导函数如下：
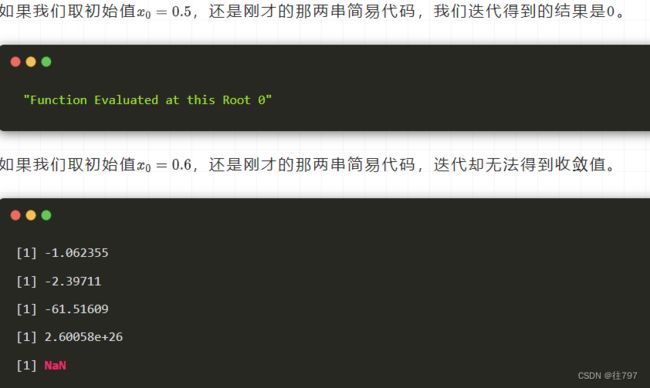
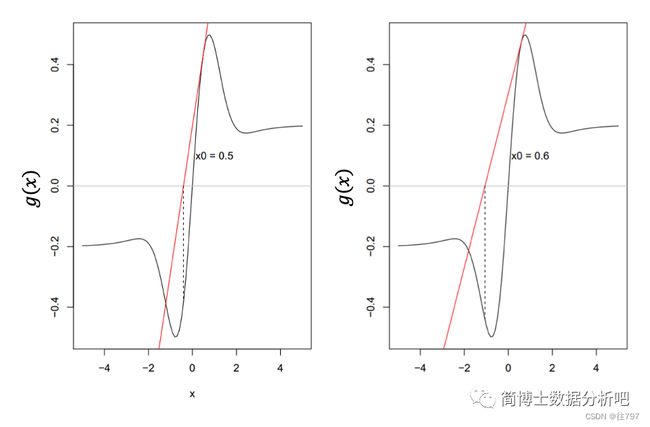
什么原因呢？一起来看图：
因为如果选了0.6做初始值，迭代点就会距离零点越来越远了，跑到天涯海角去啦。
这说明，「牛顿法对初始值非常敏感，不同的初始值是否收敛就存在着不同」！
案例3
假如我们用牛顿法，求解下面这个函数的零点。
其导函数：
两个初始值彼此之间挨得很近，怎么得到的结果却大相径庭呢？
因为两者的收敛过程相差很大。
这说明，「在牛顿法中不同的初始值，收敛值可能不同」！
因此，给大家一个小tip：
2.下篇
2.1极值的含义
「极值点的定义」：
（应该修改为去心邻域？）
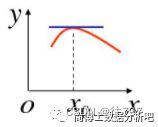
「费马引理」：
所以，如果「函数可微」，想找到「局部极值点」，只要去找导函数为零的位置就可以了。
由此，求解极值的问题就可以转化为寻找导函数零点的问题。
如此一来，也就把我们现在的问题，转化成一个我们曾经已经解决过的问题了，这是数学中常用的一种思想。
即把未知的问题，转变为已知的问题来解决。
2.2如何用牛顿法求 一元极值点
一、怎么寻找极值点
和梯度下降法类似，仍以下山为例，因为只要掌握了「如何求极小值」，求极大值的问题自然也就迎刃而解了，在函数前加一个负号就可以了。
先看个函数：
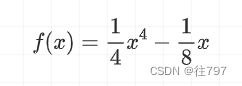
▲f（x）曲线
从图中我们知道f（x）存在极小值，假如现在想求极小值所对应的位置求出来。
怎么求？很简单。求一下它导函数就行。
▲g（x）曲线
于是我们就把问题转化成求解三次多项式根零点的问题啦，这样就回到了「用牛顿法求零点」的方法中。
还记得上篇介绍的迭代公式吗？没错，思路很简单，分成两步走。
二、用牛顿法求极值的算法解读
三、用牛顿法求极值的例题讲解
还是刚才这个例子，采用牛顿法来求解函数的极小值点。
按照算法的步骤，我们分别求出了一阶导函数和二阶导函数。然后就开始代入数值迭代计算吧。
▲极小值求解迭代结果
2.3如何用牛顿法求多元极值点
一、何为多元的概念？
那么如果是要求多元的，也就是涉及到多个参数该怎么办呢？
接下来就要看一下怎么将它推广到一个多元的情况，假如说我们现在有一个函数，这个函数是几元的？
没错，正是 n 元的。那么对他们求一阶导函数，也就意味着是一个梯度向量，对每一个变量求偏导数，依次放在梯度向量里。
如果我们现在的对应是第 i 行，第 j 列该怎么办？
我们求的应该是这样一个二阶导函数，先对 
求偏导，然后再对 
求偏导得出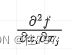 
，每个位置都填上，就得到海森矩阵啦。
二、用牛顿法求多元极值点的算法解读
接着就可以根据向量得出多元的极值求解算法
三、用牛顿法 求多元极小值的例题讲解
计算精度」为
▲计算多元极小值点的迭代数值
