数据结构与算法-Part8——树与二叉树

树结构是数据元素之间具有层次关系的非线性数据结构，树结构可以分为无序树和有序树两种类型，有序树中最常见的是二叉树，其每个结点最多只有两个可分左右的子树。

一丶树的定义与基本术语

Windows，Linux等主流操作系统的文件系统就是一个树型结构的数据结构，根目录是文件树的根结点，子目录是树中的分支节点，文件是树的叶子结点。树结构中，除了根节点没有前驱元素外，每个数据元素都只有一个前驱元素，但可有若干个后继元素。

1：树的定义和表示

树的结点为0时，成为空树，节点数大于0时，为非空树。一个非空树具有以下特点：
1）树T有一个特殊的结点，它没有前驱结点，这个结点为根节点

2）树结点大于1时，根节点之外的其他结点可分为m个互不相交的集合T1,T2,...Tm,其中每个集合具有与树T相同的树结构，成为子树(subtree)。每颗子树的根节点有且仅有一个直接前驱结点，但可以有零或多个直接后继节点。

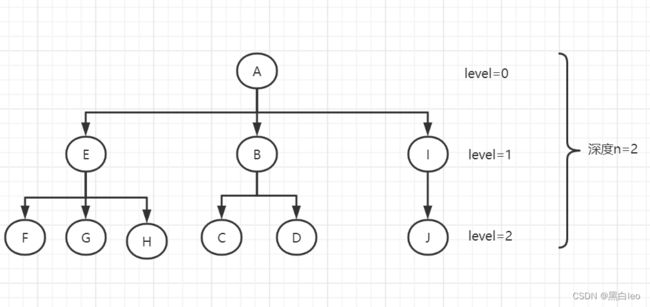
下图显示了一个树，结点树n=10，A为树的根节点，其他结点则分别在A的子树T1,T2,T3，其中T1={B,C,D}，T2={E,F,G,H},T3={I,J}，子树的根分别为B,E,I

 树可以分为有序树和无序树，在无序树中，结点的子树T1,T2,...,Tm之间没有次序关系，如果树中结点的子树T1,T2,...,Tm从左至右都是有次序的，则成为有序树，通常说的树指的是无序树。

若干颗互不相交的树的集合成为森林，给森林加上根结点就变成了一棵树，也可以用广义表表示树，表示形式为A(B(CD)),E(F,G,H),I(J)

2：树的基本术语

1)结点

结点表示树集合中的一个数据元素

2）子节点与父节点

顾名思义，如图中，结点B,E,I是结点A的子树的根，所以A是它们的父节点，它们是A的子节点

3）兄弟节点

同级中的结点，如E,B,I是兄弟节点

4）祖先节点和后代节点

从根结点到结点N所经过的所有结点，称为结点N的祖先节点，例如B和A是C的祖先节点，H,J是结点A的后代节点

5）结点的度和树的度

结点的度是结点所拥有的子树的棵树，而树的度是指树中各节点度的最大值

6）叶子结点和分支结点

度为0的结点定义为叶子结点，没有后继节点，而除叶子以外的其他结点成为分支结点

7）边

连接两个结点为边，如AB,BC

8）路径和路径长度

如A到C的路径为(ABC),路径长度为2

9）结点的层次和树的深度

结点的层次为该结点扩展等级，层次的最大值为树的深度，如A的层次为0，B的层次为1，树的深度为2

3：树的基本操作

1）Initialize:初始化。建立一颗树实例并初始化它的结点集合和边的集合

2）AddNode/AddNodes：在树中设置，添加一个或若干结点

3）Get/Set：访问。获取和设置树中的指定节点

4）Count：求节点数

5）AddEdge：树中添加边

6）Remove：删除数据节点或边

7）Cotains:/IndexOf：查找。在树中查找满足某种条件的结点

8）Traversal：遍历，按某种次序访问树中的所有结点，且每个结点恰好访问一次

9）Copy：复制，复制一棵树

二丶二叉树的定义与实现

有序树中最常见的就是二叉树

1：二叉树的定义

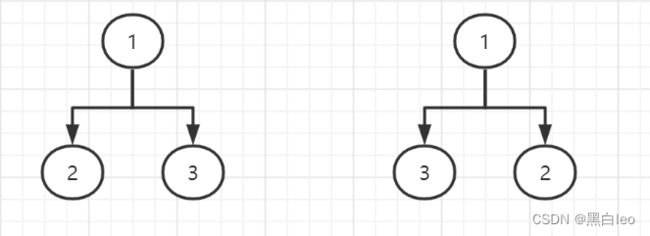
二叉树是一种特殊的树结构，树结构中定义的有关术语，如度，层次等都适用于二叉树，二叉树的结点最多拥有两颗子树，所以二叉树的度最大为2。但是度为2的二叉树与度为2的树在结构上是不等价的，因为二叉树中每个结点的两颗子树有左右之分，而普通的树结构指的是无序树，例如下图

 如果它们看成是二叉树，则是不同的两颗二叉树，如果看成是树，则表示两颗相同的树

因此二叉树有五种基本形态

1）空二叉树

2）只有一个结点（根节点）的二叉树

3）表示由根节点以及非空的左子树和空右子树构成的二叉树

4）表示由根节点以及非空的右子树和空左子树构成的二叉树

5）表示由根节点以及非空的右子树和非空左子树构成的二叉树

例：画出三个结点的树与二叉树

2：二叉树的性质

1）二叉树第i层的结点数目最多为，每层的结点新增2个，指数爆炸

2）在深度为k的二叉树中，则二叉树最多有个结点（K≥0）

当k=0，层次为0，则节点数为1，当k=1,层次为1，节点数为3，当深度k为n，层次为n,则二叉树的总节点数最大为

3)二叉树中，若叶子节点数为n0,2度结点的数目为n2,则n0=n2+1,即，二叉树中叶子结点比度为2的节点数多1

4）如果一颗完全二叉树有n个结点，则其深度

5)满二叉树与完全二叉树的关系

①满二叉树一定是完全二叉树，而完全二叉树不一定是满二叉树，它具有满二叉树的结构而不一定满二叉树，完全二叉树最下面一层可以不满，其上层可以看成是满二叉树

②完全二叉树最下面一层的结点都几种在该层最左边的若干位置

③完全二叉树至多只有最下面最下面两层的度可以小于2

6）若将一颗具有n个结点的完全二叉树的所有节点自下而上，自左至右的顺序编号，结点编号i的取值范围为(0≤i≤n-1)

3：二叉树的存储结构

在计算机中表示二叉树数据结构，可以用顺序存储结构和链式存储结构两种方式，二叉树具有层次关系，因此采用链式存储结构会更灵活，而顺序存储结构适用于完全二叉树

1）二叉树的顺序存储结构

完全二叉树可以用顺序存储结构实现，即将完全二叉树的所有结点按顺序存放在一个数组中，将完全二叉树的结点进行顺序编号，并将编号为i的结点存放在数组中下标为i的单元中，根据性质五可以直接计算得到父节点，左子节点和右子节点的位置

2）二叉树的链式存储结构

为了以链式存储结构实现二叉树，在逻辑上，二叉树结点应有以下3个域：

①数据域data，表示结点的数据元素自身的内容

②左链域left,指向该结点的左子节点

③右链域right，指向该结点的右子结点

二叉树的表示则需记录其根节点root,若二叉树为空，则root置为null,二叉树中某节点的左子节点也代表该节点的左子二叉树，若结点的左子树为空，则左链域left置为空值，即left=null

4：二叉树类的定义

1：二叉树的结点类

为实现二叉树的链式存储结构，将二叉树的结点声明为BinaryTreeNode泛型类，其中有三个成员变量，数据域，链域left和right分别指向左节点和右结点，三个成员变量都定义为私有的，不能被外界访问，通过在类定义中添加相应的共有属性Data，Left和Right让外界访问这些域成员，在创建一个结点时将数据域data初始化为缺省，链域left和right置为null

public class BinaryTreeNode
{
    private T data;  //数据元素
    private BinaryTreeNode left,right; //指向左，右结点的链
    public BinaryTreeNode()
    {
        left=right=null;//left和right为空，data未设置，缺省状态
    }
    //构造有值结点
    public BinaryTreeNode(T d)
    {
        data=d;
        left=right=null;
    }
    public T Data
    {
        get{return data;}
        set{data=value;}
    }
    public BinaryTreeNodeLeft
    {
        get{return left;}
        set{left=value;}
    }
    public BinaryTreeNodeRight
    {
        get{return Right;}
        set{Right=value;}
    }
}

2：二叉树类

链式存储结构的二叉树用下面定义的BinaryTree类表示，它的成员变量root指向二叉树的根节点

public class BinaryTreeNode
{
    protected BinaryTreeNode root;//指向二叉树的根节点
    public BinaryTreeNodeRoot
    {
        get{return root;}
        set{root=value;}
    }
    public BinaryTree()
    {
        root=null;//构造空二叉树
    }
}

三丶二叉树的遍历

1：二叉树遍历的过程

二叉树的遍历操作就是按照一定规则和次序访问二叉树中的所有结点，并且每个结点仅被访问一次

如果规定对子树的访问按照“先左后右”的次序进行，则遍历二叉树有三种次序：
1）先根次序：访问根结点，遍历左子树，遍历右子树

2）中根次序：遍历左子树，访问根结点，遍历右子树

3）后根次序：遍历左子树，遍历右子树，访问根结点

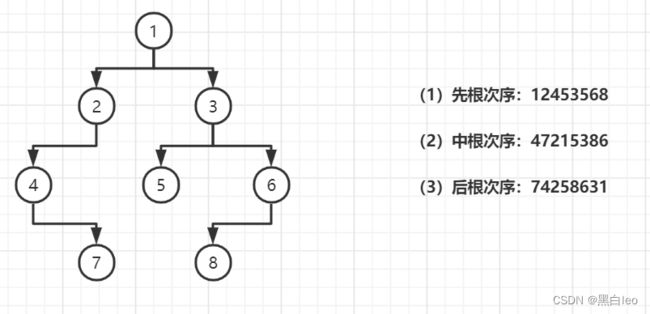
以下图为例演示三种遍历顺序：

先根次序或后跟次序遍历序列能反映双亲与孩子结点的层次关系，中根次序遍历序列能反映兄弟结点间的左右次序 

2：二叉树遍历的递归算法

1）：按先根次序遍历二叉树的递归算法

若二叉树为空，则该操作为空操作，直接返回，否则从根结点开始

①访问当前结点

②按先根次序遍历当前结点的左子树

③按先根次序遍历当前结点的右子树

ShowPreOrder方法在控制台显示按先根次序遍历二叉树得到的结点序列的值

public void ShowPreOrder()
{
    Console.WriteLine(this.Data+" ");
    BinaryTreeNode q=this.Left;
    if(q!=null)
    {
        q.ShowPreOrder();
    }
    q=this.Right;
    if(q!=null)
    {
        q.ShowPreOrder();
    }
}

TraveralPreOrder方法更为一般化，它将各个结点的值按照先根次序放在一个线性表中

public void TraversalPreOrder(IListsql)
{
    sql.Add(this.data);
    BinaryTreeNodeq=this.Left;
    if(q!=null)
    {
        q.TraversalPreOrder(sql);
        q=this.Right;
        if(q!=null)
        {
            q.TraversalPreOrder(sql);
        }
    }
}

2）：按中根次序遍历二叉树的递归算法

①按中根次序遍历当前结点的左子树；

②访问当前结点；

③按中根次序遍历当前结点的右子树；

在二叉树结点类BinaryTreeNode中，ShowInOrder方法和TraveralPreOrder方法同上

public void ShowInOrder()
{
    BinaryTreeNode q=this.Left;
    if(q!=null)
    {
        q.ShowInOrder();
    }
    q=this.Right;
    if(q!=null)
    {
        q.ShowInOrder();
    }
}

public void TraversalInOrder(IListsql)
{
    BinaryTreeNodeq=this.Left;
    if(q!=null)
    {
        q.TraversalInOrder(sql);
    sql.Add(this.Data);
    q=this.Right;
    if(q!=null)
    {
        q.TraversalInOrder(sql);
    }
}

3）：按后根次序遍历二叉树的递归算法

①按后根次序遍历当前结点的左子树

②按后根次序遍历当前结点的右子树

③访问当前结点

同样有ShowPostOrder和TraversalPostOrder方法来遍历

public void ShowPostOrder()
{
    BinaryTreeNode q=this.Left;
    if(q!=null)
    {
        q.ShowPostOrder();
    }
    q=this.Right;
    if(q!=null)
    {
        q.ShowPostOrder();
    }
    Console.Write(this.Data+" ");
}

public void TraversalPostOrder(IListsql)
{
    BinaryTreeNodeq=this.Left;
    if(q!=null)
    {
        q.TraversalPostOrder(sql);
    sql.Add(this.Data);
    q=this.Right;
    if(q!=null)
    {
        q.TraversalPostOrder(sql);
    }
    sql.Add(this.Data);
}

3：二叉树遍历的非递归算法

4：按层次遍历二叉树

四丶构建二叉树

1：建立链式存储结构的完全二叉树

2：根据广义表表示建立二叉树

3：根据先根和中根次序遍历序列建立二叉树

五丶线索二叉树

1：线索与线索二叉树

2：线索二叉树类的实现

3：二叉树的中序线索化

4：线索二叉树的遍历

六丶用二叉树表示树与森林