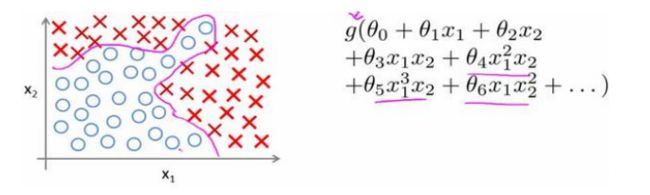机器学习笔记 -- 神经网络
1、什么是神经网络
1.1 非线性假设
无论是线性回归还是逻辑回归,都存在这样一个缺陷,那就是当特征过多时,计算量会非常大。这时,神经网络应运而生,极大地弥补了这方面的缺点。
1.2 神经元与大脑
每个神经元都可以看做一个处理单元,它有多个树突(输入),一个轴突(输出)。多个信息经过树突传递到神经元,处理后,再通过轴突输出。这便是神经网络的生物模型。
基于此,我们设计出了类似的神经网络模型。
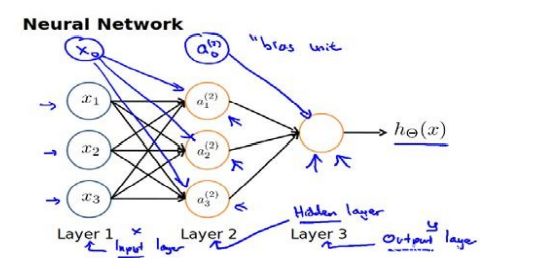
x 1 x_1 x1、 x 2 x_2 x2、 x 3 x_3 x3为输入层; a 1 ( 2 ) a_1^{(2)} a1(2)、 a 2 ( 2 ) a_2^{(2)} a2(2)、 a 3 ( 2 ) a_3^{(2)} a3(2)为中间层,也即隐藏层; a ( 3 ) a^{(3)} a(3)为输出层。每一层的输出变量都是下一层的输入变量。
计算时,我们需要为每一层加上偏差单位
对于上图所示的模型,激活单元和输出分别表达为:
a 1 ( 2 ) = g ( Θ 10 ( 1 ) x 0 + Θ 11 ( 1 ) x 1 + Θ 12 ( 1 ) x 2 + Θ 13 ( 1 ) x 3 ) a 2 ( 2 ) = g ( Θ 20 ( 1 ) x 0 + Θ 21 ( 1 ) x 1 + Θ 22 ( 1 ) x 2 + Θ 23 ( 1 ) x 3 ) a 3 ( 2 ) = g ( Θ 30 ( 1 ) x 0 + Θ 31 ( 1 ) x 1 + Θ 32 ( 1 ) x 2 + Θ 33 ( 1 ) x 3 ) h θ ( x ) = g ( Θ 10 ( 2 ) a 0 ( 2 ) + Θ 11 ( 2 ) a 1 ( 2 ) + Θ 12 ( 2 ) a 2 ( 2 ) + Θ 13 ( 2 ) a 3 ( 2 ) ) \begin{aligned} &a_{1}^{(2)}=g\left(\Theta_{10}^{(1)} x_{0}+\Theta_{11}^{(1)} x_{1}+\Theta_{12}^{(1)} x_{2}+\Theta_{13}^{(1)} x_{3}\right) \\ &a_{2}^{(2)}=g\left(\Theta_{20}^{(1)} x_{0}+\Theta_{21}^{(1)} x_{1}+\Theta_{22}^{(1)} x_{2}+\Theta_{23}^{(1)} x_{3}\right) \\ &a_{3}^{(2)}=g\left(\Theta_{30}^{(1)} x_{0}+\Theta_{31}^{(1)} x_{1}+\Theta_{32}^{(1)} x_{2}+\Theta_{33}^{(1)} x_{3}\right) \\ &h_{\theta}(x)=g\left(\Theta_{10}^{(2)} a_{0}^{(2)}+\Theta_{11}^{(2)} a_{1}^{(2)}+\Theta_{12}^{(2)} a_{2}^{(2)}+\Theta_{13}^{(2)} a_{3}^{(2)}\right) \end{aligned} a1(2)=g(Θ10(1)x0+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3)a2(2)=g(Θ20(1)x0+Θ21(1)x1+Θ22(1)x2+Θ23(1)x3)a3(2)=g(Θ30(1)x0+Θ31(1)x1+Θ32(1)x2+Θ33(1)x3)hθ(x)=g(Θ10(2)a0(2)+Θ11(2)a1(2)+Θ12(2)a2(2)+Θ13(2)a3(2))
注意 θ \theta θ 的下标表示。
1.3 多元分类
不同于二元分类,仅0和1就可以表示,多元分类用向量形式表达不同分类。
[ 1 0 0 0 ] , [ 0 1 0 0 ] , [ 0 0 1 0 ] , [ 0 0 0 1 ] \left[\begin{array}{l} 1 \\ 0 \\ 0 \\ 0 \end{array}\right],\left[\begin{array}{l} 0 \\ 1 \\ 0 \\ 0 \end{array}\right],\left[\begin{array}{l} 0 \\ 0 \\ 1 \\ 0 \end{array}\right],\left[\begin{array}{l} 0 \\ 0 \\ 0 \\ 1 \end{array}\right] ⎣⎢⎢⎡1000⎦⎥⎥⎤,⎣⎢⎢⎡0100⎦⎥⎥⎤,⎣⎢⎢⎡0010⎦⎥⎥⎤,⎣⎢⎢⎡0001⎦⎥⎥⎤
以上分别表示四分类中的第1、2、3、4类。
2、神经网络的计算
2.1 代价函数
逻辑回归中,
J ( θ ) = − 1 m [ ∑ j = 1 n y ( i ) log h θ ( x ( i ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J(\theta)=-\frac{1}{m}\left[\sum_{j=1}^{n} y^{(i)} \log h_{\theta}\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right]+\frac{\lambda}{2 m} \sum_{j=1}^{n} \theta_{j}^{2} J(θ)=−m1[j=1∑ny(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]+2mλj=1∑nθj2
类似的,神经网络中
J ( Θ ) = − 1 m [ ∑ i = 1 m ∑ k = 1 k y k ( i ) log ( h Θ ( x ( i ) ) ) k + ( 1 − y k ( i ) ) log ( 1 − ( h Θ ( x ( i ) ) ) k ) ] + λ 2 m ∑ l = 1 L − 1 ∑ i = 1 s l ∑ j = 1 s s + 1 ( Θ j i ( l ) ) 2 \begin{aligned} &J(\Theta)=-\frac{1}{m}\left[\sum_{i=1}^{m} \sum_{k=1}^{k} y_{k}^{(i)} \log \left(h_{\Theta}\left(x^{(i)}\right)\right)_{k}+\left(1-y_{k}^{(i)}\right) \log \left(1-\left(h_{\Theta}\left(x^{(i)}\right)\right)_{k}\right)\right] \\ &+\frac{\lambda}{2 m} \sum_{l=1}^{L-1} \sum_{i=1}^{s_{l}} \sum_{j=1}^{s_{s}+1}\left(\Theta_{j i}^{(l)}\right)^{2} \end{aligned} J(Θ)=−m1[i=1∑mk=1∑kyk(i)log(hΘ(x(i)))k+(1−yk(i))log(1−(hΘ(x(i)))k)]+2mλl=1∑L−1i=1∑slj=1∑ss+1(Θji(l))2
不同的是,对于每一行特征,我们都会给出 K 个预测,然后将它们的代价函数进行加和。
计算时,将 K 个预测值中概率最大的值作为最终的预测。
2.2 反向传播
2.2.1 正向传递
假设一个三层网络
传递过程:
a ( 1 ) = x z ( 2 ) = θ ( 1 ) a ( 1 ) a ( 2 ) = g ( z ( 2 ) ) ( a d d a 0 ( 2 ) ) z ( 3 ) = θ ( 2 ) a ( 2 ) h = a ( 3 ) = g ( z ( 3 ) ) \begin{aligned} &a^{(1)}=x \\ &z^{(2)}=\theta^{(1)} a^{(1)} \\ &a^{(2)}=g\left(z^{(2)}\right)\left(add a_{0}^{(2)}\right) \\ &z^{(3)}=\theta^{(2)} a^{(2)} \\ &h=a^{(3)}=g\left(z^{(3)}\right) \end{aligned} a(1)=xz(2)=θ(1)a(1)a(2)=g(z(2))(adda0(2))z(3)=θ(2)a(2)h=a(3)=g(z(3))
2.2.2 反向传播
首先定义误差 δ l \delta^{l} δl:
δ ( l ) = ∂ J ∂ z ( l ) \delta^{(l)}=\frac{\partial J}{\partial z^{(l)}} δ(l)=∂z(l)∂J
需要注意的是,这里的误差表示每个输入对于最终偏差的“贡献”。
根据链式求导法则,得到四个基本公式,具体推导 参考
δ i ( L ) = − ( y i − a i ( L ) ) f ′ ( z i ( L ) ) δ i ( l ) = ( ∑ j = 1 n l + 1 δ j ( l + 1 ) w j i ( l + 1 ) ) f ′ ( z i ( l ) ) ∂ E ∂ w i j ( l ) = δ i ( l ) a j ( l − 1 ) ∂ E ∂ b i ( l ) = δ i ( l ) \begin{aligned} &\delta_{i}^{(L)}=-\left(y_{i}-a_{i}^{(L)}\right) f^{\prime}\left(z_{i}^{(L)}\right) \\ &\delta_{i}^{(l)}=\left(\sum_{j=1}^{n_{l+1}} \delta_{j}^{(l+1)} w_{j i}^{(l+1)}\right) f^{\prime}\left(z_{i}^{(l)}\right) \\ &\frac{\partial E}{\partial w_{i j}^{(l)}}=\delta_{i}^{(l)} a_{j}^{(l-1)} \\ &\frac{\partial E}{\partial b_{i}^{(l)}}=\delta_{i}^{(l)} \end{aligned} δi(L)=−(yi−ai(L))f′(zi(L))δi(l)=(j=1∑nl+1δj(l+1)wji(l+1))f′(zi(l))∂wij(l)∂E=δi(l)aj(l−1)∂bi(l)∂E=δi(l)
得到向量形式
δ ( L ) = − ( y − a ( L ) ) ⊙ f ′ ( z ( L ) ) δ ( l ) = ( ( W ( l + 1 ) ) ⊤ δ ( l + 1 ) ) ⊙ f ′ ( z ( l ) ) ∂ E ∂ W ( l ) = δ ( l ) ( a ( l − 1 ) ) ⊤ ∂ E ∂ b ( l ) = δ l \begin{aligned} &\boldsymbol{\delta}^{(L)}=-\left(\boldsymbol{y}-\boldsymbol{a}^{(L)}\right) \odot f^{\prime}\left(\boldsymbol{z}^{(L)}\right) \\ &\boldsymbol{\delta}^{(l)}=\left(\left(W^{(l+1)}\right)^{\top} \boldsymbol{\delta}^{(l+1)}\right) \odot f^{\prime}\left(\boldsymbol{z}^{(l)}\right) \\ &\frac{\partial E}{\partial W^{(l)}}=\boldsymbol{\delta}^{(l)}\left(\boldsymbol{a}^{(l-1)}\right)^{\top} \\ &\frac{\partial E}{\partial b^{(l)}}=\boldsymbol{\delta}^{l} \end{aligned} δ(L)=−(y−a(L))⊙f′(z(L))δ(l)=((W(l+1))⊤δ(l+1))⊙f′(z(l))∂W(l)∂E=δ(l)(a(l−1))⊤∂b(l)∂E=δl
结合上述三层网络,有
δ ( 3 ) = h − y δ ( 2 ) = ( θ ( 2 ) ) T δ ( 3 ) g ′ ( z ( 2 ) ) \delta^{(3)}=h-y \\ \delta^{(2)}=\left(\theta^{(2)}\right)^{T} \delta^{(3)} g^{\prime}\left(z^{(2)}\right) δ(3)=h−yδ(2)=(θ(2))Tδ(3)g′(z(2))
输入层没有误差。
根据式(BP-3)得到梯度,用 Δ ( l ) \Delta^{(l)} Δ(l)表示
Δ ( 2 ) = a ( 2 ) δ ( 3 ) Δ ( 1 ) = a ( 1 ) δ ( 2 ) \Delta^{(2)}=a^{(2)} \delta^{(3)}\\ \Delta^{(1)}=a^{(1)} \delta^{(2)} Δ(2)=a(2)δ(3)Δ(1)=a(1)δ(2)
最后得到总梯度向量
D = 1 m ( Δ ( 1 ) + Δ ( 2 ) ) D=\frac{1}{m}\left(\Delta^{(1)}+\Delta^{(2)}\right) D=m1(Δ(1)+Δ(2))
2.2.3 注意要点
1、链式求导,注意上下标;
2、注意向量点乘和叉乘;
3、计算时注意向量维度
4、sigmoid函数求导
g ′ ( z ) = d d z g ( z ) = g ( z ) ( 1 − g ( z ) ) g^{\prime}(z)=\frac{d}{d z} g(z)=g(z)(1-g(z)) g′(z)=dzdg(z)=g(z)(1−g(z))
5、输出层误差的形式:参考
常见的损失函数有两种:均方差损失函数 和 交叉熵损失函数
(1)均方差损失函数
E = 1 2 ∥ y − a ∥ 2 = 1 2 ( y − a ) 2 E=\frac{1}{2}\left\|\boldsymbol{y}-\boldsymbol{a}\right\|^2=\frac{1}{2}(\boldsymbol{y}-\boldsymbol{a})^2 E=21∥y−a∥2=21(y−a)2
则,输出层误差
δ ( L ) = ∂ E ∂ z ( L ) = ∂ E ∂ a ( L ) ∂ a ( L ) ∂ z ( L ) = − ( y − a ( L ) ) ⊙ f ′ ( z ( L ) ) \boldsymbol{\delta}^{(L)}=\frac{\partial E}{\partial z^{(L)}}=\frac{\partial E}{\partial a^{(L)}}\frac{\partial a^{(L)}}{\partial z^{(L)}}=-\left(\boldsymbol{y}-\boldsymbol{a}^{(L)}\right) \odot f^{\prime}\left(\boldsymbol{z}^{(L)}\right) δ(L)=∂z(L)∂E=∂a(L)∂E∂z(L)∂a(L)=−(y−a(L))⊙f′(z(L))
(2)交叉熵损失函数
C = − y l o g a − ( 1 − y ) l o g ( 1 − a ) C=- \boldsymbol{y}log\boldsymbol{a}-(1-\boldsymbol{y})log(1-\boldsymbol{a}) C=−yloga−(1−y)log(1−a)
则,输出层误差
δ ( L ) = ∂ E ∂ z ( L ) = ∂ E ∂ a ( L ) ∂ a ( L ) ∂ z ( L ) = a ( L ) − y \boldsymbol{\delta}^{(L)}=\frac{\partial E}{\partial z^{(L)}}=\frac{\partial E}{\partial a^{(L)}}\frac{\partial a^{(L)}}{\partial z^{(L)}}=\boldsymbol{a}^{(L)}-\boldsymbol{y} δ(L)=∂z(L)∂E=∂a(L)∂E∂z(L)∂a(L)=a(L)−y
采用交叉熵函数,形式较为简单,且性能较好。
6、误差递推公式推导
δ i ( l ) ≡ ∂ E ∂ z i ( l ) = ∑ j = 1 n l + 1 ∂ E ∂ z j ( l + 1 ) ∂ z j ( l + 1 ) ∂ z i ( l ) = ∑ j = 1 n l + 1 δ j ( l + 1 ) ∂ z j ( l + 1 ) ∂ z i ( l ) = ∑ j = 1 n l + 1 δ j ( l + 1 ) ∂ z j ( l + 1 ) ∂ a i ( l ) ∂ a i ( l ) ∂ z i ( l ) = ∑ j = 1 n l + 1 δ j ( l + 1 ) w j i ( l + 1 ) f ′ ( z i ( l ) ) = ( ∑ j = 1 n l + 1 δ j ( l + 1 ) w j i ( l + 1 ) ) f ′ ( z i ( l ) ) \begin{aligned} \delta_{i}^{(l)} & \equiv \frac{\partial E}{\partial z_{i}^{(l)}} \\ &=\sum_{j=1}^{n_{l+1}} \frac{\partial E}{\partial z_{j}^{(l+1)}} \frac{\partial z_{j}^{(l+1)}}{\partial z_{i}^{(l)}} \\ &=\sum_{j=1}^{n_{l+1}} \delta_{j}^{(l+1)} \frac{\partial z_{j}^{(l+1)}}{\partial z_{i}^{(l)}}\\ &=\sum_{j=1}^{n_{l+1}} \delta_{j}^{(l+1)} \frac{\partial z_{j}^{(l+1)}}{\partial a_{i}^{(l)}} \frac{\partial a_{i}^{(l)}}{\partial z_{i}^{(l)}}\\ &=\sum_{j=1}^{n_{l+1}} \delta_{j}^{(l+1)} w_{j i}^{(l+1)} f^{\prime}\left(z_{i}^{(l)}\right)\\ &=\left(\sum_{j=1}^{n_{l+1}} \delta_{j}^{(l+1)} w_{j i}^{(l+1)}\right) f^{\prime}\left(z_{i}^{(l)}\right) \end{aligned} δi(l)≡∂zi(l)∂E=j=1∑nl+1∂zj(l+1)∂E∂zi(l)∂zj(l+1)=j=1∑nl+1δj(l+1)∂zi(l)∂zj(l+1)=j=1∑nl+1δj(l+1)∂ai(l)∂zj(l+1)∂zi(l)∂ai(l)=j=1∑nl+1δj(l+1)wji(l+1)f′(zi(l))=(j=1∑nl+1δj(l+1)wji(l+1))f′(zi(l))
表达为向量形式,即
δ ( l ) = ( ( W ( l + 1 ) ) ⊤ δ ( l + 1 ) ) ⊙ f ′ ( z ( l ) ) \boldsymbol{\delta}^{(l)}=\left(\left(W^{(l+1)}\right)^{\top} \boldsymbol{\delta}^{(l+1)}\right) \odot f^{\prime}\left(\boldsymbol{z}^{(l)}\right) δ(l)=((W(l+1))⊤δ(l+1))⊙f′(z(l))
欢迎关注公众号哦~~
![]()
3、课后习题
3.1 多类别逻辑回归
# @Time : 2021/10/13 19:41
# @Author : xiao cong
# @Function :多类别逻辑回归、神经网络
import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat # 用于导入mat文件
data = loadmat("ex3data1.mat") # 包含5000个20*20像素的手写字体图像,以及他对应的数字。另外,数字0的y值,对应的是10
# print(type(data)) # data为dict类型
X = data["X"]
y = data["y"]
print(X.shape,y.shape)
# ***********************************************************************************************
# 数据可视化(随机展示100个数据)
image_idx = np.random.choice(np.array(X.shape[0]),100) # 随机生成100个索引,返回一维数组
images = X[image_idx,:]
def displayData(img):
fig, ax = plt.subplots(10, 10, sharex=True, sharey=True,figsize=(10, 10)) # ax表示子图;sharex=True表示共享x轴
for row in range(10):
for column in range(10):
ax[row,column].imshow(img[10*row+column].reshape(20,20).T,cmap='gray')
plt.xticks([]) # 去掉坐标轴,比较美观
plt.yticks([])
plt.show()
#displayData(images)
# ********************************************************************************
# 计算代价函数和梯度下降函数
# sigmod 函数
def sigmod(z):
return 1/(1+np.exp(-z))
# 正则化代价函数
def costReg(theta,X,y,Lambda): # 此处theta为一维数组(n,),而非(n,1),二者有区别
m = X.shape[0]
h = sigmod(np.dot(X,theta))
first = -np.dot(y.T,np.log(h))
second = np.dot((1-y).T,np.log(1-h))
Reg = Lambda/(2*m)*(np.dot(theta.T,theta)-theta[0]**2) # 不惩罚theta_0
return (first-second)/m + Reg
# 正则化梯度下降向量
# 此处区别于梯度下降函数,这里用优化函数进行优化,形式会有所不同
def gradientReg(theta,X,y,Lambda):
m = X.shape[0]
Error = sigmod(np.dot(X, theta)) - y
first = np.dot(X.T,Error)/m
Reg = (Lambda/m)*theta[1:]
Reg = np.insert(Reg,0,values=0,axis=0)
return first + Reg
# *****************************************************************************
# 一对多分类
from scipy.optimize import minimize
X = np.insert(X,0,values=1,axis=1)
y = y.flatten() # 降维成一维向量,与theta匹配,便于带进函数进行计算
def one_vs_all(X,y,Lambda,K):
n = X.shape[1]
theta_all = np.zeros((K,n))
for i in range(1,K+1):
theta_i = np.zeros(n,) # 此处是一个一维数组
res = minimize(fun=costReg,x0=theta_i,args=(X,y==i,Lambda),method='TNC',jac=gradientReg)
theta_all[i-1,:] = res.x
return theta_all
Lambda = 1
K = 10
theta_final = one_vs_all(X,y,Lambda,K)
print(theta_final) # 10行401列
# ****************************************************
# 预测
def Predict(X,theta_final):
h = sigmod(np.dot(X,theta_final.T)) # h为预测值,5000行10列,即对每个标签都进行了预测
h_argmax = np.argmax(h,axis=1) # 找出每行概率最大的标签值,作为预测值,即axis=1方向.返回最大值的索引值
return h_argmax + 1 # 此处注意:如某行概率最大值索引值为0,则预测值为1,以此类推
predict_y = Predict(X,theta_final)
accuracy = np.mean(predict_y == y)
print("预测准确率为{:.2%}".format(accuracy))
3.2 前馈神经网络预测
# @Time : 2021/10/16 20:56
# @Author : xiao cong
# @Function : 前馈神经网络进行预测,权重已经给出
import numpy as np
import scipy.io as sio
data = sio.loadmat("ex3data1.mat") # 包含5000个20*20像素的手写字体图像,以及他对应的数字。另外,数字0的y值,对应的是10
X = data["X"] # data为dict类型
y = data["y"]
X = np.insert(X,0,values=1,axis=1) # 添加一列偏置
y = y.flatten() # 降为一维数组,便于后续计算
theta = sio.loadmat("ex3weights.mat") # 导入权重
# print(theta) # 两层神经网络,两组theta
theta1 = theta['Theta1'] # 输入层到隐藏层的权重
theta2 = theta['Theta2'] # 隐藏层到输出层的权重
print(theta1.shape,theta2.shape)
# 输出(25, 401) (10, 26),隐藏层有25和神经元(不包括偏置)
3.3 反向传播算法
# @Time : 2021/10/18 11:01
# @Author : xiao cong
# @Function : 反向传播神经网络
import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat # 用于导入mat文件
# 导入数据集
data = loadmat("ex4data1.mat") # 包含5000个20*20像素的手写字体图像,以及他对应的数字。另外,数字0的y值,对应的是10
# print(type(data)) # data为dict类型
X = data["X"]
y0 = data["y"]
print("X.shape={}, y0.shape={}".format(X.shape, y0.shape))
# 对y进行独热编码处理(将0-9对应为只含有0和1的数列)
def one_hot_encoder(y):
res = [] # 承接转换后的数组
for i in y: # i的范围为1-10
y_temp = np.zeros(10)
y_temp[i - 1] = 1
res.append(y_temp)
return np.array(res)
y = one_hot_encoder(y0)
# 导入权重
theta = loadmat("ex4weights.mat") # 导入权重
theta1 = theta['Theta1'] # 输入层到隐藏层的权重
theta2 = theta['Theta2'] # 隐藏层到输出层的权重
print("theta1.shape={}, theta2.shape={}".format(theta1.shape, theta2.shape))
# 序列化权重参数 (这里是为后面调用优化函数做准备,需要将theta转化为一维数组)
def serialize(a, b):
return np.append(a.flatten(), b.flatten())
theta_serialize = serialize(theta1, theta2)
# 解序列化 (这里是为了后面计算代价函数等,需要还原成原来的函数)
def deserialize(theta_serialize):
theta1 = theta_serialize[:25 * 401].reshape(25, 401)
theta2 = theta_serialize[25 * 401:].reshape(10, 26)
return theta1, theta2
# ***********************************************************************************************
'''数据可视化(随机展示100个数据)'''
image_idx = np.random.choice(np.array(X.shape[0]), 100) # 随机生成100个索引,返回一维数组
images = X[image_idx, :]
def displayData(img):
fig, ax = plt.subplots(10, 10, sharex=True, sharey=True, figsize=(10, 10)) # ax表示子图;sharex=True表示共享x轴
for row in range(10):
for column in range(10):
ax[row, column].imshow(img[10 * row + column].reshape(20, 20).T, cmap='gray')
plt.xticks([]) # 去掉坐标轴,比较美观
plt.yticks([])
plt.show()
displayData(images)
# ***********************************************************************************************
'''前向传播和代价函数'''
# 定义sigmod函数
def sigmoid(z):
return 1 / (1 + np.exp(-z))
# 定义前向传播函数
def feed_forward(theta_serialize, X):
theta1, theta2 = deserialize(theta_serialize)
a1 = np.insert(X, 0, values=1, axis=1) # a1维度:(5000,401)
z2 = np.dot(a1, theta1.T) # z2维度:(5000,25)
a2 = sigmoid(z2)
a2 = np.insert(a2, 0, values=1, axis=1) # a2维度:(5000,26)
z3 = np.dot(a2, theta2.T) # z3维度:(5000,10)
h = sigmoid(z3)
return a1, z2, a2, z3, h
# 定义代价函数
def cost(theta_serialize, X, y):
a1, z2, a2, z3, h = feed_forward(theta_serialize, X)
m = X.shape[0]
J = -(1/m) * np.sum(y*np.log(h) + (1-y)*np.log(1-h)) # 这里用*,即对应元素相乘,非矩阵相乘
return J
print("J=", cost(theta_serialize, X, y))
# 正则化代价函数
def costReg(theta_serialize, X, y, Lambda):
a1, z2, a2, z3, h = feed_forward(theta_serialize, X)
m = X.shape[0]
first = -(1/m) * np.sum(y*np.log(h+1e-5) + (1-y)*np.log(1-h+1e-5))
Reg = (Lambda/(2*m)) * (np.sum(theta1[:,1:]**2) + np.sum(theta2[:,1:]**2)) # 不对偏置项系数正则化
return first + Reg
print("J_Reg=",costReg(theta_serialize, X, y, Lambda=1))
# *********************************************************************************
'''反向传播'''
# 定义梯度向量
def sigmoid_gradient(z):
return sigmoid(z) * sigmoid(1-z) # 注意是点乘
def gradient(theta_serialize, X, y):
m = X.shape[0]
theta1, theta2 = deserialize(theta_serialize)
a1, z2, a2, z3, h = feed_forward(theta_serialize, X)
delta3 = h - y
delta2 = np.dot(delta3, theta2[:,1:])*sigmoid_gradient(z2) # 不包括theta0
Delta2 = np.dot(delta3.T, a2) / m # theta2的梯度
Delta1 = np.dot(delta2.T, a1) / m # theta1的梯度
return serialize(Delta1, Delta2)
# 梯度检验(比较两种方法计算得到的梯度是否近似)
def gradient_checking(theta_serialize, X, y, e=1e-4):
gradapprox = np.zeros(theta_serialize.shape) # 记录计算得到的近似梯度
for i in range(len(theta_serialize)):
plus = theta_serialize
plus[i] = plus[i] + e
minus = theta_serialize
minus[i] = minus[i] - e
gradapprox[i] = (costReg(plus, X, y, Lambda=1) - costReg(minus, X, y, Lambda=1))/(2*e)
grad = gradient(theta_serialize, X, y)
diff = np.linalg.norm(gradapprox - grad) / np.linalg.norm(gradapprox + grad) # 范数
# 这里np.linalg.norm 意思是求向量模长
print('If your backpropagation implementation is correct,\nthe relative difference will be'
' smaller than 10e-9 (assume epsilon=0.0001).\nRelative Difference: {}\n'.format(
diff))
# 带正则化项的梯度向量
def gradientReg(theta_serialize, X, y, Lambda = 1):
m = X.shape[0]
Delta1, Delta2 = deserialize(gradient(theta_serialize, X, y))
theta1[:,0] = 0
theta2[:,0] = 0 # 不惩罚偏置项参数
Delta1_reg = Delta1 + (Lambda/m) * theta1
Delta2_reg = Delta2 + (Lambda/m) * theta2
return serialize(Delta1_reg, Delta2_reg)
# ************************************************************************************
'''优化参数'''
# theta 初始化(这里不可以再取0)
def random_init(size):
return np.random.uniform(-0.12, 0.12, size) # 均匀分布
# 优化参数
from scipy.optimize import minimize
from sklearn.metrics import classification_report # 评价报告
def nn_training(X, y):
init_theta = random_init(25*401 + 10*26)
res = minimize(fun=costReg,
x0=init_theta,
args=(X, y, 1),
method='TNC',
jac=gradientReg,
options={'maxiter': 400})
return res
res = nn_training(X, y)
print(res)
# 计算准确率
def accuracy(theta, X, y0):
_, _, _, _, h = feed_forward(theta, X)
y_pred = np.argmax(h, axis=1) + 1 # 0~9 ==> 1~10
print(classification_report(y0, y_pred))
accuracy = np.mean(y_pred == y0.reshape(5000,))
print("预测准确率为{:.2%}".format(accuracy))
accuracy(res.x, X, y0)
# ***********************************************************************************
# 可视化隐藏层
def plot_hidden_layer(theta):
theta1, _, = deserialize(theta)
hidden_layer = theta1[:,1:] # 不包括偏置项 (25*400)
fig, ax = plt.subplots(5, 5, sharex=True, sharey=True, figsize=(10, 10)) # ax表示子图;sharex=True表示共享x轴
for row in range(5):
for column in range(5):
ax[row, column].imshow(hidden_layer[5 * row + column].reshape(20, 20).T, cmap='gray')
plt.xticks([]) # 去掉坐标轴,比较美观
plt.yticks([])
plt.show()
plot_hidden_layer(res.x)