短时傅里叶变换STFT原理
短时傅里叶变换STFT原理
-
- 一.平稳信号与非平稳信号
- 二.关于傅里叶变换(FT)
-
- 1.傅里叶变换定义
- 2.傅里叶变换的缺陷
- case1.
- case2.
- case3:
- case4:
- 三.关于短时傅里叶变换(STFT)理论
-
- 1.STFT定义
- 2.STFT具体步骤及相关概念
-
- 1.STFT具体步骤
- 2.时间分辨率和频率分辨率
-
- 2.1分辨率的影响因素
- 2.2提高频率分辨率的方法
- 四.STFT的MATLAB实现(非调用函数)
-
- 1.算法实现
- 2. 介绍MATLAB中 spectrogram函数 并绘图
-
- 1.Note: spectrogram()函数的句法和参数大概含义(物理意义和取值范围)可参考[MATLAB help center](https://ww2.mathworks.cn/help/signal/ref/spectrogram.html#bultpz_-2)。函数的底层代码可以在MATLAB命令行窗口输入open/eidt spectrogram 查看。
- 2.如何根据绘制图形理解返回参数!
- 3.MTALAB 中的stft函数
- 五.关于python中实现STFT的函数
-
- 1.scipy.signal.stft函数
- 2.matplotlib.specgram函数
- 七.短时傅里叶变换(STFT)的缺点(非调用函数)
- 八.声明
- 参考文献
- 本人初学者,对于STFT的原理和实现都一头雾水,总结学习过程遇到的问题,汇总参考的文档,写博客记录一下,以此促进学习!
一.平稳信号与非平稳信号
在开始之前,我们需要先理清什么是平稳信号,什么是非平稳信号。我们知道,自然界中几乎所有信号都是非平稳信号,比如我们的语音信号就是典型的非平稳信号。那么何谓平稳信号和非平稳信号呢?一个通俗的理解即,平稳信号在不同时间得到的采样值的统计特性(比如期望、方差等)是相同的,非平稳信号则与之相反,其特性会随时间变化。在信号处理中,这个特性通常指频率!!!!。
在通信原理中平稳严格定义如下:
严平稳随机过程:随机过程统计特性与时间起点无关,即时间平移不影响任何统计特性。
广义平稳随机过程:1.均值不随时间发生变化,2.自相关函数只与时间间隔有关。
那么自相关函数怎么理解呢?
自相关函数R(t1,t2):为了衡量随机过程x(t)在任意两个时刻(t1,t2)上获得的随机变量之间的关联程度。
![]()
由维纳辛钦定理:平稳过程的功率谱密度与其自相关函数是一对傅里叶变换!可以得到信号在不同频率上的能量分布情况,从而估计信号的频谱特性。
通常傅里叶变换(FT)只适合处理平稳信号,对于非平稳信号,由于频率特性会随时间变化,为了捕获这一时变特性,我们需要对信号进行时频分析,就包括短时傅里叶变换、小波变换、希尔伯特变换、希尔伯特黄变换这几种变换。
二.关于傅里叶变换(FT)
1.傅里叶变换定义
这里引用文章内容信号处理,引用自知乎
由于傅里叶变换都比较熟悉,这里定义不做赘述,傅里叶变换将函数 f(t) 分解成一系列复指数函数的加权和,利用它可以把复杂的时间信号和空间信号转换到频率域中,然后用频谱特性去分析和表示时域信号的特性。
首先考虑一个连续信号 f ( t ) f(t) f(t)的傅里叶变换和它的反变换,如下:
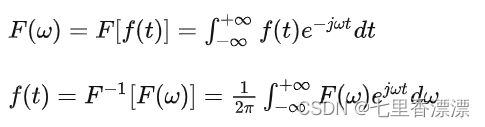
在实际应用中,计算机只能处理离散信号,所以对连续信号 x ( t ) x(t) x(t)进行时域采样,得到一组离散样本 x ( n ) x(n) x(n) ,对它进行傅里叶变换得到

上式即为离散时间傅里叶变换(DTFT),由于变换后得到的频域值仍然是连续的,我们继续对频域进行采样,得到

上式就是离散傅里叶变换(DFT),当前计算机中常用的快速傅里叶变换(FFT),就是DFT的快速算法。
2.傅里叶变换的缺陷
傅立叶分析有一个非常严重的缺点, 在将信号从时间域变换到频率域去的时候,把时间信息丢失了。 当我们在用傅立叶变化去分析一个具体信号的时候, 我们不知道哪个频率是对应在哪个时间点出现的,在哪个时间点消失的。
下面举例分析,如果一个信号的频率并不随着时间变化, 那么我们称它为平稳信号。而傅里叶变换就擅长分析平稳信号,因为频率并不随着时间变化。但是如果是非平稳信号用FT来进行分析呢?
case1.
x信号为平稳信号!
clc
clear
close all
fs = 1000;
t = 0:1/fs:1 - 1/fs;
x = [10 * cos(2 * pi * 10 * t)+ 20 * cos(2 * pi * 20 * t)+30 * cos(2 * pi * 30 * t)+40 * cos(2 * pi * 40 * t)];
figure;
plot(x)%时域图形,横轴为样本索引
fft1 = abs(fft(x))
figure;
%plot(abs(fft1))
%发现频谱对称,左边实频真实物理频率,右边虚频
L = length(fft1)
%2.横坐标频率化
f = fs*(1:(L/2))/L
figure;
plot(f,fft1(1:L/2))
%3.纵坐标量纲必须还原
%将频谱值除以频谱长度的一半,对称频谱中的一半(对称的一半)包含了完整的信息
plot(f,fft1(1:L/2)/(L/2))%绘制频谱图 幅频
绘制时域和频域的图像,它长这样:
时域:

频域:
由此可见,在频域图,FFT很好地显示了时域波形的频率分量,10,20,30,40Hz.
case2.
y信号为非平稳信号,但包含了x信号相同频率分量,代码如下:
fs = 1000;
t = 0:1/fs:1 - 1/fs;
%拼接四个信号,y 的持续时间是 4 秒,样本点之间的时间间隔是 1/fs 秒
y = [10 * cos(2 * pi * 10 * t), 20 * cos(2 * pi * 20 * t),30 * cos(2 * pi * 30 * t),40 * cos(2 * pi * 40 * t)];
figure;
plot(y)
fft1 = abs(fft(y))
figure;
plot(abs(fft1))
%发现频谱对称,左边实频真实物理频率,右边虚频
L = length(fft1)
%2.横坐标频率化
f = fs*(1:(L/2))/L
figure;
plot(f,fft1(1:L/2)/(L/2))
case3:
有意思的是,我们把时域信号倒放成z信号
fs = 1000;
t = 0:1/fs:1 - 1/fs;
%拼接四个信号,y 的持续时间是 4 秒,样本点之间的时间间隔是 1/fs 秒
y = [10 * cos(2 * pi * 10 * t), 20 * cos(2 * pi * 20 * t),30 * cos(2 * pi * 30 * t),40 * cos(2 * pi * 40 * t)];
z = y(end:-1:1)%倒放,-1步长
figure;
plot(z)
fft1 = abs(fft(y))
figure;
plot(abs(fft1))
%发现频谱对称,左边实频真实物理频率,右边虚频
L = length(fft1)
%2.横坐标频率化
f = fs*(1:(L/2))/L
figure;
plot(f,fft1(1:L/2)/(L/2))
时域:
频域:
对比case2,case3,不难发现,尽管这两个信号的时域分布完全相反,但是它们的频谱图是完全一致的。显然,FFT无法捕捉到信号在时域分布上的不同。
case4:
对x的平稳信号加一个高频突变信号,得到h信号
sharp = zeros(1,length(x));
% 给信号中间加一个突变
sharp(501:530) = 100 * cos(2*pi*100*linspace(0,10,30));
h = x + sharp;
时域:
频域:
对比想x,h两个信号的时域图,我们能很明显发现在第二个信号中央的部分出现了一个突变扰动。然而在频域图中,这样的变化并没有很好的被捕捉到。注意到红框中部分,显然傅里叶变换把突变解释为了一系列低成分的高频信号的叠加,并没有很好的反应突变扰动给信号带来的变化。实际上,时域信号只是多了一个高频分量。
对于信号中的突变,傅里叶变换很难及时捕捉。而在有些场合,这样的突变往往是十分重要的。总而言之,傅里叶变换非常擅长分析那些频率特征均一稳定的平稳信号。但是对于非平稳信号,傅立叶变换只能告诉我们信号当中有哪些频率成分——而这对我们来讲显然是不够的。我们还想知道各个成分出现的时间。知道信号频率随时间变化的情况,各个时刻的瞬时频率及其幅值——这也就是时频分析。(引用自此处)。
那么,短时傅里叶变换(STFT)来了!
三.关于短时傅里叶变换(STFT)理论
1.STFT定义
“把整个时域过程分解成无数个等长的小过程,每个小过程近似平稳,再傅里叶变换,就知道在哪个时间点上出现了什么频率了。”这就是短时傅里叶变换。
那么怎么一段一段处理呢?直接截取信号的一段来做 FFT 吗?一般我们通过加窗的方法来截取信号的片段。定义一个窗函数 w ( t ) w(t) w(t).
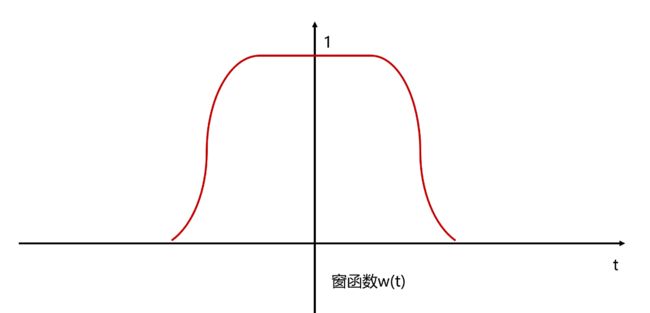
将窗函数位移到某一中心点 τ \tauτ,再将窗函数和原始信号相乘就可以得到截取后的信号 y(t)。
y ( t ) = x ( t ) ⋅ w ( t − τ ) y ( t ) = x ( t ) ⋅ w ( t − τ ) y ( t ) = x ( t ) ⋅ w ( t − τ ) y ( t ) = x ( t ) ⋅ w ( t − τ ) y(t) = x(t) \cdot \textrm{w}(t - \tau) y(t)=x(t)⋅w(t−τ) y(t)=x(t)⋅w(t−τ)y(t)=x(t)⋅w(t−τ)y(t)=x(t)⋅w(t−τ)
前面提到的直接截取的方法其实就是对信号加一个矩形窗,不过一般我们很少选用矩形窗,因为矩形窗简单粗暴的截断方法会产生的频谱泄露以及吉布斯现象,不利于频谱分析。更多关于窗函数的内容,可以看这里:加窗法。
2.STFT具体步骤及相关概念
1.STFT具体步骤
对原始信号 x ( t ) x(t)x(t) 做 STFT 的步骤如下:
首先将将窗口移动到信号的开端位置,此时窗函数的中心位置在 t = τ 0 t = \tau_0 t=τ0处,对信号加窗处理.
y ( t ) = x ( t ) ⋅ w ( t − τ 0 ) y(t)=x(t)⋅w(t−τ0) y(t)=x(t)⋅w(t−τ0)
然后进行傅里叶变换
X ( w ) = F ( y ( t ) ) = ∫ − ∞ + ∞ x ( t ) w ( t − τ 0 ) e ( − j w t ) d t X(w) = F(y(t)) = \int_{-\infty}^{+\infty}{x(t)w(t-\tau_0)e^{(-jwt)}dt} X(w)=F(y(t))=∫−∞+∞x(t)w(t−τ0)e(−jwt)dt
由此得到第一个分段序列的频谱分布 X ( ω ) X ( ω ) X(ω)。在现实应用中,由于信号是离散的点序列,所以我们得到的是频谱序列 X [ N ] 。
为了便于表示,我们在这里定义函数 S ( ω , τ ) S ( ω , τ ) S(ω,τ),它表示,在窗函数中心为 τ \tau τ 时,对原函数进行变换后的频谱结果 X ( ω ) X ( ω ) X(ω) ,即:
S ( ω , τ ) = F ( x ( t ) ⋅ w ( t − τ ) ) = ∫ − ∞ + ∞ x ( t ) w ( t − τ 0 ) e ( − j w t ) d t S ( ω , τ ) = F(x(t)⋅w(t−τ)) = \int_{-\infty}^{+\infty}{x(t)w(t-\tau_0)e^{(-jwt)}dt} S(ω,τ)=F(x(t)⋅w(t−τ))=∫−∞+∞x(t)w(t−τ0)e(−jwt)dt
对应到离散场景中, S [ ω , τ ] S [ ω , τ ] S[ω,τ] 就是一个二维矩阵,每一列代表了在不同位置对信号加窗,对得到的分段进行傅里叶变换后的结果序列。



2.时间分辨率和频率分辨率
2.1分辨率的影响因素
窗口的长度winlen会影响时间分辨率和频率分辨率。窗口越长,截取的信号越长(即选取点数nfft多),因为时间轴每格的长度即为窗函数的window length,时间轴格数越少,时间分辨率越低,也就是说分的帧:窗口越少!频率分辨率越高;窗口越短,截取的信号越短,时间分辨率越高,也就是说分的帧:窗口越多!频率分辨率越低,即频率轴间隔大!下面这个图就比较形象了!

如左图,若横轴(时间)共1.2s,纵轴(频率)共50Hz,横轴划分为12格,每格0.1s,纵轴划分为两格,每格25Hz;右图横轴每格0.3s,纵轴每格约8Hz。无论怎样划分,两图中每个方块的面积是相同的,且横轴划分格数越少(如右图,即选取的数据点数多),频率划分越细(如右图,相比左图划分两格,右图纵轴共6格)。
因此可得,时间轴分辨率与频率分辨率成反比。时间轴分辨率低(选取点数少),则频率分辨率高(如右图,能细致观察频率但时间轴无法准确估计);反之频率分辨率低(左图,时间轴可准确估计但频率只能观察0-25和25-50Hz两部分)。
在STFT中,频率分辨率是指能够分辨出的两个不同频率之间的最小间隔。频率分辨率取决于窗口的长度,即窗口内包含的时间段。较长的窗口可以提供更高的频率分辨率,因为更长的时间段内可以捕捉到更多的频率细节。
然而,较长的窗口长度会导致时间分辨率降低。时间分辨率是指能够分辨出信号中两个不同事件之间的最小时间间隔。当窗口长度增加时,窗口在时间域上的宽度增加,导致无法准确捕捉信号中短时变化的时间细节。因此,频率分辨率和时间分辨率在STFT中存在一种互相制约的关系。这也为后续介绍STFT的缺点进行铺垫。
2.2提高频率分辨率的方法
利用spectrogram函数自带两种提高频率分辨率的方法
方法1:将小于某个数值的数归零,提高频率分辨率。
调用格式:[S,F,T,P] = SPECTROGRAM(…,‘MinThreshold’,THRESH);当10*log10§的对应元素小于THRESH(以分贝为单位指定阈值)时,将P的元素设置为零。
方法2:利用功率谱将能量集中的原理,提高频率分辨率。
调用格式:[S,F,T,P] = SPECTROGRAM(…,‘reassigned’);将每个PSD估计值重新设定为其重心位置。
具体的spectrogram函数,以及stft函数在Matlab中的用法,下面会叙述。
四.STFT的MATLAB实现(非调用函数)
1.算法实现
STFT 的实现如下,算法返回的四个参数:
-
f 频率轴: m 维向量,表示傅里叶变换后每个点对应的频率值,单位为 Hz
若单边则频率轴:频率轴以模拟频率表示,其显示范围为采样频率的一半。 为什么呢?由傅里叶变换和采样定理知识我们可以知道,实信号经过傅里叶变换后频谱对称,实际信号频率范围其实只有采样频率一半。由于频率轴只显示采样频率一半,故其长度为nfft/2+1或(nfft+1)/2,分别对应nfft为even和odd。频率轴的分辨率受nfft的影响,为1/nfft*fs。
-t 时间轴 n 维向量,表示 n 个窗口中心时间 τ 1 \tau_1 τ1~ τ n \tau_n τn,单位为秒
在MATLAB中计算方式如下:
-
s: 一个二维矩阵 [m, n],每个列向量代表了在对应 τ \tau τ上 FFT 变换的结果
-
p: 一个二维矩阵 [m, n],每个列向量代表了 τ \tau τ上 的功率谱密度psd
-
实现函数mystft函数代码如下:
- function [s, f, t,p] = mystft(x, win, hop, nfft, fs)
% 计算短时傅里叶变换
% Input:
% x - 一维信号
% win - 窗函数
% hop - hop size,移动长度,帧移长度
% nfft - FFT points 计算FFT点数
% fs - 采样率
% Output:
% STFT - STFT-矩阵 [T, F]
% f - 频率向量
% t - 时间向量
% 信号转列向量,计算信号长度,窗长
x = x(:)
xlen = length(x);
wlen = length(win);
% 窗口数目 L
L = 1+fix((xlen-wlen)/hop);
if xlen%2==0
s = zeros(nfft/2+1, L);
else
s = zeros((nfft+1)/2, L);
end
% STFT
for l = 1:L%1窗到L窗循环
% 加窗
xw = x(1 + hop *(l- 1) : hop *(l - 1) + wlen).*win;%窗口化
%乘以窗口函数可以减小频谱泄漏的影响,使得频谱更准确地表示当前帧的特征。
% FFT计算
X = fft(xw, nfft);%计算每个窗口的fft
% X_centered = fftshift(X);如果想得到centered,需对频谱数据进行中心化处理
s(:, l) = X(1:nfft/2+1);%计算,单边,onesided,STFT矩阵,列数即帧数
% s(:, l) = X(1:nfft);%每帧fft,列数即帧数 这是双边,twosided
end
% 取每个窗口中点的时间点
t = (wlen/2:hop:wlen/2+(L-1)*hop)/fs;% 自己计算的时间轴,1/fs每个样本点时间间隔,取各窗口中心
f = (0:nfft/2+1-1)*(fs/nfft)% 自己计算的频率轴,长度nfft / 2+1或者(nfft+1)/2
% 频率 (fftshift之后的)
%f = (-nfft/2:nfft/2-1) * (fs/nfft);
%p:功率谱密度psd
k = 2/(fs*(window'*window))%变换系数k,弥补窗函数影响,这里为单边psd变换系数
%k = 1/(fs*(window'*window)) 此处为双边,因为单边除0和奈奎斯特频率外的所有频率的功率乘以2,以节省总功率。所以有个二倍关系
p = abs(s).*abs(s)*k;
end
- 下面生成三余弦波叠加信号:
clear;
clc;
close all;
% --------------------------------读取数据---------------------------
freq1 = 100; % First frequency component (Hz)
freq2 = 200; % Second frequency component (Hz)
freq3 = 300; % Third frequency component (Hz)
t = linspace(0, 1, 1000);
% 叠加
signal1 = sin(2 * pi * freq1 * t);
signal2 = sin(2 * pi * freq2 * t);
signal3 = sin(2 * pi * freq3 * t);
result = signal1 + signal2 + signal3;
result = abs(result);
sig = reshape(result, 1000, 1);%得到所需信号fs=1000Hz,持续时间一秒
- 使用自定义mystft函数并绘功率谱密度图
%绘制p功率谱密度 且以分贝形式显示
window = hann(256);
hop = 128;
nfft = 256;
fs = 1000;
subplot(121);
%绘制p功率谱密度 且以分贝形式显示
[s, f, t,p] = mystft(sig, window, hop, nfft, fs);
imagesc(t,f,10*log10(p));%10*log10() 将 PSD 值缩放到以分贝为单位,更好地可视化功率谱密度的相对强度
title('Draw with my.p');
xlabel('Time, s');
ylabel('Frequency, Hz');
h=colorbar;%添加一个颜色条,用于可视化功率/频率刻度。
h.Label.String = 'Power/Frequency(dB/Hz)'%颜色条标签
%绘制s,频谱图
subplot(122);
imagesc(t,f,abs(s));
title('Draw with my.s')
xlabel('Time, s');
ylabel('Frequency, Hz');
h=colorbar;%添加一个颜色条,用于可视化频谱幅度。
h.Label.String = 'Magnitude(dB)'%颜色条标签
在进行spectrogram函数进行绘图前,先主要介绍一下在MATLAB中的spectrogram函数!!本人在参加一个特征工程项目提取信号时频特征的时候,被MATLAB和python中实现STFT的不同函数,因参数或内部计算原理不同,所困惑!为此大费周章,通过读很多的大佬文档,对我所困惑内容进行汇总,以作纪念,这也是我第一次开始接触项目,从0学习代码。
2. 介绍MATLAB中 spectrogram函数 并绘图
1.Note: spectrogram()函数的句法和参数大概含义(物理意义和取值范围)可参考MATLAB help center。函数的底层代码可以在MATLAB命令行窗口输入open/eidt spectrogram 查看。
S = SPECTROGRAM(X),返回由矩阵S中的向量X指定的信号的短时傅立叶变换。默认情况下,X被分成8个有50个重叠的段,每个段用Hamming窗口加窗。用于计算离散傅里叶变换的频率点的数目等于256或大于段长度的下一次幂的256。如果X不能精确地分成八段,X将被截断。下面几种用法介绍如下:
- S = SPECTROGRAM(X,WINDOW),当WINDOW是一个向量时,将X分成与WINDOW长度相同的段,然后用WINDOW指定的向量对每个段进行加窗。如果WINDOW是一个整数,函数将X分成长度等于该整数值的段,并用Hamming窗口对每个段进行加窗。如果未指定WINDOW,则使用默认值。
- S = SPECTROGRAM(X,WINDOW,NOVERLAP),指定相邻线段之间重叠的NOVERLAP采样。如果WINDOW是整数,则NOVERLAP必须是小于WINDOW的整数。如果WINDOW是向量,则NOVERLAP必须是小于WINDOW长度的整数。如果未指定NOVERLAP,则使用默认值获得50个重叠。
- S = SPECTROGRAM(X,WINDOW,NOVERLAP,NFFT),指定用于计算离散傅里叶变换的频率点的数目。如果未指定NFFT,则使用默认NFFT。
- S = SPECTROGRAM(X,WINDOW,NOVERLAP,NFFT,Fs),指定采样率Fs(Hz)。如果Fs指定为空,则默认为1Hz。如果未指定,则使用归一化频率。
归一化频率:短时傅里叶变换中,归一化频率通常是指将频率值除以采样频率的一半,将其缩放到0到1的范围内。
那么为什么是一半呢?这是因为奈奎斯特采样定理,采样频率的一半被用作频率范围的上限,是由于采样定理要求至少以这个频率进行采样才能准确表示信号的最高频率。
S的每一列包含X的短期、时间局部化频率含量的估计值。S列中的时间从左到右递增。频率从0开始沿行递增。如果X是一个长度为NX的复信号,则 S是一个具有NFFT行和k=fix((NX-NOVERLAP)/(length(WINDOW)-NOVERLAP))列的复矩阵。 对于实X,如果NFFT是偶数,S有(NFFT/2+1)行;如果NFFT是奇数,S有(NFFT+1)/2行。
这里最着重介绍下面这两种调用方式:
-
SPECTROGRAM([S, F, T] = spectrogram(X,WINDOW,NOVERLAP,NFFT,Fs,“reassigned”,“onesided”,‘OutputTimeDimension’,‘downrows’);返回频率向量F和时间向量T,在该向量下计算频谱图。F的长度等于S的行数。T的长度为k(如上定义),其值对应于每个线段的中心。如果没有提供采样率,F包含归一化频率。
“reassigned”,设定为其重心位置,可以不选,Default默认不选
矩阵S中的向量X指定的信号的短时傅立叶变换,默认返回单边频谱"onesided",也可以改为’twosided’双边,"centered"中心对称
‘OutputTimeDimension’,‘downrows’:使得S的时间维度跨行,如果为空,默认值是跨列的’acrosscolumns’[S, F, T, P] = spectrogram(X,WINDOW,NOVERLAP,NFFT,Fs,“twosided”,“psd”,‘OutputTimeDimension’,‘downrows’);P是表示每段功率谱密度(PSD)的矩阵。对于实信号,SPECTROGRAM返回每段PSD的单边修正周期图估计值;对于复信号,如果指定了频率向量,则返回双边PSD。
“psd"默认P返回psd功率谱密度,也可改为"power"返回功率谱
矩阵S中的向量X指定的信号的短时傅立叶变换,矩阵P中的向量X指定的信号的功率谱密度或者功率谱,默认返回单边频谱"onesided”,也可以改为’twosided’双边,"centered"中心对称.
值得注意的是!
[S,F,T,P]=spectrogram(x,window,noverlap,nfft,fs) %有返回值
spectrogram(x,window,noverlap,nfft,fs,‘yaxis’) %无返回值调用,直接输出图形,**这里的是psd功率谱密度,也就是10*log10§!!**也就是说当函数spectrogram()直接调用时输出的是以分贝值表示的PSD
- 使用MATLAB中 spectrogram函数 并绘图
%绘制spectrogram.p功率谱密度 且以分贝形式显示
subplot(121);
%绘制p功率谱密度 且以分贝形式显示
[s, f, t,p] = spectrogram(sig,hann(256),128,256,1000,"onesided","psd",'OutputTimeDimension','downrows');
imagesc(t,f,10*log10(p));%10*log10() 将 PSD 值缩放到以分贝为单位,更好地可视化功率谱密度的相对强度
title('Draw with spec.p')
xlabel('Time, s');
ylabel('Frequency, Hz');
h=colorbar;%添加一个颜色条,用于可视化功率/频率刻度。
h.Label.String = 'Power/Frequency(dB/Hz)'%颜色条标签
%绘制s,频谱图
subplot(122);
imagesc(t,f,abs(s));
title('Draw with spec.s')
xlabel('Time, s');
ylabel('Frequency, Hz');
h=colorbar;%添加一个颜色条,用于可视化频谱幅度。
h.Label.String = 'Magnitude(dB)'%颜色条标签
由此对比自己写的mystft函数与MATALB中spectrogram绘制无论psd,或者频谱图,图形大致相同!
2.如何根据绘制图形理解返回参数!
-
第一 关于返回参数s和p的关系
S为信号x进行n次快速傅里叶变换后的结果,为一复数矩阵,横向按时间递增,纵向按频率递增。包含nfft/2+1或(nfft+1)/2行、n列,推导见前述。P为信号的功率谱密度,为一实矩阵,维数与S保持一致。
由信号分析的知识可以知道,功率谱密度可以由信号的快速傅里叶变换结果的绝对值平方除以信号长度表示,但是在这里,为了弥补窗函数的影响,还需要添加一个变换系数k。即

这里为什么有一个2呢对于单边psd来说,这是因为,单边除0和奈奎斯特频率外的所有频率的功率乘以2,以节省总功率。所以有个二倍关系!
那为什么除0频率呢?这是因为0频率是唯一一个没有对称的频率分量,它只存在于单边频谱的一侧。将0频率的功率乘以2会导致其能量被计算两次,从而引入冗余。因此,在计算单边频谱时,0频率的功率不需要乘以2,以避免重复计算和浪费功率。
在本节1算法实现中中便有根据s求p的代码! -
第二 关于返回参数 t 时间轴
我们已经知道输出的图像时间轴分辨率受制于窗口大小Nw和重叠长度noverlap,其长度为k。t中的数值为每个segment的中间值,什么意思呢?这里的segment理解为加的窗口,以本文中的程序为例,我使用的是采样频率为1000Hz的1s信号,窗口长度Nw为256,noverlap为128。那么t的第一个数据该是多少?即1/1000 * 256/2 = 0.128s,而后每次递增1/1000 *(Nw - noverlap)= 0.008s。注意hopsize = Nw - noverlap,也就是帧移。
3.MTALAB 中的stft函数
stft函数与spectrogram函数作用大致相同,只是默认参数不同
例如
[s, f, t] = stft(sig,1000,“Window”,hann(256),“OverlapLength”,128,“FFTLength”,256)
[s, f, t,p] = spectrogram(sig,hann(256),128,256,1000,“psd”);
此处,
1.stft 默认其他参数’centered’输出对称双边谱 ,而spectrogram默认’onesided’,单边谱
2.要注意的是直接绘图,两者都可以绘制功率谱密度图形,但是 spectrogram 还可以输出功率谱,而 stft 就不行了,stft只能输出功率谱密度!!!
3.stft函数调用虽然可以直接执行绘制功率谱密度图形,但是他的语法并没有返回参数p这一功能
主要以上三点区别,在我工作时,让我疑惑,其他的可以help 在MATLAB解决,其他应该问题不大!
五.关于python中实现STFT的函数
由于我接触短时傅里叶变换时,需要完成的任务是,提取一个示例信号的时频特征,要求在python,MATLAB,C++上面实现,在python实现过程中,几经波折,发现一直与MATLAB的结果不同,对此我深感疑惑,翻阅很多相关文档,但是还是百思不得其解,深入内部研究,最终发现还是因为一些参数的不同,以及相关计算原理的略微差别导致的。
最后一句话!还是官方文档描述清楚的多,还是要耐着性子多看官方文档!
在Python中,我所使用实现STFT的函数有两个:
- scipy库中signal.stft函数:
- matplotlib库中mlab.specgram函数
在这里主要介绍下参数以及我感觉比较模糊的几个点吧:
1.scipy.signal.stft函数
详细内容请参考scipy.stft官方文档:
scipy.signal.stft(x, fs=1.0, window=‘hann’, nperseg=256, noverlap=None, nfft=None, detrend=False, return_onesided=True, boundary=‘zeros’, padded=True, axis=- 1,scaling=‘spectrum’)
上述引用的是默认参数!
参数:
x: array_like
测量值的时间序列,也就是信号
fs: 浮点数,可选
x 时间序列的采样频率。默认为 1.0。
window: str 或 tuple 或 数组,可选
想要使用的窗口。如果窗户是一个字符串或元组,它被传递给scipy.signal.get_window生成窗口值,默认为DFT-even。看scipy.signal.get_window获取窗口列表和所需参数。如果窗户是数组,它将直接用作窗口,其长度必须为nperseg。默认为 Hann 窗口。
nperseg: int 可选
每个段的长度。默认为 256。
noverlap: int 可选
段之间重叠的点数。如果None,noverlap = nperseg // 2.默认为None.指定时,必须满足 COLA 约束(请参阅下面的注释)。
nfft: int 可选
如果需要零填充 FFT,则使用的 FFT 的长度。如果没有,FFT 长度为 nperseg。默认为无。
detrend: str 或函数 或False, 可选的(这个我不知道啥意思,就按默认的来,不执行趋势消除操作)
指定如何去除每个段的趋势。如果scipy.signal.detrend是一个字符串,它作为类型参数scipy.signal.detrend函数。如果它是一个函数,它接受一个段并返回一个去趋势的段。如果scipy.signal.detrend是False,没有去趋势。默认为False.
return_onesided: 布尔型,可选
如果为真,则返回真实数据的one-sided 频谱。如果 False 返回 two-sided 频谱。默认为 True,但对于复杂数据,始终返回 two-sided 频谱。
boundary: str 或无,可选
指定输入信号是否在两端扩展,以及如何生成新值,以使第一个窗口段居中于第一个输入点。这具有在所采用的窗口函数从零开始时能够重建第一个输入点的好处。有效选项是 [‘even’, ‘odd’, ‘constant’, 'zeros’, None] 。默认为‘zeros’,用于零填充扩展。 IE。 [1, 2, 3, 4] 扩展为 [0, 1, 2, 3, 4, 0] 对于 nperseg=3 。
这个参数就是导致我在python中得到的时间轴T与MATLAB不一样的原因a:MATLAB没有boundary这个参数,也就是None!导致python多了两个时间轴
padded: 布尔型,可选
指定输入信号是否在末尾补零以使信号完全适合整数个窗口段,以便所有信号都包含在输出中。默认为真。填充发生在边界扩展之后,如果边界不是"None",并且填充为“True”(默认情况下),则填充发生在边界扩展之后。
这个参数就是导致我在python中得到的时间轴T与MATLAB不一样的原因b:MATLAB同样没有padded这个参数,也就是None!,若默认True则1000长度扩展为1024,被窗长256整除。
axis: int 可选
计算 STFT 的轴;默认值在最后一个轴上(即 axis=-1 )。
scaling: {‘spectrum’, ‘psd’}(有的scipy版本没有这个参数,只能输出STFT频谱,需要升级版本,我这里版本就没有这个参数)
默认的’‘spectrum’'Zxx的每条频率线被解释为幅度频谱。
“psd”选项将每条线缩放到功率谱密度,它允许通过在abs(Zxx)**2上进行数字积分来计算信号的能量。而使用 “psd” 缩放选项时,Zxx 表示功率谱密度。每个频率线经过缩放,可以通过对 abs(Zxx)**2 进行数值积分来计算信号的能量或进行功率谱密度分析。
返回:
f: ndarray
采样频率数组。
t: ndarray
分段时间数组。
Zxx: ndarray
x 的 STFT时频数据。默认情况下,Zxx 的最后一个轴对应分段时间。
这点也是困扰我很久!!!
就是为啥子我在python 使用下面这段signal.stfth函数:
f, t, amp = signal.stft(Signal,1000,'hann',256,128,256,detrend=False,return_onesided=True,boundary=None,padded=False)
得到的amp的输出,和我在MATLAB使用spectrogram函数得到的S同样都表示信号的短时傅里叶变换频谱,值却差了几十倍,不过大致形状一致!对比如下:
这是signal.stft 输出的abs(amp)幅度谱,同样使用的信号都是本文上面产生的三余弦波叠加信号。

而在MATLAB中保持参数一样使用代码:
[S, F, T, P] = spectrogram(Signal,window,128,256,1000,"onesided","power",'OutputTimeDimension','downrows');
z = abs(S);

两者对比发现,差的离谱,这也是我当时困惑不已的问题!
那么我把MATLAB中短时傅里叶频谱
[S, F, T, P] = spectrogram(Signal,window,128,256,1000,“onesided”,“power”,‘OutputTimeDimension’,‘downrows’);
z = abs(S);
返回的S也就是短时傅里叶变换频谱数据z打印出来:
114.4347 116.6547 116.0653 115.0360 116.2669 116.5448 57.7140 58.8103 58.4488 57.5992
列 11 至 20
58.4890 58.7674 0.3629 0.2827 0.2328 0.2112 0.1571 0.2886 0.0949 0.0682
列 21 至 30
0.0419 0.1547 0.0856 0.0780 0.0427 0.0252 0.0418 0.0493 0.0524 0.0370
列 31 至 40
0.0245 0.0144 0.0276 0.0432 0.0101 0.0219 0.0162 0.0126 0.0074 0.0273
列 41 至 50
0.0255 0.0146 0.0118 0.0102 0.0084 0.0175 0.0129 0.0107 0.0093 0.0062
列 51 至 60
0.0098 0.0181 0.0106 0.0084 0.0079 0.0017 0.0028 0.0083 0.0150 0.0072
列 61 至 70
0.0072 0.0025 0.0049 0.0138 0.0050 0.0068 0.0071 0.0046 0.0065 0.0048
列 71 至 80
0.0133 0.0070 0.0076 0.0048 0.0021 0.0131 0.0111 0.0077 0.0087 0.0048
列 81 至 90
0.0085 0.0061 0.0100 0.0092 0.0105 0.0079 0.0123 0.0156 0.0180 0.0114
列 91 至 100
0.0132 0.0132 0.0105 0.0127 0.0128 0.0146 0.0174 0.0190 0.0182 0.0229
列 101 至 110
0.0246 0.0194 0.0239 0.0249 0.0305 0.0269 0.0304 0.0265 0.0343 0.0341
列 111 至 120
0.0369 0.0421 0.0365 0.0379 0.0522 0.0536 0.0556 0.0623 0.0700 0.0572
列 121 至 130
0.0854 0.0939 0.1063 0.1032 0.0915 0.0930 0.1551 0.1761 0.1853 0.1880
列 131 至 140
0.1875 0.1682 0.3299 0.3724 0.3711 0.4048 0.3989 0.3578 0.9308 1.0372
列 141 至 150
1.1236 1.1508 1.0568 1.0127 5.3117 5.9876 6.9273 7.1017 6.8514 5.8632
列 151 至 160
37.6415 41.2000 44.2039 44.9128 43.8176 40.5416 45.2350 48.8751 50.9936 51.3903
列 161 至 170
50.7874 48.2288 12.4145 13.2013 13.2123 13.1210 13.2966 13.0551 1.3118 1.4198
列 171 至 180
1.5259 1.5164 1.5022 1.3995 0.4069 0.4362 0.4649 0.4728 0.4283 0.4356
列 181 至 190
0.1782 0.1866 0.1919 0.2095 0.2160 0.1908 0.0937 0.0982 0.1120 0.1103
列 191 至 200
0.1022 0.0999 0.0553 0.0611 0.0691 0.0656 0.0596 0.0583 0.0354 0.0413
列 201 至 210
0.0369 0.0408 0.0451 0.0366 0.0241 0.0278 0.0271 0.0297 0.0202 0.0242
列 211 至 220
0.0172 0.0181 0.0238 0.0176 0.0219 0.0167 0.0128 0.0127 0.0143 0.0172
列 221 至 230
0.0126 0.0118 0.0099 0.0111 0.0090 0.0077 0.0080 0.0086 0.0080 0.0106
列 231 至 240
0.0118 0.0116 0.0101 0.0064 0.0067 0.0093 0.0099 0.0062 0.0002 0.0047
列 241 至 250
0.0059 0.0070 0.0043 0.0077 0.0067 0.0034 0.0056 0.0054 0.0075 0.0111
列 251 至 260
0.0031 0.0021 0.0058 0.0070 0.0118 0.0042 0.0081 0.0015 0.0067 0.0105
列 261 至 270
0.0100 0.0190 0.0021 0.0030 0.0086 0.0140 0.0088 0.0112 0.0152 0.0063
列 271 至 280
0.0123 0.0172 0.0248 0.0326 0.0187 0.0119 0.0197 0.0225 0.0405 0.0444
列 281 至 290
0.0253 0.0224 0.0363 0.0420 0.0526 0.0649 0.0781 0.0451 0.0811 0.1088
列 291 至 300
0.1478 0.2143 0.1112 0.1071 0.2554 0.3887 0.5877 0.2903 0.5352 0.3624
列 301 至 310
3.7810 6.4916 8.2561 9.7508 7.9905 5.9877 8.8076 16.9258 23.2995 26.3018
列 311 至 320
22.2838 15.4811 6.2451 11.5171 16.3487 18.5667 15.5885 10.5517 0.9772 1.1718
列 321 至 330
1.6297 2.1085 1.6276 1.1317 0.1766 0.2318 0.3133 0.2278 0.2509 0.2159
列 331 至 340
0.0625 0.0913 0.0925 0.1568 0.1088 0.0791 0.0291 0.0457 0.0529 0.0587
列 341 至 350
0.0587 0.0383 0.0158 0.0236 0.0372 0.0377 0.0180 0.0218 0.0095 0.0117
列 351 至 360
0.0169 0.0307 0.0242 0.0139 0.0061 0.0071 0.0098 0.0102 0.0089 0.0096
列 361 至 370
0.0041 0.0068 0.0130 0.0184 0.0085 0.0069 0.0030 0.0067 0.0088 0.0017
列 371 至 380
0.0087 0.0051 0.0023 0.0056 0.0027 0.0112 0.0018 0.0039 0.0021 0.0038
列 381 至 390
0.0069 0.0040 0.0056 0.0030 0.0022 0.0021 0.0078 0.0061 0.0044 0.0026
列 391 至 400
0.0026 0.0027 0.0034 0.0060 0.0042 0.0028 0.0033 0.0049 0.0049 0.0025
列 401 至 410
0.0037 0.0036 0.0043 0.0068 0.0098 0.0076 0.0085 0.0048 0.0058 0.0077
列 411 至 420
0.0085 0.0050 0.0025 0.0066 0.0081 0.0078 0.0060 0.0111 0.0127 0.0092
列 421 至 430
0.0119 0.0097 0.0187 0.0139 0.0168 0.0132 0.0186 0.0189 0.0281 0.0233
列 431 至 440
0.0147 0.0202 0.0317 0.0381 0.0295 0.0401 0.0520 0.0339 0.0617 0.0763
列 441 至 450
0.0768 0.0812 0.0592 0.0656 0.1489 0.1777 0.2347 0.2013 0.2058 0.1601
列 451 至 460
0.5365 0.6753 0.8937 0.9551 0.9576 0.6194 15.9767 16.3373 17.3106 17.4329
列 461 至 470
17.2693 16.1165 27.2982 27.4054 28.2265 28.1378 28.1902 27.2131 11.5127 11.4101
列 471 至 480
11.5526 11.2908 11.6385 11.3664 0.4443 0.4651 0.4739 0.5216 0.3981 0.4499
列 481 至 490
0.1134 0.1183 0.0965 0.1312 0.1169 0.1161 0.0445 0.0418 0.0509 0.0539
列 491 至 500
0.0629 0.0456 0.0215 0.0181 0.0340 0.0263 0.0102 0.0217 0.0119 0.0126
列 501 至 510
0.0130 0.0151 0.0203 0.0113 0.0073 0.0110 0.0060 0.0080 0.0083 0.0060
列 511 至 520
0.0051 0.0089 0.0104 0.0075 0.0062 0.0031 0.0042 0.0062 0.0079 0.0020
列 521 至 530
0.0063 0.0020 0.0042 0.0038 0.0019 0.0057 0.0048 0.0025 0.0048 0.0042
列 531 至 540
0.0052 0.0041 0.0047 0.0035 0.0058 0.0065 0.0083 0.0046 0.0041 0.0047
列 541 至 550
0.0073 0.0084 0.0060 0.0087 0.0084 0.0060 0.0095 0.0093 0.0049 0.0024
列 551 至 560
0.0019 0.0077 0.0125 0.0097 0.0121 0.0149 0.0125 0.0100 0.0169 0.0125
列 561 至 570
0.0146 0.0033 0.0120 0.0136 0.0238 0.0198 0.0131 0.0249 0.0153 0.0193
列 571 至 580
0.0349 0.0312 0.0260 0.0173 0.0315 0.0287 0.0542 0.0470 0.0444 0.0440
列 581 至 590
0.0303 0.0451 0.0909 0.0729 0.0586 0.0609 0.0723 0.0762 0.1701 0.1308
列 591 至 600
0.1094 0.0969 0.1212 0.1430 0.3788 0.2944 0.2736 0.2659 0.2401 0.3174
列 601 至 610
1.1653 0.9135 0.7597 0.4534 0.8285 0.9646 9.2317 6.7258 3.7148 3.7461
列 611 至 620
4.2021 7.2030 39.7972 31.0552 23.5289 22.2872 24.5615 32.6867 37.3440 30.4368
列 621 至 630
25.7522 24.9904 26.3127 31.6816 6.8808 6.0131 5.8337 6.2336 5.8048 6.1734
列 631 至 640
1.0433 0.8837 0.7728 0.6209 0.7760 0.9131 0.3538 0.3027 0.2601 0.2899
列 641 至 650
0.2970 0.3070 0.1621 0.1429 0.1323 0.1024 0.1125 0.1403 0.0876 0.0774
列 651 至 660
0.0648 0.0638 0.0666 0.0761 0.0525 0.0438 0.0332 0.0433 0.0444 0.0463
列 661 至 670
0.0339 0.0263 0.0285 0.0181 0.0184 0.0305 0.0230 0.0185 0.0202 0.0241
列 671 至 680
0.0220 0.0214 0.0161 0.0151 0.0093 0.0036 0.0106 0.0157 0.0116 0.0120
列 681 至 690
0.0101 0.0143 0.0084 0.0119 0.0084 0.0084 0.0108 0.0021 0.0100 0.0093
列 691 至 700
0.0061 0.0051 0.0053 0.0081 0.0007 0.0074 0.0043 0.0036 0.0044 0.0042
列 701 至 710
0.0065 0.0061 0.0028 0.0044 0.0084 0.0037 0.0058 0.0054 0.0014 0.0055
列 711 至 720
0.0066 0.0053 0.0028 0.0052 0.0007 0.0065 0.0022 0.0016 0.0066 0.0058
列 721 至 730
0.0023 0.0071 0.0102 0.0068 0.0099 0.0073 0.0050 0.0072 0.0143 0.0071
列 731 至 740
0.0001 0.0100 0.0093 0.0094 0.0092 0.0132 0.0209 0.0151 0.0176 0.0210
列 741 至 750
0.0237 0.0227 0.0257 0.0252 0.0365 0.0508 0.0637 0.0465 0.0383 0.0488
列 751 至 760
0.0929 0.1319 0.1201 0.1132 0.1574 0.1199 0.3817 0.5161 0.3884 0.5058
列 761 至 770
0.3920 0.4833 12.4744 8.6464 4.3326 2.1490 5.0213 9.4463 24.4115 16.5152
列 771 至 774
7.7250 0.8213 9.3013 18.1664
**问题来啦!!!**上文所述,MATLAB给出的幅频数据,代表每一个频率对信号幅值的贡献,我这里所使用的三余弦波叠加信号,最高幅度也不超过3。
三余弦波叠加信号部分代码
clear;
clc;
close all;
% --------------------------------读取数据---------------------------
freq1 = 100; % First frequency component (Hz)
freq2 = 200; % Second frequency component (Hz)
freq3 = 300; % Third frequency component (Hz)
t = linspace(0, 1, 1000);
% 叠加
signal1 = sin(2 * pi * freq1 * t);
signal2 = sin(2 * pi * freq2 * t);
signal3 = sin(2 * pi * freq3 * t);
result = signal1 + signal2 + signal3;
result = abs(result);
sig = reshape(result, 1000, 1);%得到所需信号fs=1000Hz,持续时间一秒
明显MATLAB计算幅频值不对!我查阅B站看到一个up主解释MATLAB关于幅频值的绘制【NO.5 傅里叶变换频谱图你有多了解-哔哩哔哩】知道所以然:这是因为MATLAB中fft函数的特性所决定的,因此绘制幅频图时,必须要采取一个办法的他的量纲进行还原,也就是对纵坐标进行还原。还原方法就是除以FFT数据长度的一般就可以啦!因此在MATLAB代码添加
S = S/((length(window)/2))
最终可以绘制与Python中scipy.signal.stft函数一致的幅频特征图!!!!

2.matplotlib.specgram函数
详细文档见.matplotlib.specgram官方文档
这里不多说了,官方文档写的还是很详细的。
我发现和MATLAB中spectrogram函数的不同之处就是:
S,F,T = mlab.specgram(Signal, NFFT=256, Fs=1000, window=window, noverlap=128, mode='psd',sides='onesided')
返回参数只有三个S,F,T.mode = 可以为’psd’:返回S,功率谱密度,'complex’返回S,短时傅里叶变换结果,注意!这里的频谱不用还原量纲,而MATLAB就需要!!!!!还有’angle’和’phase’参数,见官方文档。
最后写出我提取信号特征(信号STFT幅频值)使用的代码:
pthon代码:
#==============时频原子特征特征=============#
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
from tqdm import tqdm
def STFT( Signal):
f, t, amp = signal.stft(Signal,1000,'hann',256,128,256,detrend=False,return_onesided=True,boundary=None,padded=False)
z = abs(amp.copy())
return z
def tf_feature(X):
for index, data in tqdm(enumerate(X)): # 用于对 self.X 中的每个元素进行迭代。enumerate() 函数用于将列表或数组中的元素和它们的下标一起返回。
data = abs(data) # data 数组中的所有元素取绝对值
if index == 0:
print(STFT(data))
feature_temp = STFT(data).reshape(-1) # STFT() 计算信号的 STFT 幅度谱。将幅度谱转化为一维数组
feature_temp = np.expand_dims(feature_temp, axis=0) # 使feature扩展为二维
else:
feature_temp = np.vstack(
(feature_temp, STFT(data).reshape(-1))) # 如果不是第一个元素,将一维数组添加到 feature_temp 数组的末尾
return feature_temp
# def custom_print(data):
# for item in feature:
# print(item)
# ---------------------------------------------------读取数据---------------------------------------------------------- #
print('--------------------------------read data---------------------------')
# 定义三个频率分量的参数
freq1 = 100 # 第一个频率分量的频率(Hz)
freq2 = 200 # 第二个频率分量的频率(Hz)
freq3 = 300 # 第三个频率分量的频率(Hz)
t = np.linspace(0,1,1000)
# 生成三个频率分量的正弦波信号
signal1 = np.sin(2 * np.pi * freq1 * t)
signal2 = np.sin(2 * np.pi * freq2 * t)
signal3 = np.sin(2 * np.pi * freq3 * t)
# 将三个频率分量的信号相加
result = signal1 + signal2 + signal3
# with open('result.txt', 'w') as f:
# for i in range(len(result)):
# f.write(str(result[i]) + '\n') //将result数据保存到txt文本
# 训练数据和标签
train_X = result.reshape((1,1000))# 数据,信号变形为包含单个样本和 1000 个特征值的二维数组.行代表样本,列特征
train_Y = np.array([0])#标签,标签被设置为 0
print(train_X.shape)
plt.plot(result)
plt.show()
plt.savefig(r'.\signal.png')
# ---------------------------------------------循环遍历每一条数据提取特征-------------------------------------------------- #
print('----------------------------feature process-------------------------')
feature = tf_feature(train_X)
print(feature)
# with open('feature.txt', 'w') as f:
# for i in range(len(feature)):
# f.write(str(feature[i]) + '\n') #将feature数据保存到txt文本
# print(feature.shape)
# print(len(feature))
# File name #
Filename = 'test'
# -------------绘制特征图------------- #
print('----------------------------plot feature-------------------------')
plt.plot(feature[0])
plt.xlabel("index")
plt.ylabel("Magnitude")
plt.title('scipy.signal.stft')
plt.show()
plt.savefig(r'.\{}-feature2.png'.format(Filename))
MTLAB代码:
clc
clear
close all
% Read data
disp('--------------------------------read data---------------------------');
freq1 = 100; % First frequency component (Hz)
freq2 = 200; % Second frequency component (Hz)
freq3 = 300; % Third frequency component (Hz)
t = linspace(0, 1, 1000);
% Generate three sinusoidal signals
signal1 = sin(2 * pi * freq1 * t);
signal2 = sin(2 * pi * freq2 * t);
signal3 = sin(2 * pi * freq3 * t);
% Combine the signals
result = signal1 + signal2 + signal3;
% Reshape result for training
train_X = reshape(result, 1,1000);% Transpose the result to make it a row vector
disp(train_X)
% Print shape of train_X
disp('--------------------------Print shape of train_X-------------------------');
disp(size(train_X));
% Plot the signal
disp('----------------------------plot signal-------------------------');
figure();
plot(result);
saveas(gcf, 'signal.png');
% Feature extraction
disp('----------------------------feature process-------------------------');
feature_temp = tf_feature(train_X);
feature = feature_temp(1, :);
disp(feature);
disp(length(feature));
% Save feature plot
disp('----------------------------save feature plot-------------------------');
figure();
plot(feature);
xlabel('index');
ylabel('Magnitude');
title('MATLAB.spectrogram')
saveas(gcf, 'test-feature2.png');
%STFT function
function z = STFT(Signal)
window = hann(256);
[S, F, T, P] = spectrogram(Signal,window,128,256,1000,"onesided","power",'OutputTimeDimension','downrows');
S = S/((length(window)/2))%幅频量纲进行还原
z = abs(S);
%S返回则表示频谱
%'psd'将返回功率谱密度。
%指定'power',则P返回功率谱。
end
%tf_feature function
function feature_temp = tf_feature(X)
for index = 1:size(X, 1)
data = abs(X);
if index == 1
disp(data);
% B = STFT(data);
feature_temp = reshape(STFT(data), 1, []);
else
feature_temp = [feature_temp; reshape(STFT(data), 1, [])];
end
end
end
C++代码
#include 类型变量 frame存储当前帧
for (int j = 0; j < frameSize; j++)
{
frame[j] = signal[start + j] * window[j];
}
// 填充输入数据
for (int j = 0; j < frameSize; j++)
{
fftInput[j][0] = frame[j];//fftInput 中的实部
fftInput[j][1] = 0.0;//fftInput 中的虚部
}
// 执行FFT
fftw_execute(fftPlan);
// 提取幅度谱
//double h = 2.0 / (fs * dotProduct(window, window));//可以提取功率谱的系数
for (int k = 0; k <= windowSize / 2; k++)
{
double real = fftOutput[k][0];
double imag = fftOutput[k][1];
double amplitude = sqrt(real * real + imag * imag);
stft[i][k] = sqrt(real * real + imag * imag)/(windowSize / 2);//量纲化幅频
/* stft[i][k] = amplitude * amplitude * h; */ //功率谱密度
}
}
fftw_destroy_plan(fftPlan);
fftw_free(fftInput);
fftw_free(fftOutput);
return stft;
}
// STFT函数
vector<vector<double>> STFT(const vector<double>& signal)
{
WindowType windowType = HANN;
int windowSize = 256; // 窗口大小
int overlap = 128; // 重叠大小
vector<double> window = getWindow(windowType, windowSize);
return calculateSTFT(signal, window, overlap,1000);
}
// tf_feature函数
vector<vector<double>> tf_feature(const vector<vector<double>>& X)
{
vector<vector<double>> features;
for (int index = 0; index < X.size(); index++)//X.size()二维数组中一维向量的数量
{
vector<double> data(X[index].size());
for (int i = 0; i < X[index].size(); i++)
{
data[i] = abs(X[index][i]);
}
vector<vector<double>> stft = STFT(data);
if (index == 0)
{
features = stft;
}
else
{
for (int i = 0; i < stft.size(); i++)
{
features[i].insert(features[i].end(), stft[i].begin(), stft[i].end());//逐行表样本添加特征
}
}
}
return features;
}
int main()
{
// 读取文件数据,即示例信号输出数据result
ifstream infile;//创建流对文件
infile.open("F:\\桌面\\fftw\\result.txt", ios::in);//打开文件
if (!infile.is_open())//判断是否打开成功
{
cout << "读取文件失败" << endl;
return 0;
}
string buf;//定义字符串buf
vector<double> result(1000);
int i = 0;
while (getline(infile, buf))//逐行读取数据存储到字符换buf
{
result[i] = stod(buf);//stod函数转换为double类型存储至result向量
i++;
}
// 训练数据和标签
vector<vector<double>> train_X{ result };
vector<int> train_Y{ 0 };
// 提取特征
vector<vector<double>> feature = tf_feature(train_X);
// 输出特征值
for (int i = 0; i <feature.size(); i++)
{
for (int j = 0; j < feature[i].size(); j++)
{
cout << feature[i][j]<<" ";
}
cout<<endl;
}
cout << endl;
//输出数据第二种方式
//for (const auto& f : feature)
//{
// for (const auto& val : f)
// {
// cout << val << " ";
// }
// cout << endl;
//}
return 0;
}
七.短时傅里叶变换(STFT)的缺点(非调用函数)
如果你仔细分析上面的内容,你会发现短时傅立叶变换也有不容忽视的缺陷。在介绍频率分辨率和时间分辨率,已经做了铺垫,时间分辨率与频率分辨率存在制衡问题!
最明显的一个问题:窗口的宽度该设多少为好呢?为了阐明这个问题的影响,我们做这么一个实验:调整不同 wlen 的值,来看看影响。
clear;
clc;
close all;
% --------------------------------读取数据---------------------------
freq1 = 100; % First frequency component (Hz)
freq2 = 200; % Second frequency component (Hz)
freq3 = 300; % Third frequency component (Hz)
t = linspace(0, 1, 1000);
% 叠加
signal1 = sin(2 * pi * freq1 * t);
signal2 = sin(2 * pi * freq2 * t);
signal3 = sin(2 * pi * freq3 * t);
result = signal1 + signal2 + signal3;
result = abs(result);
sig = reshape(result, 1000, 1);%得到所需信号fs=1000Hz,持续时间一秒
len = [32, 64, 128, 256];
fs = 1000;
for i = 1:4
wlen = len(i);
noverlap = wlen/2;
nfft = wlen;
win = blackman(wlen, 'periodic');
subplot(2, 2, i);%绘制四个不同窗长图
spectrogram(sig, win, noverlap, nfft, fs);
title(sprintf('Wlen = %d',wlen));%sprintf格式化字符串
end
- 窗太窄,窗内的信号太短,会导致频率分析不够精准,频率分辨率差,具体表现是黄色的竖线越来越宽、越来越模糊
- 窗太宽,时域上又不够精细,时间分辨率低,具体表现是淡蓝色的横线越来越宽、越来越模糊(还记得吗,竖线表示交界处的突变造成的高频干扰成分)
下面时域举个例子
固定的窗口大小过于死板。对低频信号(大周期)而言,有可能连一个周期都不能覆盖,这导致低频处相对时间分辨率很高,相对频率分辨率很低!
对高频信号而言,可能覆盖过多周期,不能反映信号变化。这导致低频处相对时间分辨率很高,相对频率分辨率很低!

可见,对于帧长固定的短时傅里叶变换,在全局范围内的时间分辨率和频率分辨率是固定的。如果我们想要在低频区域具有高频率分辨率,在高频区域具有高时间分辨率,显然STFT是不能满足要求的。那么后话我的搜索解决方法,引入另一种时频分析方法——小波变换。那都是后话了~
八.声明
本文章自用,是本人在学习工作中,针对自己使用STFT相关函数工具时遇到的困难,不解,经过阅读相关STFT文档所汇总的内容!初学,以此作为笔记使用!!感谢各位大佬指正!
参考文献
[1]时频分析之STFT:短时傅里叶变换的原理与代码实现(非调用Matlab API
[2]信号处理基础——傅里叶变换与短时傅里叶变换
[3]解析MATLAB短时傅里叶变换函数spectrogram()
[4]时频分析之短时傅里叶变换(STFT)
[5] 短时傅里叶变换(Short Time Fourier Transform)
[6] 信号处理 | 傅里叶变换、短时傅里叶变换、小波变换、希尔伯特变换、希尔伯特黄变换






